二叉树（2）

堆的应用

堆排序

首先我们先从已经学习过的冒泡排序入手：

void BubbleSort(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		int exchange = 1;
		for (int j = 0; j < n - i-1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				int tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;
				exchange = 0;
			}
		}
		if (exchange)
			break;
	}
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

通过以上代码，我们可以知道冒泡排序的时间复杂度为:O(n)=n^2，若有上万个数据需要排序时，我们就会发现该算法的效率十分慢，那么有没有更快的排序算法呢？
我们先了解上调整算法和向下调整算法的时间复杂度。

• 向上调整算法

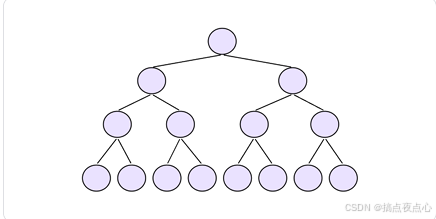
分析：
第1层，2^0个结点，需要向上移动0层
第2层，2^1个结点，需要向上移动1层
第3层，2^2个结点，需要向上移动2层
第4层，2^3个结点，需要向上移动3层
…
第h层，2^(h-1)个结点，需要向上移动h-1层
则需要移动结点总的移动步数为：每层结点个数*向上调整次数（第⼀层调整次数为0）

由此可知：向上调整算法的时间复杂度O(n)=(n∗log2 n)

• 向下调整算法

分析：
第1层，2^0个结点，需要向下移动h-1层
第2层，2^1个结点，需要向下移动h-2层
第3层，2^2个结点，需要向下移动h-3层
第4层，2^3个结点，需要向下移动h-4层
…
第h-1层，2^(h-2)个结点，需要向下移动1层
则需要移动结点总的移动步数为：每层结点个数*向下调整次数

由此可知：向下调整算法的时间复杂度O(n)=n

堆排序可由向上调整算法或向下调整算法实现：

void heapSort(int* arr,int n)
{
	//向上调整算法建堆
	for (int i = 0; i < n; i++)
	{
		AdjustUp(arr, i);
	}

	//向下调整算法建堆

	for (int j = (n - 1 - 1) / 2; j > 0; j--)
	{
		AdjustDown(arr, j, n);
	}

	int end = n - 1;
	while (end > 0)
	{
		swap(&arr[0],&arr[end]);
		AdjustDown(arr, 0, end);
		end--;
	}
	//打印
	for (int i = 0; i < 6; i++)
	{
		printf("%d ",arr[i]);
	}
	printf("\n");
}

分析：
第1层，2^0个结点，交换到根结点后，需要向下移动0层
第2层，2^1个结点，交换到根结点后，需要向下移动1层
第3层， 2^2个结点，交换到根结点后，需要向下移动2层
第4层， 2^3个结点，交换到根结点后，需要向下移动3层
…
第h层， 2^(h-1)个结点，交换到根结点后，需要向下移动h-1层

堆排序第⼆个循环中的向下调整与建堆中的向上调整算法时间复杂度计算⼀致,因此，堆排序的时间复杂度为O(n+n∗logn)，即O(n)=n∗logn

TOP-K问题（以最大为例）

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，⼀般情况下数据量都比较大。
首先创建一个函数来创造多个数据：

void CreateNDate()
{
	//造数据
	int n = 100000;
	srand(time(0));
	const char * file = "data.txt";
	FILE* fin = fopen(file, "w");
	if(fin == NULL)
	{
		perror("fopen error");
		return;
	}
	for(int i = 0; i < n; ++i)
	{
		int x = (rand() + i) % 1000000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}

思路：

1. 读取文件数据，将前k个数据存入数组中，并进行向下调整
2. 超过k个数据，则需判断，该数据是否大于数组第一个元素的大小
3. 若大于则进行交换，并向下调整

void topk()
{
	printf("请输入k:>");
	int k = 0;
	scanf("%d",&k);
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen fail!");
		exit(1);
	}
	int* minheap = (int*)malloc(sizeof(int) * k);
	if (minheap == NULL)
	{
		perror("malloc fail!");
		exit(2);
	}
	//取前k个数据
	for (int i = 0; i < k; i++)
	{
		fscanf(fout,"%d",&minheap[i]);
	}

	//建小堆
	for (int i = (k-1-1)/2; i >=0; i--)
	{
		AdjustDown(minheap,i,k);
	}
	int x = 0;
	while (fscanf(fout, "%d", &x) != EOF)
	{
		if (x > minheap[0])
		{
			minheap[0] = x;
			AdjustDown(minheap, 0, k);
		}
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ",minheap[i]);
	}
	printf("\n");
}