来想象这么一个场景:你看一群鸟儿在天上飞,它们没有头鸟带队,也没谁下命令,但它们能一起盘旋、滑翔,动作整齐划一。表面上看着乱糟糟的,实际上却井然有序。类似的现象也出现在鱼群躲避捕食者,或是蚂蚁寻找最短路径去搬食物上。这些小动物就是靠一些简单的规则和周围的沟通,就能完成那些没有中央指挥的超复杂任务。

这就是群体智能的魅力所在。
我们可以利用模仿这种群体智能的算法,来解决一些复杂的问题。
群体智能是什么?
群体智能(Swarm Intelligence) 是一种计算方法,它通过模仿自然界中鸟群或蚁群这样的群体所展现出的去中心化和自组织的行动来解决复杂的问题。
咱们来聊聊两个关键的概念:去中心化和正反馈。
去中心化和涌现现象
在群体智能里,去中心化的概念是核心。每个个体或者叫“代理”,它们不是依赖一个中心指挥来行动,而是基于自己周围的有限信息自己作决定。
这种去中心化的决策方式就带来了一种涌现的特性——就是说,复杂的、有组织的集体行为是由个体间的简单互动自然产生的。在群体智能系统里,最终的结果或者解决方案不是事先编程好的,而是从个体的行为中自然涌现出来的。
拿蚂蚁来举个例子。它们觅食的时候,会随机地探索周围环境,直到找到食物为止。找到食物后,蚂蚁会在回巢的路上留下信息素的踪迹。其他的蚂蚁如果碰到这些踪迹,就更有可能跟着走,如果它们在路的尽头找到了食物,就会加强这条路径上的信息素。时间一长,那些较短或更有效的路径就会自然地吸引更多的蚂蚁,因为这些路径上的信息素更浓。没有一只蚂蚁从一开始就“知道”最佳路线是什么,但是整个蚁群通过去中心化的决策和对成功路径的加强,最终会找到最好的解决方案。
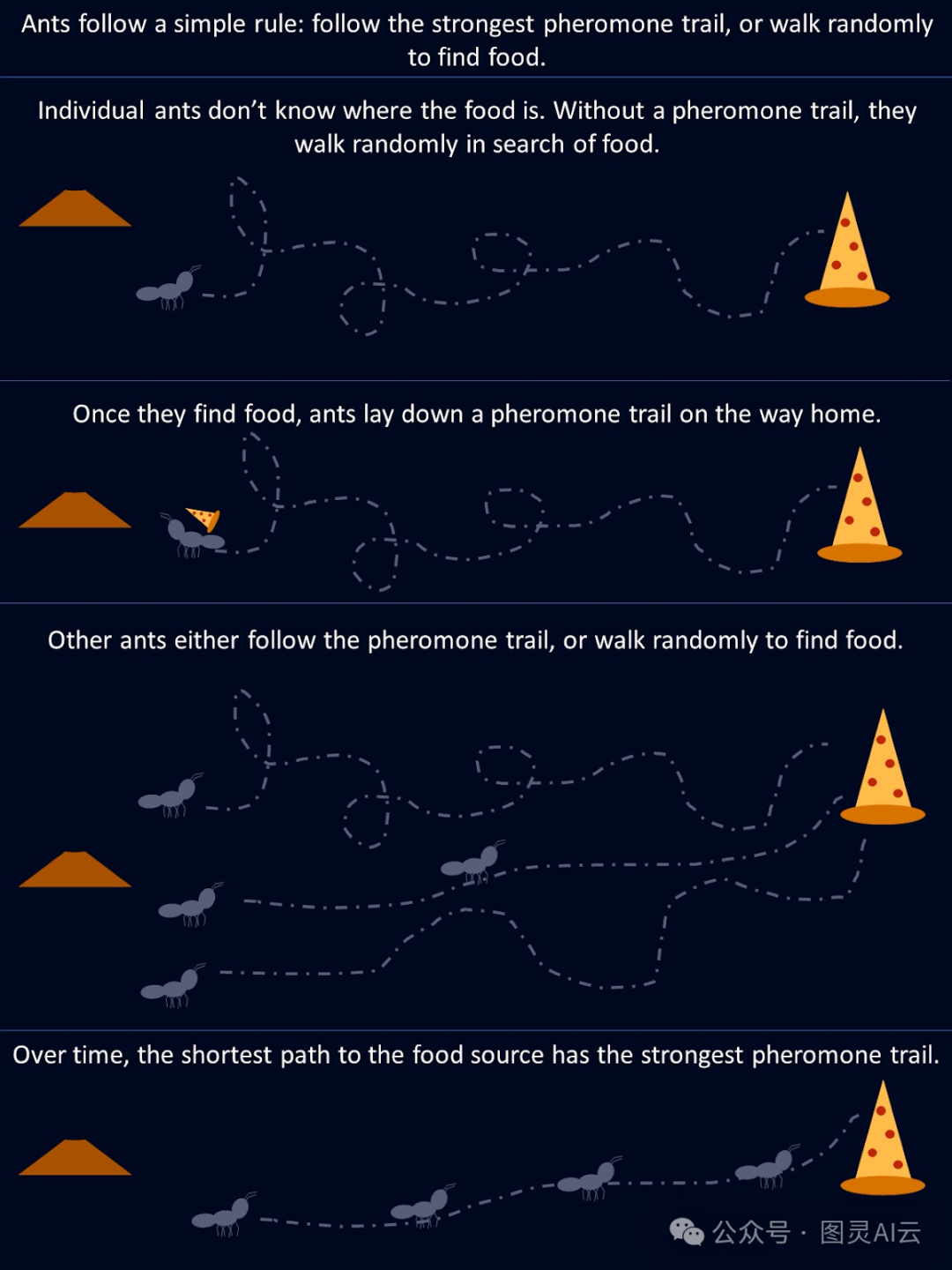
这幅图展示了个体蚂蚁遵循的简单规则如何导致整个蚁群的最优解
正反馈与适应
正反馈(Positive feedback)是群体智能系统中的一个机制,它让成功的行动得到奖励和加强。这就像一个自我放大的过程,比如蚂蚁会加强它们较短觅食路径上的信息素。这种对有益行为的加强,帮助整个群体随着时间的推移提高整体的性能。
在人工智能领域,群体智能算法通过调整关键因素(比如概率或权重)来模仿这种行为,这些调整都是基于找到的解决方案的质量。当发现更好的解决方案时,代理们会更加集中注意力在这些方案上,这加速了整个系统的收敛过程。这种动态的反馈循环让群体系统能够适应环境的变化,同时提升它们的表现。
现在,有好几种群体智能算法,它们都是模仿不同的生物系统的。我们来看看其中一些流行的算法。下面将通过使用Python实现蚁群优化(ACO)、粒子群优化(PSO)和人工蜂群(ABC),了解群体智能的工作原理。
蚁群优化(ACO)
蚁群优化(Ant Colony Optimization, ACO)是一种从蚂蚁觅食行为中得到启发的算法。它专门用来解决那些需要在众多可能的解决方案中找到最佳方案的组合优化问题。一个经典的例子就是旅行商问题,目标是找出连接一系列地点的最短路线。
蚁群优化的工作原理
在自然界,蚂蚁通过留下信息素来通信,这些信息素指示其他蚂蚁食物的方位。跟随某条路径的蚂蚁越多,那条路径上的信息素就越强。ACO通过在信息素矩阵中用数值来表示信息素,以此模仿这种行为。这个矩阵记录了不同解决方案的吸引力,并会随着算法的进行而更新。
在ACO中,每个“人工蚂蚁”代表了问题的一个潜在解决方案,比如旅行商问题中的一条可能的路线。算法开始时让所有蚂蚁随机选择路径,信息素值帮助指导蚂蚁未来的选择。这些信息素值存储在一个矩阵中,矩阵中的每个条目都对应两个点(比如城市)之间的“信息素水平”。
初始化:算法首先生成一组随机的解决方案,蚂蚁们探索不同的路径。
信息素和启发式信息:每只蚂蚁选择路径时主要受两个因素影响:信息素水平(基于之前迭代中解决方案的吸引力)和启发式信息(比如两个城市之间的距离)。信息素水平高意味着路径更可能被选中。
更新信息素:所有蚂蚁完成路径后,信息素值会更新。那些成为较好解决方案一部分的路径会得到更多的信息素加强,而那些在次优解中的路径则会有信息素的蒸发。数学上,这是通过增加矩阵中优秀解决方案的信息素值,同时减少其他路径的信息素值来实现的。
收敛:随着迭代的进行,信息素矩阵逐渐反映出最佳解决方案,引导蚂蚁们走向更优的路径。随着这个过程的重复,蚂蚁们越来越倾向于选择那些成功的路线,最终收敛到最佳解决方案。
这种信息素的数学表示让ACO能够有效地平衡探索和利用,能够在不陷入局部最优解的情况下,搜索大的解决方案空间。
蚁群优化的Python实现
我们来举一个例子,用ACO来解决一个简单的问题:在图中找到点之间的最短路径。
这个ACO的实现模拟了人工“蚂蚁”在有20个节点的图上寻找最短路径的过程。每只蚂蚁从随机的节点开始,根据信息素路径和节点间的距离来选择下一步的移动。在探索完所有可能的路径后,蚂蚁会返回到起始点,完成一个完整的循环。
随着时间的推移,信息素会得到更新:较短的路径会得到更强的加强,而其他的路径则会逐渐蒸发。这种动态的过程让算法能够收敛到最优解。
import numpy as np
import matplotlib.pyplot as plt
# Graph类代表蚂蚁将旅行的环境
class Graph:
def __init__(self, distances):
# 使用距离矩阵(节点之间的距离)初始化图
self.distances = distances
self.num_nodes = len(distances) # 节点数(城市)
# 初始化每条路径之间的信息素(与距离大小相同)
self.pheromones = np.ones_like(distances, dtype=float) # 以相等的信息素开始
# Ant类代表在图上旅行的单个蚂蚁
class Ant:
def __init__(self, graph):
self.graph = graph
# 为蚂蚁选择一个随机起始节点
self.current_node = np.random.randint(graph.num_nodes)
self.path = [self.current_node] # 用初始节点开始路径
self.total_distance = 0 # 从零开始旅行距离
# 未访问的节点是除了起始节点之外的所有节点
self.unvisited_nodes = set(range(graph.num_nodes)) - {self.current_node}
# 根据信息素和距离为蚂蚁选择下一个节点
def select_next_node(self):
# 初始化一个数组来存储每个节点的概率
probabilities = np.zeros(self.graph.num_nodes)
# 对于每个未访问的节点,根据信息素和距离计算概率
for node in self.unvisited_nodes:
if self.graph.distances[self.current_node][node] > 0: # 只考虑可达的节点
# 信息素越多,距离越短,节点被选择的可能性就越大
probabilities[node] = (self.graph.pheromones[self.current_node][node] ** 2 /
self.graph.distances[self.current_node][node])
probabilities /= probabilities.sum() # 归一化概率使其总和为1
# 根据计算出的概率选择下一个节点
next_node = np.random.choice(range(self.graph.num_nodes), p=probabilities)
return next_node
# 移动到下一个节点并更新蚂蚁的路径
def move(self):
next_node = self.select_next_node() # 选择下一个节点
self.path.append(next_node) # 添加到路径
# 将当前节点和下一个节点之间的距离加到总距离上
self.total_distance += self.graph.distances[self.current_node][next_node]
self.current_node = next_node # 更新当前节点为下一个节点
self.unvisited_nodes.remove(next_node) # 将下一个节点标记为已访问
# 通过访问所有节点并返回起始节点来完成路径
def complete_path(self):
while self.unvisited_nodes: # 当仍有未访问的节点时
self.move() # 继续移动到下一个节点
# 在访问了所有节点后,返回起始节点以完成循环
self.total_distance += self.graph.distances[self.current_node][self.path[0]]
self.path.append(self.path[0]) # 在路径的末尾添加起始节点
# ACO(蚁群优化)类运行算法以找到最佳路径
class ACO:
def __init__(self, graph, num_ants, num_iterations, decay=0.5, alpha=1.0):
self.graph = graph
self.num_ants = num_ants # 每次迭代中的蚂蚁数量
self.num_iterations = num_iterations # 迭代次数
self.decay = decay # 信息素蒸发的速率
self.alpha = alpha # 信息素更新的强度
self.best_distance_history = [] # 存储每次迭代中找到的最佳距离
# 运行ACO算法的主要函数
def run(self):
best_path = None
best_distance = np.inf # 以一个非常大的数字开始比较
# 运行指定次数的迭代算法
for _ in range(self.num_iterations):
ants = [Ant(self.graph) for _ in range(self.num_ants)] # 创建一组蚂蚁
for ant in ants:
ant.complete_path() # 让每只蚂蚁完成其路径
# 如果当前蚂蚁的路径比迄今为止找到的最佳路径短,则更新最佳路径
if ant.total_distance < best_distance:
best_path = ant.path
best_distance = ant.total_distance
self.update_pheromones(ants) # 根据蚂蚁的路径更新信息素
self.best_distance_history.append(best_distance) # 保存每次迭代的最佳距离
return best_path, best_distance
# 在所有蚂蚁完成旅行后更新路径上的信息素
def update_pheromones(self, ants):
self.graph.pheromones *= self.decay # 减少所有路径上的信息素(蒸发)
# 对于每只蚂蚁,根据它们的路径质量增加信息素
for ant in ants:
for i in range(len(ant.path) - 1):
from_node = ant.path[i]
to_node = ant.path[i + 1]
# 根据蚂蚁旅行的总距离成反比更新信息素
self.graph.pheromones[from_node][to_node] += self.alpha / ant.total_distance
# 为20个节点的图生成随机距离
num_nodes = 20
distances = np.random.randint(1, 100, size=(num_nodes, num_nodes)) # 随机距离在1到100之间
np.fill_diagonal(distances, 0) # 节点自身的距离为0
graph = Graph(distances) # 使用随机距离创建图
aco = ACO(graph, num_ants=10, num_iterations=30) # 使用10只蚂蚁和30次迭代初始化ACO
best_path, best_distance = aco.run() # 运行ACO算法以找到最佳路径
# 打印找到的最佳路径和总距离
print(f"Best path: {best_path}")
print(f"Total distance: {best_distance}")
# 绘制最终解决方案(第一张图)- 显示蚂蚁找到的最佳路径
def plot_final_solution(distances, path):
num_nodes = len(distances)
# 为节点生成随机坐标,以便在2D平面上可视化它们
coordinates = np.random.rand(num_nodes, 2) * 10
# 将节点(城市)作为红点绘制
plt.scatter(coordinates[:, 0], coordinates[:, 1], color='red')
# 用索引编号标记每个节点
for i in range(num_nodes):
plt.text(coordinates[i, 0], coordinates[i, 1], f"{i}", fontsize=10)
# 绘制连接节点的路径(边),显示找到的最佳路径
for i in range(len(path) - 1):
start, end = path[i], path[i + 1]
plt.plot([coordinates[start, 1], coordinates[end, 0]],
[coordinates[start, 0], coordinates[end, 1]],
'blue', linewidth=1.5)
plt.title("Final Solution: Best Path")
plt.show()
# 绘制迭代过程中的距离(第二张图)- 显示随着时间的推移路径长度的改善
def plot_distance_over_iterations(best_distance_history):
# 绘制每次迭代中找到的最佳距离(应该随着时间的推移而减少)
plt.plot(best_distance_history, color='green', linewidth=2)
plt.title("Trip Length Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("Distance")
plt.show()
# 调用绘图函数以显示结果
plot_final_solution(distances, best_path)
plot_distance_over_iterations(aco.best_distance_history)
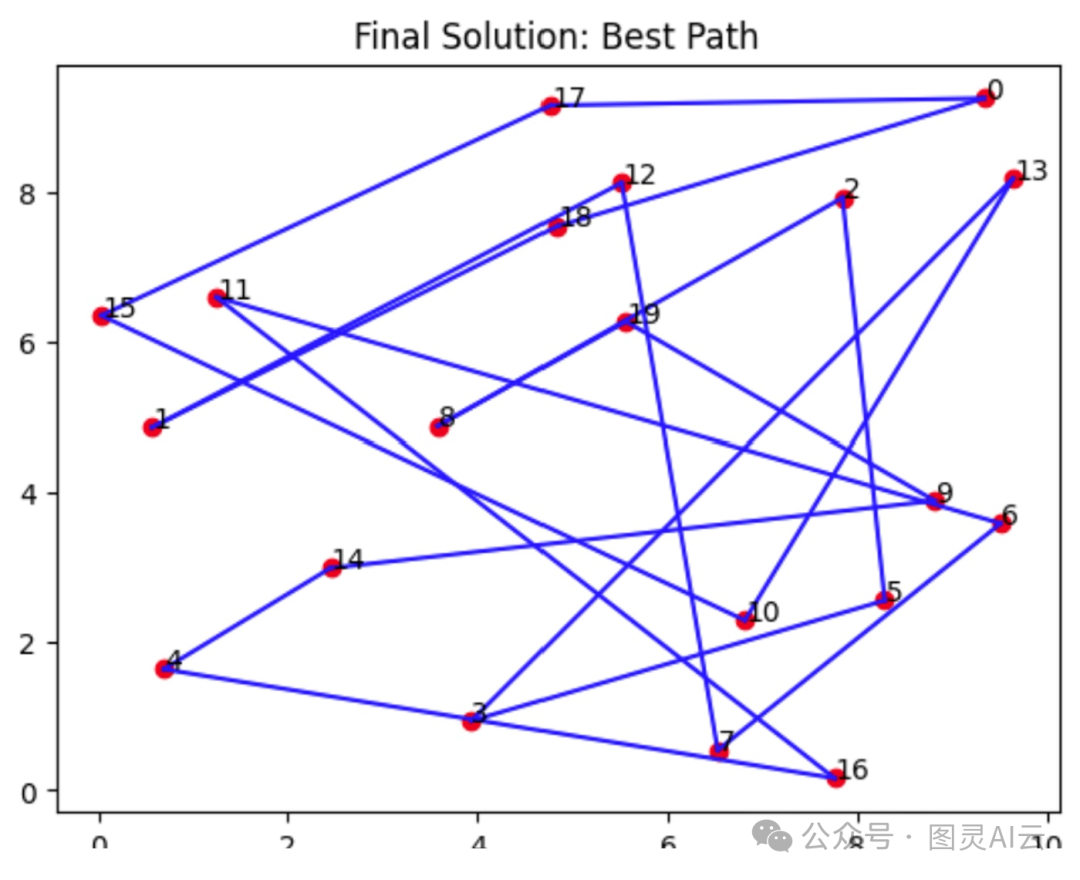
这幅图显示了最终解决方案,即找到的最短距离以访问每个节点。在这一轮中,发现的最佳路线是[4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4],总距离为129。
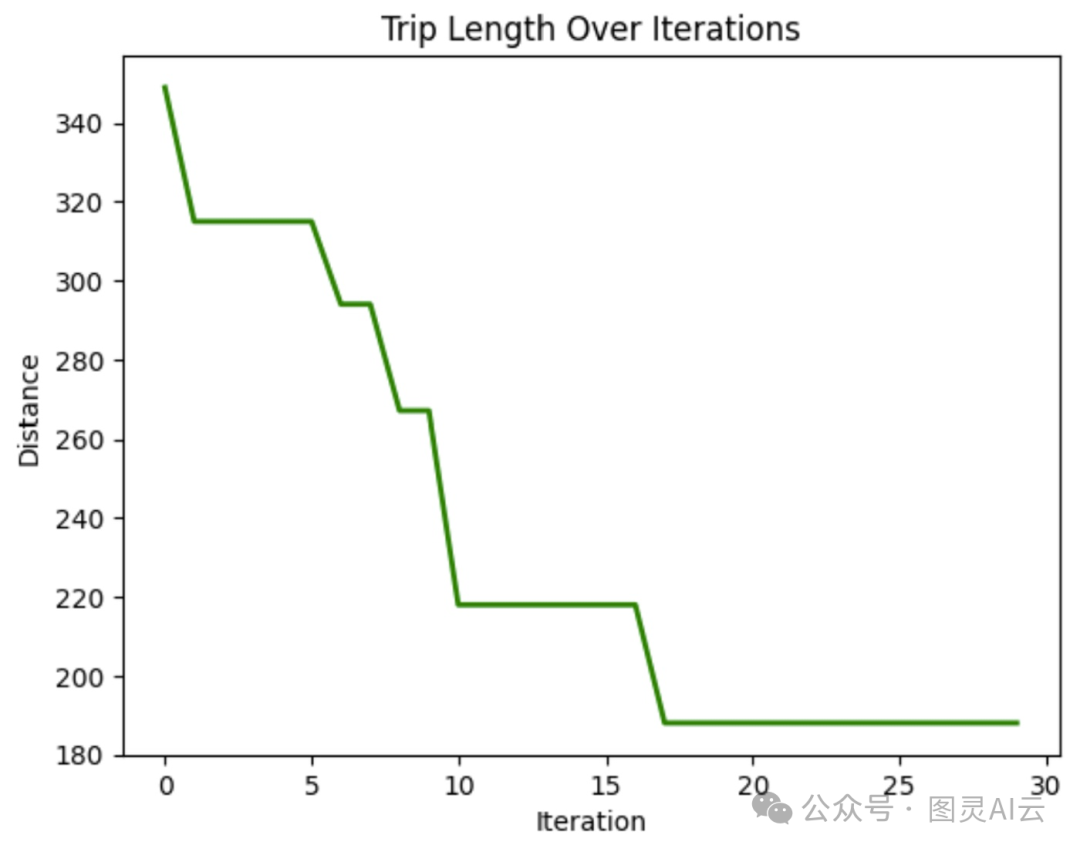
在这幅图中,我们可以看到在遍历节点时行进的距离随着迭代次数的增加而减少。这表明模型随着时间的推移改善了行程长度。
蚁群优化的应用
蚁群优化(Ant Colony Optimization, ACO) 的灵活性和效率让它在各行各业都成了一个超级有用的工具。它可以用在这些地方:
路线问题:ACO可以用来优化网络路由,比如确定数据包在网络里最短的传输路径,还有运输和快递服务。
调度:在制造或物流领域,ACO也能派上用场,比如在任务调度上,确保资源分配得当。
资源分配:这个算法还能用来分配那些有限的资源,比如在项目管理或者需要同时考虑多个变量的复杂操作中。
ACO的厉害之处在于它能够进化和适应,这让它在需要实时变化的环境里,比如实时交通路线规划或者工业规划,都能大显身手。
粒子群优化(PSO)
粒子群优化(Particle Swarm Optimization, PSO) 是从鸟群和鱼群的行为中得到的灵感。在这些自然界的系统中,每个个体会根据自己的经验和邻居的位置来移动,慢慢调整自己去跟随群体里最成功的那些成员。PSO把这一套应用到了优化问题上,里面的粒子,也就是代理,会在搜索空间里寻找那个最优解。
和ACO不一样,PSO是在连续的空间而不是离散的空间里工作。在ACO里,我们关注的是路径查找和做出离散的选择,而PSO更适合处理有连续变量的问题,比如调整参数。
在PSO里,粒子们会去探索这个搜索空间。它们调整自己的位置,主要是基于两个因素:它们自己已知的最佳位置,以及整个群体已知的最佳位置。这种双重反馈的机制,让粒子们能够集中到全局的最优解上去。
粒子群优化的工作原理
这个过程是从在解决方案空间里随机分布的一群粒子开始的。每个粒子都代表了优化问题的一个可能的解决方案。粒子在移动的时候,会记下自己的最佳位置——就是它们到目前为止遇到的最好的解决方案,同时也会向全局最佳位置靠拢——也就是任何粒子找到的最好的解决方案。
这种移动是由两个东西推动的:一个是利用,就是围绕当前已知的最佳解决方案进行更精细的搜索;另一个是探索,就是鼓励粒子去搜索解决方案空间的其他部分,避免被困在局部的最优解里。通过平衡这两种动作,PSO能够有效地集中到最佳的解决方案上去。
粒子群优化Python实现
在金融投资组合管理中,要找到那种能够带来最大回报同时又把风险降到最低的资产分配方式,可能会挺复杂的。我们可以用PSO来找找哪种资产组合能给我们带来最高的投资回报。
下面这段代码就展示了PSO是怎么用来优化一个虚构的金融投资组合的。它从随机的资产分配开始,然后在几次迭代中根据效果进行调整,慢慢地就能找到那种能够带来最高回报和最低风险的最佳资产组合。
import numpy as np
import matplotlib.pyplot as plt
# 定义PSO参数
class Particle:
def __init__(self, n_assets):
# 使用随机权重和速度初始化粒子
self.position = np.random.rand(n_assets)
self.position /= np.sum(self.position) # 归一化权重,使它们总和为1
self.velocity = np.random.rand(n_assets)
self.best_position = np.copy(self.position)
self.best_score = float('inf') # 以一个非常高的分数开始
def objective_function(weights, returns, covariance):
"""
计算投资组合的性能。
- weights:投资组合中的资产权重。
- returns:资产的预期回报。
- covariance:表示风险的协方差矩阵。
"""
portfolio_return = np.dot(weights, returns) # 计算投资组合回报
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(covariance, weights))) # 计算投资组合风险(标准差)
return -portfolio_return / portfolio_risk # 我们希望最大化回报并最小化风险
def update_particles(particles, global_best_position, returns, covariance, w, c1, c2):
"""
更新每个粒子的位置和速度。
- particles:粒子对象列表。
- global_best_position:所有粒子找到的最佳位置。
- returns:资产的预期回报。
- covariance:表示风险的协方差矩阵。
- w:惯性权重,控制粒子先前速度的影响。
- c1:认知系数:粒子从自己的最佳解决方案中学到多少。
- c2:社会系数:粒子从全局最佳解决方案中学到多少。
"""
for particle in particles:
# 速度更新的随机系数
r1, r2 = np.random.rand(len(particle.position)), np.random.rand(len(particle.position))
# 更新速度
particle.velocity = (w * particle.velocity +
c1 * r1 * (particle.best_position - particle.position) +
c2 * r2 * (global_best_position - particle.position))
# 更新位置
particle.position += particle.velocity
particle.position = np.clip(particle.position, 0, 1) # 确保权重在0和1之间
particle.position /= np.sum(particle.position) # 归一化权重使其总和为1
# 评估新位置
score = objective_function(particle.position, returns, covariance)
if score < particle.best_score:
# 更新粒子的最佳已知位置和分数
particle.best_position = np.copy(particle.position)
particle.best_score = score
def pso_portfolio_optimization(n_particles, n_iterations, returns, covariance):
"""
执行粒子群优化以找到最优资产权重。
- n_particles:群体中的粒子数量。
- n_iterations:优化的迭代次数。
- returns:资产的预期回报。
- covariance:表示风险的协方差矩阵。
"""
# 初始化粒子
particles = [Particle(len(returns)) for _ in range(n_particles)]
# 初始化全局最佳位置
global_best_position = np.random.rand(len(returns))
global_best_position /= np.sum(global_best_position)
global_best_score = float('inf')
# PSO参数
w = 0.5 # 惯性权重:粒子受自身方向影响的程度
c1 = 1.5 # 认知系数:粒子从自己的最佳解决方案中学习的效果
c2 = 0.5 # 社会系数:粒子从全局最佳解决方案中学习的效果
history = [] # 存储每次迭代的最佳分数
for _ in range(n_iterations):
update_particles(particles, global_best_position, returns, covariance, w, c1, c2)
for particle in particles:
score = objective_function(particle.position, returns, covariance)
if score < global_best_score:
# 更新全局最佳位置和分数
global_best_position = np.copy(particle.position)
global_best_score = score
# 存储最佳分数(负回报/风险比率)以供绘图
history.append(-global_best_score)
return global_best_position, history
# 示例数据,用于3种资产
returns = np.array([0.02, 0.28, 0.15]) # 每种资产的预期回报
covariance = np.array([[0.1, 0.02, 0.03], # 资产风险的协方差矩阵
[0.02, 0.08, 0.04],
[0.03, 0.04, 0.07]])
# 运行PSO算法
n_particles = 10 # 粒子数量
n_iterations = 10 # 迭代次数
best_weights, optimization_history = pso_portfolio_optimization(n_particles, n_iterations, returns, covariance)
# 绘制优化过程
plt.figure(figsize=(12, 6))
plt.plot(optimization_history, marker='o')
plt.title('Portfolio Optimization Using PSO')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value (Negative of Return/Risk Ratio)')
plt.grid(False) # 关闭网格线
plt.show()
# 显示最优资产权重
print(f"Optimal Asset Weights: {best_weights}")Was this helpful?
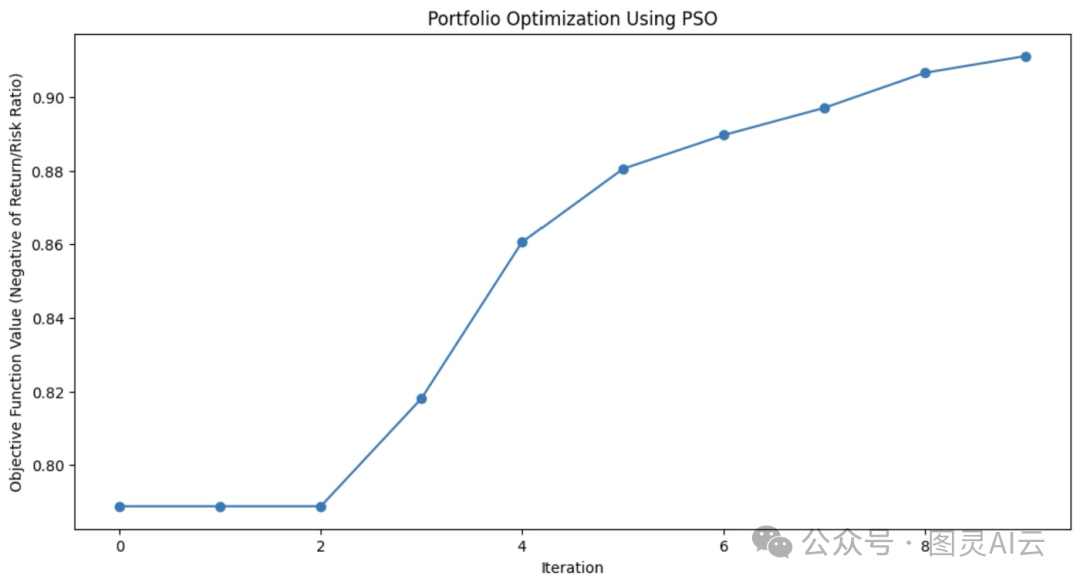
这幅图展示了PSO算法在每次迭代中如何改进投资组合的资产组合
粒子群优化的应用
粒子群优化(PSO)因为它简单又有效,被广泛用于解决各种优化问题,特别是在需要处理连续变量的情况下。它的灵活性让它在很多需要精确解决方案的真实场景中都能大显身手。
PSO的应用包括但不限于:
机器学习:PSO可以用来调整机器学习算法的超参数,帮助我们找到最佳的模型配置。
工程设计:PSO也能帮助优化像航空部件或电子电路这类系统的设计参数。
金融建模:在金融领域,PSO能助力投资组合的优化,让我们在最小化风险的同时,最大化回报。
PSO能有效探索解决方案的空间,这使得它在机器人技术、能源管理、物流等多个领域都能派上用场。
人工蜂群(ABC)
人工蜂群(Artificial Bee Colony, ABC) 算法是模仿蜜蜂觅食行为的一种建模方法。
在自然界,蜜蜂非常高效地寻找花蜜源,并且会和其他蜂巢成员分享这些信息。ABC算法就是捕捉这种协作搜索的过程,并将其应用于解决优化问题,特别是那些涉及复杂、高维空间的问题。
和其他群体智能算法相比,ABC的特别之处在于它平衡了利用和探索的能力,专注于改进当前的解决方案,同时也探索新的、可能更好的解决方案。这让ABC在需要全局优化的大型问题上特别有效。
人工蜂群的工作原理
在ABC算法中,蜂群被分成三个专业的角色:工蜂、观察蜂和侦察蜂。每个角色都模拟了蜜蜂在自然界中寻找和利用食物源的不同方面。
工蜂:这些蜜蜂负责探索已知的食物源,相当于优化问题中的当前解决方案。它们会评估这些源的质量(适应度),并和其他蜂巢成员分享这些信息。
观察蜂:在收集了工蜂的信息之后,观察蜂会选择哪些食物源值得进一步探索。它们的选择基于工蜂分享的解决方案的质量,更多地关注那些更好的选项,从而细化寻找最优解决方案的过程。
侦察蜂:当一个工蜂的食物源(解决方案)变得不再有价值或者停滞不前(比如在一定次数的迭代后没有改进)时,这只蜜蜂就会变成侦察蜂。侦察蜂会去探索解决方案空间的新区域,寻找那些可能还没被探索的食物源,为搜索过程带来多样性。
这种动态平衡让ABC能够在深入探索有希望的区域和广泛探索新区域之间保持平衡。这有助于算法避免陷入局部最优解,并且增加了找到全局最优解的机会。
人工蜂群Python实现
Rastrigin函数是优化问题中的一个经典问题,它因为有很多局部最小值而闻名,给很多算法都带来了挑战。我们的目标很简单:找到全局最小值。
在这个例子中,我们将使用人工蜂群算法来解决这个问题。ABC算法中的每只蜜蜂都在搜索空间中寻找更好的解决方案来最小化这个函数。代码模拟了探索、利用和侦察新区域的蜜蜂,确保了探索和利用之间的平衡。
import numpy as np
import matplotlib.pyplot as plt
# Rastrigin函数:目标是最小化这个函数
def rastrigin(X):
A = 10
return A * len(X) + sum([(x ** 2 - A * np.cos(2 * np.pi * x)) for x in X])
# 人工蜂群(ABC)算法,用于连续优化Rastrigin函数
def artificial_bee_colony_rastrigin(n_iter=100, n_bees=30, dim=2, bound=(-5.12, 5.12)):
"""
应用人工蜂群(ABC)算法最小化Rastrigin函数。
参数:
n_iter(int):迭代次数
n_bees(int):种群中的蜜蜂数量
dim(int):维度(变量)数量
bound(tuple):搜索空间的界限(最小值,最大值)
返回值:
tuple:找到的最佳解决方案、最佳适应度值,以及每次迭代的最佳适应度值列表
"""
# 使用给定界限内随机解决方案初始化蜜蜂种群
bees = np.random.uniform(bound[0], bound[1], (n_bees, dim))
best_bee = bees[0]
best_fitness = rastrigin(best_bee)
best_fitnesses = []
for iteration in range(n_iter):
# 工蜂阶段:基于当前蜜蜂探索新的解决方案
for i in range(n_bees # 通过扰动当前蜜蜂的位置生成一个新的候选解决方案
new_bee = bees[i] + np.random.uniform(-1, 1, dim)
new_bee = np.clip(new_bee, bound[0], bound[1]) # 保持在界限内
# 评估新解决方案的适应度
new_fitness = rastrigin(new_bee)
if new_fitness < rastrigin(bees[i]):
bees[i] = new_bee # 如果新解决方案更好,则更新蜜蜂
# 观察蜂阶段:利用好的解决方案
fitnesses = np.array([rastrigin(bee) for bee in bees])
probabilities = 1 / (1 + fitnesses) # 更高的适应度获得更高的机会
probabilities /= probabilities.sum() # 归一化概率
for i in range(n_bees):
if np.random.rand() < probabilities[i]:
selected_bee = bees[i]
# 通过扰动选择的蜜蜂生成一个新的候选解决方案
new_bee = selected_bee + np.random.uniform(-0.5, 0.5, dim)
new_bee = np.clip(new_bee, bound[0], bound[1])
if rastrigin(new_bee) < rastrigin(selected_bee):
bees[i] = new_bee
# 侦察阶段:随机重新初始化一些蜜蜂以探索新区域
if np.random.rand() < 0.1: # 10%的机会重新初始化蜜蜂
scout_index = np.random.randint(n_bees)
bees[scout_index] = np.random.uniform(bound[0], bound[1], dim)
# 跟踪迄今为止找到的最佳解决方案
current_best_bee = bees[np.argmin(fitnesses)]
current_best_fitness = min(fitnesses)
if current_best_fitness < best_fitness:
best_fitness = current_best_fitness
best_bee = current_best_bee
best_fitnesses.append(best_fitness)
return best_bee, best_fitness, best_fitnesses
# 应用ABC最小化Rastrigin函数
best_solution, best_fitness, best_fitnesses = artificial_bee_colony_rastrigin()
# 显示结果
print("Best Solution (x, y):", best_solution)
print("Best Fitness (Minimum Value):", best_fitness)
# 绘制每次迭代的性能
plt.figure()
plt.plot(best_fitnesses)
plt.title('Performance of ABC on Rastrigin Function Optimization')
plt.xlabel('Iterations')
plt.ylabel('Best Fitness (Lower is Better)')
plt.grid(True)
plt.show()
# 绘制Rastrigin函数的表面图
x = np.linspace(-5.12, 5.12, 200)
y = np.linspace(-5.12, 5.12, 200)
X, Y = np.meshgrid(x, y)
Z = 10 * 2 + (X ** 2 - 10 * np.cos(2 * np.pi * X)) + (Y ** 2 - 10 * np.cos(2 * np.pi * Y))
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar(label='Function Value')
plt.scatter(best_solution[0], best_solution[1], c='red', label='Best Solution')
plt.title('Rastrigin Function Optimization with ABC')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
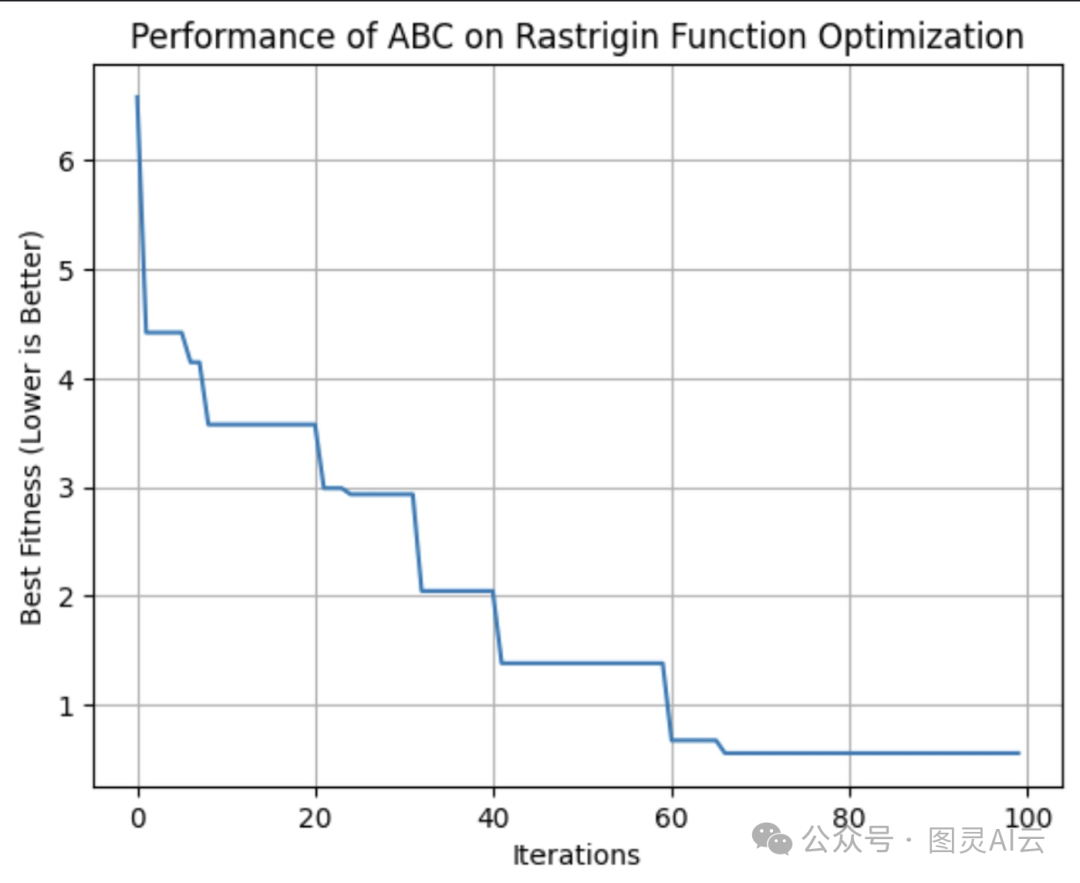
这幅图展示了ABC算法在每次迭代中找到的最佳解决方案的适应度,在这一轮中,它在第64次迭代时达到了最佳适应度
这里可以看到Rastrigin函数的轮廓图,显示了许多局部最小值。红点是我们运行的ABC算法找到的全局最小值。
人工蜂群的应用
人工蜂群(ABC)算法是个优化问题的超强工具。它在探索大规模和复杂的搜索空间时效率特别高,这让它在需要快速适应和扩展的行业中特别受欢迎。
它的应用范围很广,包括:
电信:可以用ABC来优化网络资源和天线的布局,这样就能在覆盖范围和信号强度上做到最好,同时还能节省成本。
工程:在结构设计中,ABC也可以用来调整参数,以达到最优设计。
数据科学:在特征选择方面,ABC可以帮助我们识别出对机器学习模型最重要的数据特征。
ABC算法的灵活性和去中心化的特性让它在需要动态、高维空间中寻找最优解的问题上表现得特别好。
比较群体智能算法
有很多种群体智能算法,每种都有它自己的特点。选择哪种算法时,需要根据它们各自的优缺点来决定哪个最适合你的需求。
蚁群优化(ACO)在解决组合问题,比如路由和调度时很有效,但可能会需要很多计算资源。
粒子群优化(PSO)更简单,适合连续优化问题,比如超参数调整,但可能会陷入局部最优解。
人工蜂群(ABC)成功地平衡了探索和利用,虽然它需要仔细调整参数。
其他群体智能算法,比如萤火虫算法(Firefly Algorithm, FA)和杜鹃搜索(Cuckoo Search Optimization, CS),也为特定类型的优化问题提供了独特的优势。
| 算法 | 优势 | 劣势 | 优选库 | 最佳应用 |
|---|---|---|---|---|
| 蚁群优化(ACO) | 适合解决组合问题,能处理复杂离散空间 | 计算密集型,需要精细调优 | pyaco | 路由问题、调度和资源分配 |
| 粒子群优化(PSO) | 适合连续优化,简单易实现 | 可能收敛到局部最优解,对离散问题效果较差 | pyswarms | 超参数调优、工程设计、金融建模 |
| 人工蜂群(ABC) | 适应大规模动态问题,平衡探索和利用 | 计算密集型,需要仔细的参数调优 | beecolpy | 电信、大规模优化和高维空间 |
| 萤火虫算法(FA) | 在多模态优化中表现优异,全局搜索能力强 | 对参数设置敏感,收敛速度较慢 | fireflyalgorithm | 图像处理、工程设计和多模态优化 |
| 杜鹃搜索(CS) | 解决优化问题效率高,探索能力强 | 可能过早收敛,性能依赖于调优 | cso | 调度、特征选择和工程应用 |
挑战与限制
群体智能算法和其他机器学习技术一样,也面临着可能影响其性能的挑战,比如:
过早收敛:群体可能太快就停在了次优解上。
参数调优:要得到最佳结果,通常需要仔细调整算法的设置。
计算资源与可扩展性:这些算法可能很耗计算资源,特别是在处理更大、更复杂的问题时,随着问题复杂性的增加,性能可能会下降。
随机性:算法的随机性可能导致结果的可变性。
最新研究与进展
一个明显的趋势是将群体智能与其他机器学习技术结合起来。研究人员正在探索群体算法如何增强特征选择和超参数优化等任务,比如这篇论文《用于解决工程问题的混合粒子群优化算法》(https://www.nature.com/articles/s41598-024-59034-2.pdf)。
近期的研究进展也在集中解决群体智能的传统挑战,比如过早收敛。新的算法和技术正在开发中,以减少收敛到次优解的风险,比如这篇论文《基于记忆的方法消除粒子群优化中的过早收敛》(https://link.springer.com/article/10.1007/s10489-020-02045-z)。
可扩展性也是一个重要的研究领域。随着问题变得越来越复杂,数据量不断增加,研究人员正在努力使群体智能算法更具可扩展性和效率,包括开发能够更有效处理大数据集和高维空间的算法,同时优化计算资源,以减少运行这些算法所需的时间和成本,比如这篇综述《群体搜索的理论和适用性的最新发展》(https://www.mdpi.com/1099-4300/25/5/710)。
群体算法正在被应用于从机器人技术到大型语言模型(LLMs)到医学诊断的各种问题。正在进行的研究还在探讨这些算法是否可以帮助LLMs在遵守“被遗忘权”法规时有策略地忘记信息。当然,群体算法在数据科学中也有广泛的应用。
结论
群体智能为各行业的优化问题提供了强大的解决方案。其去中心化、正反馈和适应性的原则使其能够处理传统算法可能难以应对的复杂动态任务。
你可以查看这篇综述《群体智能:模型分类与应用的调查》(https://www.sciencedirect.com/science/article/pii/S1000936124000931)来了解更多关于群体智能算法当前状态的信息。
