始终致力于将复杂知识通俗化的不断追求中,不足之处欢迎批评指正。
1、噪声处理
噪声是一个测量变量中的随机错误或偏差,是观测值和真实值之间的误差,包括错误值或偏离期望的孤立点值。对于噪声的处理,通常可以采用数据平滑技术来消除噪声。下面将介绍几种数据平滑技术。
(1)分箱
分箱方法通过考察数据的“邻居”(即周围的数据值)来平滑数据。在这种方法中,首先对数据进行排序,然后将排序后的值分配到多个“桶”或“箱”中,即分箱。由于分箱方法参考邻居的值,所以它进行的是局部平滑。
如何对数据进行分箱?下面介绍两种基本的分箱方法。
(1)等宽(距)法
将数据值从最小值到最大值分成具有相同宽度的K个区间(箱),K由数据特点决定,往往是需要有业务经验的人进行评估。假设某个属性的最小值表示为Min,最大值表示为Max,箱的个数为K,则箱宽(W)的计算公式为:
箱宽(W)= (Max - Min)/K
因此,第i个区间的范围可以表示为[Min+(i-1)W,Min+iW) ],其中i=1,2,3……K。
例如,对数据集[5,10,11,13,15,35,50,55,72,92,204,215],设置分箱数为3,一共分成三个区间。按照等宽分箱的方式来划分,箱宽=(215-5)/3=70,因此,数据被划分为[5,75)、[75,145)、[145,215],等宽分箱的结果为:
Bin1=[5,10,11,13,15,35,50,55,72] , Bin2=[92], Bin3=[204,215]
(2)等深(频)法
等深法是试图在每个区间放同样个数的元素,使得每个区间大致包含相同个数的临近数据样本。将属性值分为具有相同深度的区间,区间K根据实际情况来决定。比如有60个样本,我们要将其分为K=3部分,则每部分的长度为20个样本。在等深法中,先将数据进行排序,然后计算K个分位点来确定每个区间的左右边界。
采用等宽法中的数据集,等深分箱的结果为:
Bin1=[5, 10, 11, 13],Bin2=[15, 35, 50, 55],Bin3=[72, 92, 204, 215]
每个区间中都含有相同数目的样本,即4个样本。
如何使用分箱结果对数据进行平滑处理?有三种方法可以执行平滑:
1)按箱平均值光滑:箱中每一个值被箱中的平均值替换;
2)按箱中位数平滑:箱中的每一个值被箱中的中位数替换;
3)按箱边界平滑:箱中的最大和最小值被视为边界。箱中的每一个值被最近的边界值替换。
价格的排序后数据(美元):2,6,7,9,13,20,21,25,30。使用等深方法进行划分,划分后的结果为:Bin1=[2,6,7],Bin2=[9,13,20],Bin3=[21,24,30]。不同方法执行数据平滑后的结果如表所示。

2、数据变换
数据变换是指将数据从一种表示形式变为另一种表现形式的过程,目标是将数据转换为更适合于挖掘的形式。常见的数据变换可能涉及如下内容:
☛属性构造:根据给定属性中构造新的属性,或者将属性类别进行变换,辅助数据挖掘过程。
由给定的属性构造和添加新的属性,以帮助数据分析和挖掘过程。例如,我们可以根据“高度”属性和“宽度”属性,构造一个新的“面积”属性。通过组合属性,可以将属性之间的关联信息用一个属性来表示,这对知识发现是有用的。
☛规范化:将属性数据按比例缩放,使之落入一个特定的区间,如[-1,1]或者[0,1],以便消除属性之间的量纲和取值范围差异的影响。
规范化主要是因为数据中不同属性的量纲可能不一致,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果。因此,需要对数据按照一定比例进行缩放,使之落在一个特定的区域,便于进行综合分析。特别是基于距离的挖掘方法,例如,K-均值,K-近邻,支持向量机等,一定要做规范化处理。
常用的规范化的方法有总和规范化、Z-Score规范化、最小-最大规范化、极大值规范化和对数变换。假设数据变量j的数据样本数为m,X_j={x_1j,x_2j, x_3j,…,x_mj },各规范化方法的定义如下:
(1)总和规范化
总和规范化处理后的数据值之和为1。总和规范化的公式如下所示:

(2)Z-Score规范化
Z-Score规范化使用原始数据的均值(Mean)和标准差(Standard Deviation)进行数据的规范化,同时不改变原始数据的分布。它可以去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。Z-Score规范化的公式如下所示:

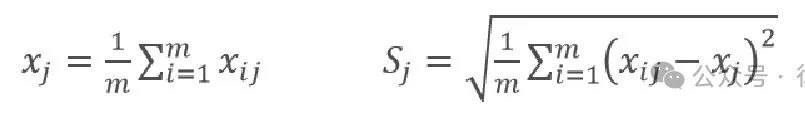
✔原理 :通过“减均值,除标准差”,将数据转换为均值为0、标准差为1的分布。
✔公式 :(原始值 - 平均值) ÷ 标准差
✔例子 :
某次考试平均分70,标准差10,小明考了80分。
规范化后:(80-70)/10 = 1 → 表示小明比平均分高1个标准差。
如果数据中有离群点,对数据进行Z-Score标准化效果并不好,这时可以由中位数(Median)取代平均值,用平均绝对离差(AAD)或中值绝对离差(MAD)取代标准差来修正。
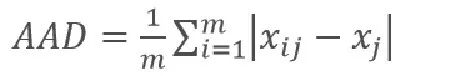
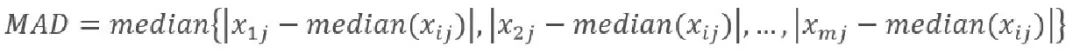
其中,AAD是数据与均值距离的平均值,MAD是数据与中位数距离的中位数。
(3)最小-最大规范化
最小-最大规范化的公式:
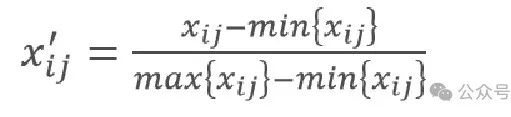
✔原理 :将数据缩放到一个固定范围(如0到1之间)。
✔公式 :(原始值 - 最小值) ÷ (最大值 - 最小值)
✔例子 :
某天气温范围是20℃到30℃。25℃规范化后:(25-20)/(30-20) = 0.5 → 表示处于中间位置。用途 :适用于需要统一量纲的场景(比如图像像素值归一化)
经过最小-最大规范化处理后的新数据,各元素的最大值为1,最小值为0,其余数值均在0与1之间,即将数据缩放到[0,1]范围内。这里的min{x_ij}和max{x_ij}指的是和x_ij同一列的最小值和最大值。
(4)极大值规范化
极大值规范化的公式:
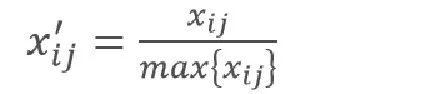
✔原理 :直接用每个数除以最大值,让最大值变为1,其他数小于1。
✔公式 :原始值 ÷ 最大值
✔例子 :
某商品价格为100元、200元、500元。
规范化后:0.2、0.4、1 → 最大值500元变为1。
✔用途 :快速压缩数据范围,但对异常值敏感。
极大值规范化后的新数据的最大值为1,其余各项都小于1。
(5)对数变换规范化
公式所示的对数变换能够缩小数据的绝对范围,其目的是它能够让变换后的数据符合所做的假设(比如服从正态分布),从而能够运用已有理论上对其进行分析。
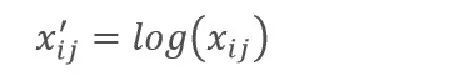
✔原理 :用对数函数缩小数据范围,让数据更接近正态分布。
✔公式 :log(原始值) 或 ln(原始值)
✔例子 :
某城市人口增长率为1000、10000、100000。
取对数后(以10为底):3、4、5 → 数据差异被压缩。
✔用途 :处理指数级增长的数据(如收入、人口)。