核心概念
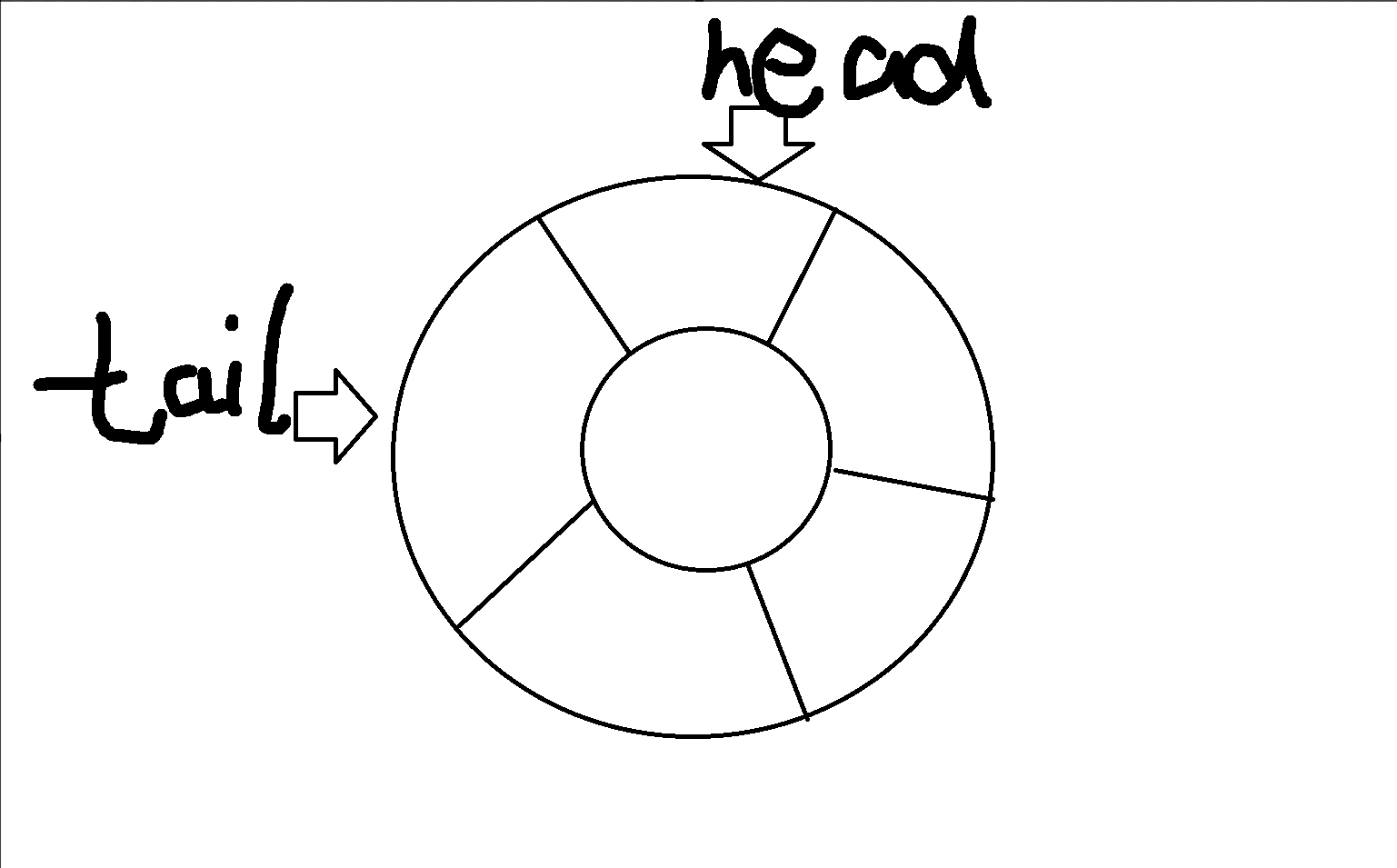
循环队列(Circular Queue),也称为环形队列,是一种特殊的队列数据结构。它通过将队列的首尾相连,解决了传统队列因出队操作导致的空间浪费问题(即“假溢出”),从而更高效地利用固定大小的内存空间。
 =
=
传统队列的问题:
- 普通队列基于数组实现时,一旦队尾指针(
tail)到达数组末尾,即使队列头部有空闲位置,也无法再插入新元素,导致空间无法复用。 - 例如:数组大小为5,队列经过多次入队和出队后,可能出现头部有空位,但尾部已满的情况,无法继续入队。
- 普通队列基于数组实现时,一旦队尾指针(
循环队列的解决方案:
- 将数组的逻辑首尾相连,形成一个环。
- 通过模运算(
%)控制队首(head)和队尾(tail)指针的移动,使其在到达数组末尾后能回到起始位置,重复利用空间。
关键特性
核心指针:
head:指向队列的第一个元素。tail:指向下一个可插入元素的位置。
关键操作:
- 入队(Enqueue):向队尾插入元素,
tail指针后移。 - 出队(Dequeue):从队首移除元素,
head指针后移。
- 入队(Enqueue):向队尾插入元素,
空和满的判定:
- 队列空:
head == tail且count == 0。 - 队列满:
head == tail且count == capacity(通过计数器实现,无需浪费空间)。
(传统方法可能用(tail + 1) % capacity == head判断队列满,但会浪费一个位置)
- 队列空:
实现原理
1. 指针移动规则
- 入队时:
tail = (tail + 1) % capacity - 出队时:
head = (head + 1) % capacity
2. 元素数量计算
- 通过
count变量直接记录当前元素数量,无需依赖head和tail的位置关系。 - 元素数量:
count = (tail - head + capacity) % capacity(未使用count时)。
3. 空间复用
- 当指针移动到数组末尾时,通过模运算回到数组头部,形成一个逻辑上的“环”。
示例分析
假设队列容量为5,初始状态如下:
head = 0, tail = 0, count = 0,数组为 [ , , , , ]。
入队4个元素(62, 84, 26, 89):
head=0,tail=4,count=4,队列为[62,84,26,89, ]。- 打印结果:
62<-84<-26<-89。
继续入队45:
vec[4] = 45,tail = 0,count=5,队列已满。- 队列为
[62,84,26,89,45],打印结果:62<-84<-26<-89<-45。
尝试入队46:
- 队列已满,操作失败。
出队一次:
head=1,count=4,队列为[ ,84,26,89,45]。- 打印结果:
84<-26<-89<-45。
优缺点
优点:
- 高效利用固定内存空间,避免假溢出。
- 入队和出队的时间复杂度均为 O(1)。
- 适用于需要严格限制内存的场景(如嵌入式系统、实时系统)。
缺点:
- 需要预先分配固定大小,扩容困难。
- 空和满的判定需谨慎处理,容易出错。
应用场景
- 缓冲区管理:如键盘输入缓存、网络数据包缓冲。
- 任务调度:操作系统中的进程就绪队列。
- 生产者-消费者模型:多线程环境下高效传递数据。
- 循环任务队列:如打印机任务队列、消息队列。
STL(标准模板库)中没有直接提供固定容量的循环队列(Circular Queue)实现,但可以通过组合现有容器(如 vector 或 deque)及索引管理来模拟循环队列的特性。以下是具体说明和实现示例:
使用vector底层容器实现
通过 vector 存储元素,并用 head 和 tail 索引标记队列的起止位置,利用模运算实现循环。
这个程序实现了一个循环队列(cirqueue),使用C++的模板类和vector作为底层容器。以下是对程序的详细分析:
程序结构
主函数(文档1):
- 创建容量为5的整型循环队列。
- 连续入队4个元素(62, 84, 26, 89),打印队列。
- 继续尝试入队45(成功)和46(失败,队列已满),再次打印。
- 执行一次出队操作,打印最终队列。
循环队列实现(文档2):
- 使用
vector存储元素,维护head(队首索引)、tail(下一个插入位置)、count(当前元素数量)和capacity(队列容量)。 - 提供
enqueue(入队)、dequeue(出队)、isempty(判空)和printqueue(打印队列)方法。
- 使用
核心逻辑分析
1. 构造函数
explicit cirqueue(size_t capacity) : vec(capacity), head(0), tail(0), count(0), capacity(capacity) {}- 初始化
vector大小为capacity,元素默认初始化(对于int可能为未定义值)。 head和tail初始为0,count记录当前元素数量。
2. 入队操作(enqueue)
void enqueue(T text) {
if (count == capacity) {
cout << "" << endl; // 应输出明确提示,如"Queue is full"
return;
}
vec[tail] = text;
tail = (tail + 1) % capacity;
count++;
}- 队列满条件:
count == capacity。 - 元素插入到
tail位置,tail循环后移。 - 当队列满时,拒绝新元素并输出空提示(需改进)。
3. 出队操作(dequeue)
void dequeue() {
if (count == 0) {
cout << "" << endl; // 应输出明确提示,如"Queue is empty"
return;
}
head = (head + 1) % capacity;
count--;
}- 队列空条件:
count == 0。 - 移动
head指针,不实际删除元素,仅减少count。
4. 打印队列(printqueue)
void printqueue() {
for (auto i = 0; i < count; ++i) {
auto k = (i + head) % capacity;
cout << vec[k];
if (i != count - 1) cout << "<-";
}
cout << endl;
}- 按逻辑顺序(从
head开始)遍历count个元素,用<-连接。
主函数执行流程
初始状态:
head=0,tail=0,count=0,capacity=5.vector初始值为未定义的int(可能为随机值)。
四次入队(62, 84, 26, 89):
tail依次移动到4,count=4。- 打印结果:
62<-84<-26<-89。
第五次入队(45):
vec[4] = 45,tail=0,count=5(队列满)。- 打印结果:
62<-84<-26<-89<-45。
第六次入队(46):
- 队列已满,操作失败,无提示(需改进)。
一次出队:
head移动到1,count=4。- 打印结果:
84<-26<-89<-45。
主函数测试
#include"cirqueue.h"
int main() {
cirqueue<int>que(5);
que.enqueue(62);
que.enqueue(84);
que.enqueue(26);
que.enqueue(89);
que.printqueue();
que.enqueue(45);
que.enqueue(46);
que.printqueue();
que.dequeue();
que.printqueue();输出结果:

deque为底层容器实现
通过限制 deque 的最大容量并在队列满时删除旧元素:
#include <deque>
template<typename T>
class FixedSizeQueue {
public:
explicit FixedSizeQueue(size_t max_size) : max_size(max_size) {}
void push(T value) {
if (dq.size() == max_size) {
dq.pop_front(); // 满时删除队首
}
dq.push_back(value);
}
// 其他接口与 std::queue 类似
private:
std::deque<T> dq;
size_t max_size;
};性能对比
| 实现方式 | 入队/出队时间复杂度 | 内存连续性 | 是否支持动态扩容 |
|---|---|---|---|
基于 vector |
O(1) | 连续 | 否 |
基于 deque |
O(1) | 分段连续 | 否(手动限制) |
boost::circular_buffer |
O(1) | 连续 | 是 |
如何选择?
- 需要严格内存控制:用
vector+ 环形索引(方法 1)。 - 需要动态扩容:使用
boost::circular_buffer。 - 简单场景:基于
deque手动限制容量(方法 2)。
如果追求 STL 的纯粹性,推荐自己实现方法 1;若允许使用第三方库,直接采用 Boost 的实现更高效且功能完整。