本篇文章主要是讲解经典的排序算法 -- 归并排序
目录
1 递归版本的归并排序
1) 算法思想
归并排序与快速排序相同,都是运用了分治算法思想:将规模为 n 的问题分为k个规模较小的与原问题性质一致且相互独立的子问题,然后解决各个子问题,将子问题的解合并为大问题的解。
归并排序是利用了之前合并两个有序链表的思想,每次将大问题二分,直到分到只有一个元素的子数组的情况,将只含有一个元素的子数组看作是一个有序的子数组,然后再合并两个有序数组,这样子问题就解决了,解决每一个子问题之后,大问题也就随之解决了。下面是解决两个个子问题的算法过程(这里假设排升序):
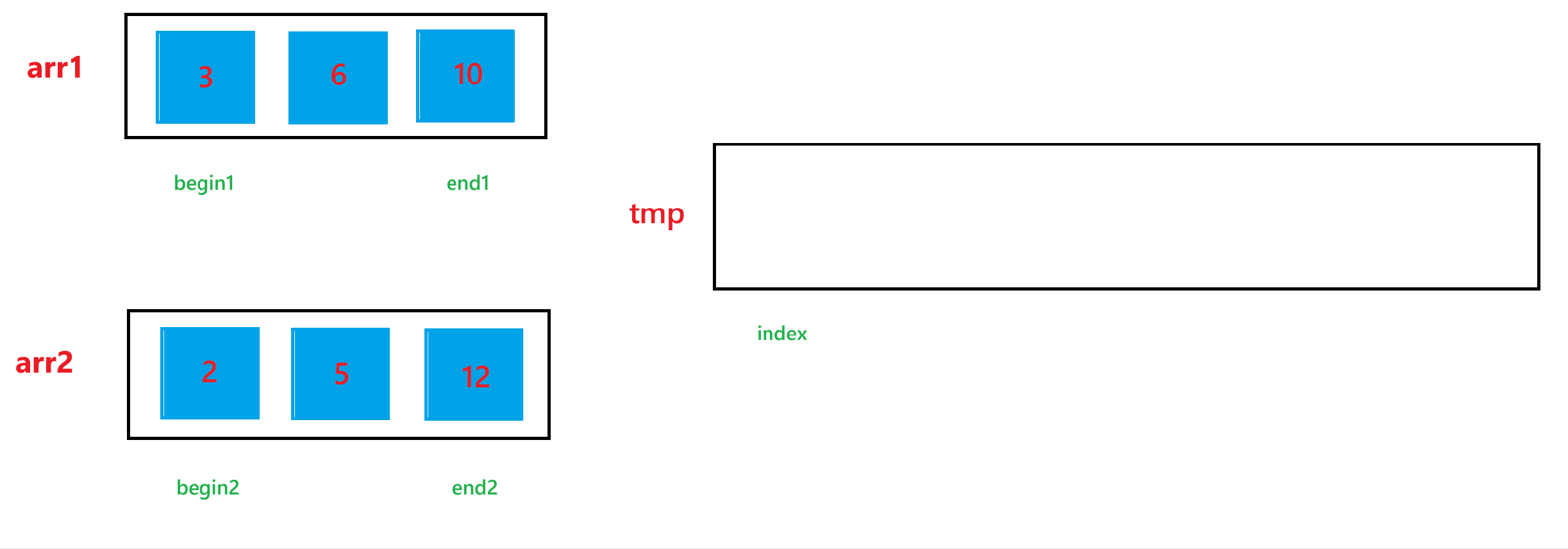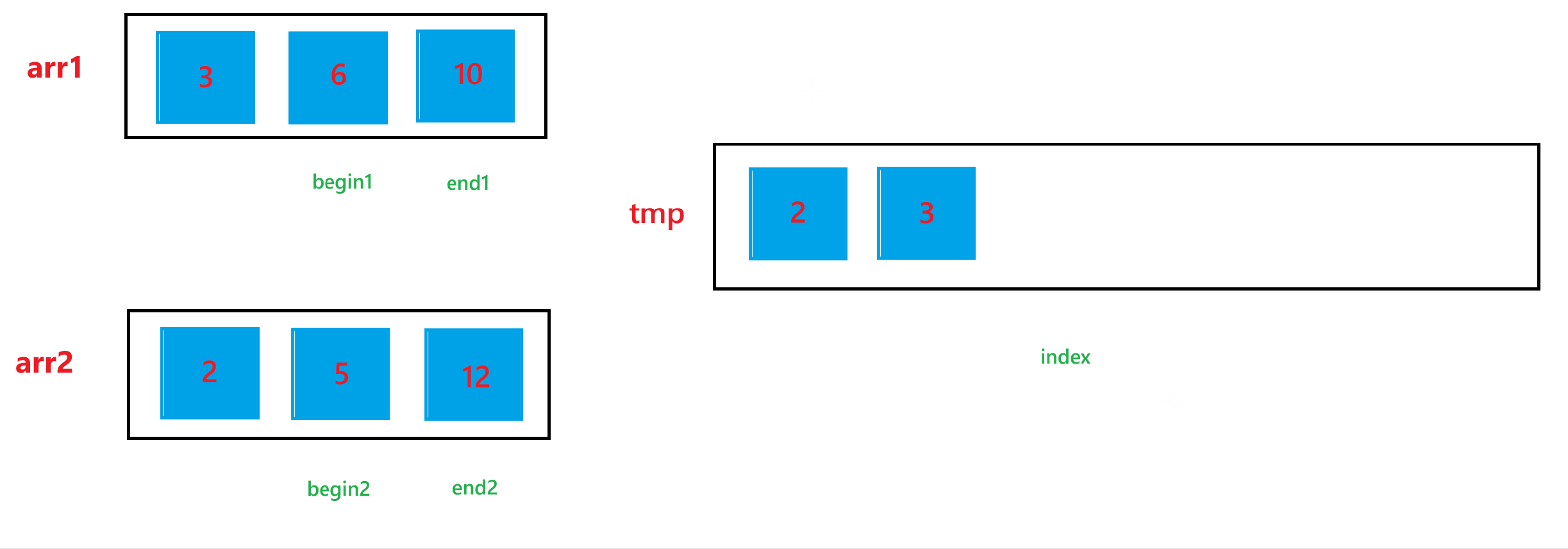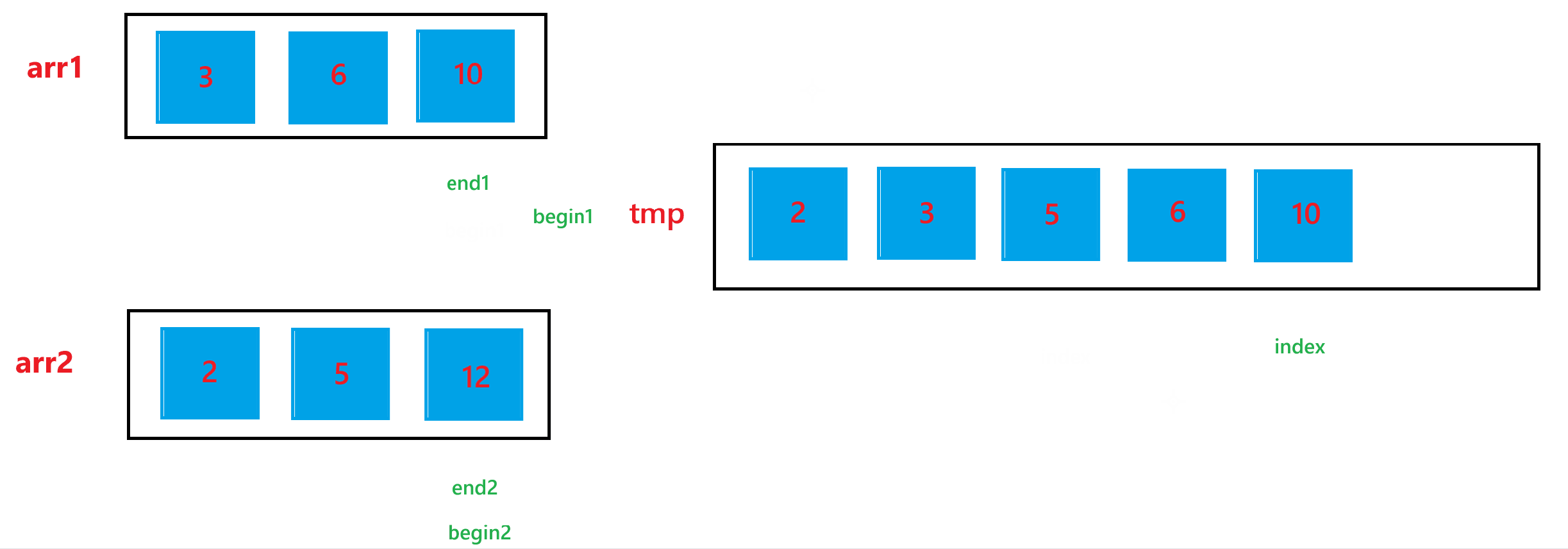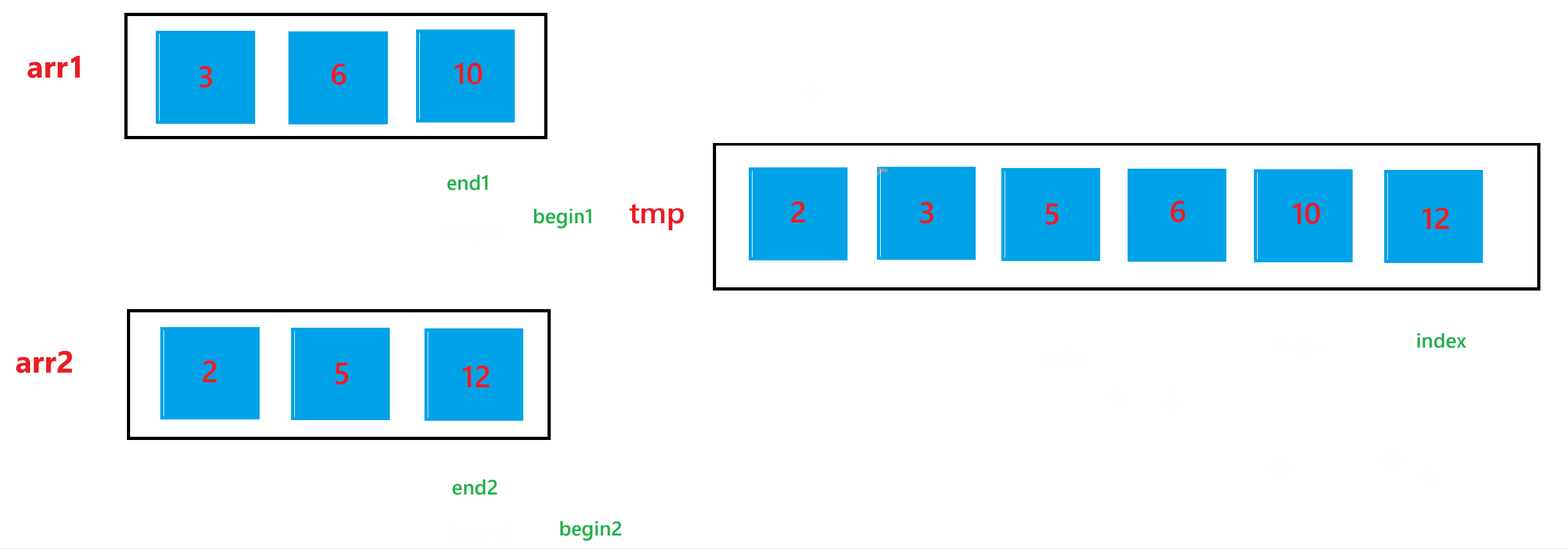
a. 首先定义 4 个整型变量 begin1, end1, begin2, end2, 这里假设要排序的整个数组为 arr,其中一个子问题,也就是要合并的第一个有序数组为 arr1;另一个子问题,也就是要合并的第二个有序数组为 arr2。begin1 与 begin2 分别指向 arr1 和 arr2 的起始下标,end1 与 end2 分别指向 arr1 和 arr2 的结束下标,合并两个有序数组还需要一个中间数组 tmp 以及一个整型变量 index,tmp 来暂时存储合并两个有序数组后的结果,index 用来表示 tmp 数组当前存储结果的下标。
b. 然后依次比较 arr1[begin1] 与 arr2[begin2] 的大小关系,如果 arr1[begin1] < arr2[begin2] ,那就让 tmp[index] = arr1[begin1],然后 ++index,++begin1;否则,就让 tmp[index] = arr2[begin2],然后 ++index,++begin2。循环上述过程,直到 begin1 > end1 或者 begin2 > end2。
c. 经历过第二步之后,arr1 与 arr2 肯定会有一个数组还有元素,我们需要把剩下的元素也放到 tmp 里面,所以如果 begin1 <= end1,就让 tmp[index] = arr1[begin1],然后 ++index,++begin1;如果 begin2 <= end2,就让 tmp[index] = arr2[begin2],然后 ++index,++begin2。
d. 经历过上述两步之后,arr1 与 arr2 的合并结果已经放到 tmp 数组中了,最后不要忘记让合并后的结果,也就是 tmp 中的元素要放回排序的数组 arr 中。
下面是合并合并两个有序数组的过程:
下面是归并排序划分子问题的过程:

注意上述过程只是描述了递归划分子问题的过程,没有进行合并,原则上是当划分到每一条绿色的竖线左右两边子数组只有一个元素的时候,就应该进行合并了。
2) 代码
归并排序主函数:
void MergeSort(int* arr,int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail!\n");
exit(1);
}
_MergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}归并排序子函数:
void _MergeSort(int* arr, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = left + (right - left) / 2;
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
//合并两个有序数组
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
tmp[index++] = arr[begin1++];
else
tmp[index++] = arr[begin2++];
}
while (begin1 <= end1)
tmp[index++] = arr[begin1++];
while (begin2 <= end2)
tmp[index++] = arr[begin2++];
//再将tmp数组的内容放回arr数组
for (int i = left;i <= right;i++)
arr[i] = tmp[i];
}解释: 归并排序主函数的作用主要是动态开辟一个辅助数组 tmp 与释放动态开辟的空间,防止内存泄漏,tmp 主要用来帮助完成有序数组的合并;在子函数里面,left 代表要进行排序的子数组的最左边元素的下标,right 代表要进行排序的子数组的最右边元素的下标;然后开始有一个递归的边界条件,当 left >= right,也就是子数组中只有一个元素或者没有元素的时候,就会停止递归,此时将只有一个元素的子数组视为是一个有序数组;边界条件下面的三行代码主要就是用来进行递归,划分子问题的,首先计算出大问题的中间位置下标 mid,然后将大问题在中间数组划分为两个子问题,也就是对 [left, mid] 与 [mid + 1, right] 区间的数组进行递归;再后面的代码就是为了解决某两个具体的子问题也就是合并两个有序数组的过程(上面已经讲解过,这里不再赘述)。
测试用例:
int main()
{
int arr[] = { 10, 2, 5, 7, 1, 4, 8, 9, 6, 20};
int n = sizeof(arr) / sizeof(arr[0]);
MergeSort(arr, n);
Print(arr, n);
return 0;
}3) 时间复杂度与空间复杂度分析
(1) 时间复杂度
与快速排序相同,带有递归的函数的时间复杂度计算包括两部分,一部分是解决子问题的时间复杂度,另一部分是递归的深度,T(n) = 递归深度 * 解决子问题的时间复杂度。
我们先来看解决子问题的时间复杂度,看上面解决具体解决子问题的代码,由于只有一层循环,且循环的次数最多是 end1 - begin1 或者 end2 - begin2 次,最坏情况下是对最开始要排序的整个数组从中间划分的两个子数组进行排序的时候,此时循环的次数就是 n / 2 次,所以解决子问题的时间复杂度 T(n) = O(n)。
再来看递归的深度,由于每次都对数组进行二分,在中间位置划分数组,对左边数组进行递归,再对右边数组进行递归,所以递归树应该为:

我们假设最开始的数组元素个数为 n,那么递归到第二层的时候每个子数组元素个数就为 n/2,第三层就为 n/4,也就是 n/2^2,第四层就是 n/2^3,所以递归到第 x 层的时候元素个数就为 n/2^x,而递归的停止条件为元素个数为 1,所以 n/2^x = 1 ==> x = ,所以总的层数应该是
+ 1 层,所以递归的深度为
+ 1。
所以归并排序的时间复杂度 T(n) = O(nlogn + n) ==> T(n) = O(nlogn)。
(2) 空间复杂度
由于在函数中使用了一个辅助数组 tmp 来帮助合并,其余都是有限的变量,所以空间复杂度 S(n) = O(n)。
2 迭代版本的归并排序
1) 算法思想
在迭代版本的归并排序中,我们依然可以借助递归版本归并排序的算法思想:先将数组划分到 1 个元素的子数组的情况,将 1 个元素的子数组看作是有序的数组,然后依次合并两个有序数组,最终使数组有序;在迭代版本归并排序中,我们划分子问题是用一个 gap 变量来实现的,具体过程如下:
a. 函数会传入两个参数:arr(数组元素首地址)与 n (数组元素个数),先创建一个整型变量 gap 与一个辅助数组 tmp(用来合并两个有序数组);开始先让 gap = 1,代表每个要合并的数组里只有一个元素,之后每次循环都让 gap *= 2,代表要合并的数组由 1 个元素变为 2 个元素,之后再变为 4 个元素,依次类推,直到 gap >= n,就停止排序。
b. 然后在每次循环里面,由于在大数组里我们要寻找要合并的两个子数组,所以我们还要用一个变量 i 来遍历数组,寻找要合并的两个子数组;在循环过程中,i 每次会指向要合并的两个子数组中第一个子数组的首元素,由于每次首次要合并的第一个子数组总是以 0 下标元素开头的子数组,所以 i 总是以 0 开头,然后合并完两个有序子数组之后,i 会指向下一次要合并的两个有序子数组的第一个子数组首元素,所以 i 在遍历过程中会跳过上一次排序的两个子数组,也就是 2 * gap 个元素,即 i += 2 * gap;停止条件也很简单,就是 i >= n 越界时,就会停止两个子数组的合并。
c. 在合并两个子数组的过程中需要找到两个子数组,这里用 begin1, end1 代表第一个要合并的子数组的起始和结束位置,begin2 和 end2 代表第二个要合并的子数组的起始和结束位置,根据 i 与 gap 就可以推算出 begin1、end1、begin2、与 end2:begin1 = i,end1 = i + gap - 1,begin2 = i + gap,end2 = begin1 + gap - 1 = i + 2 * gap - 1。
d. 再创建一个 index 来记录要放到 tmp 数组中的位置,开始先让 index = begin1,之后进行两个有序数组的合并(上面递归版本讲解过,这里不再赘述),最后不要忘记让 tmp 中的元素放到 arr 数组中。
当 gap = 1 时排序过程如图所示: 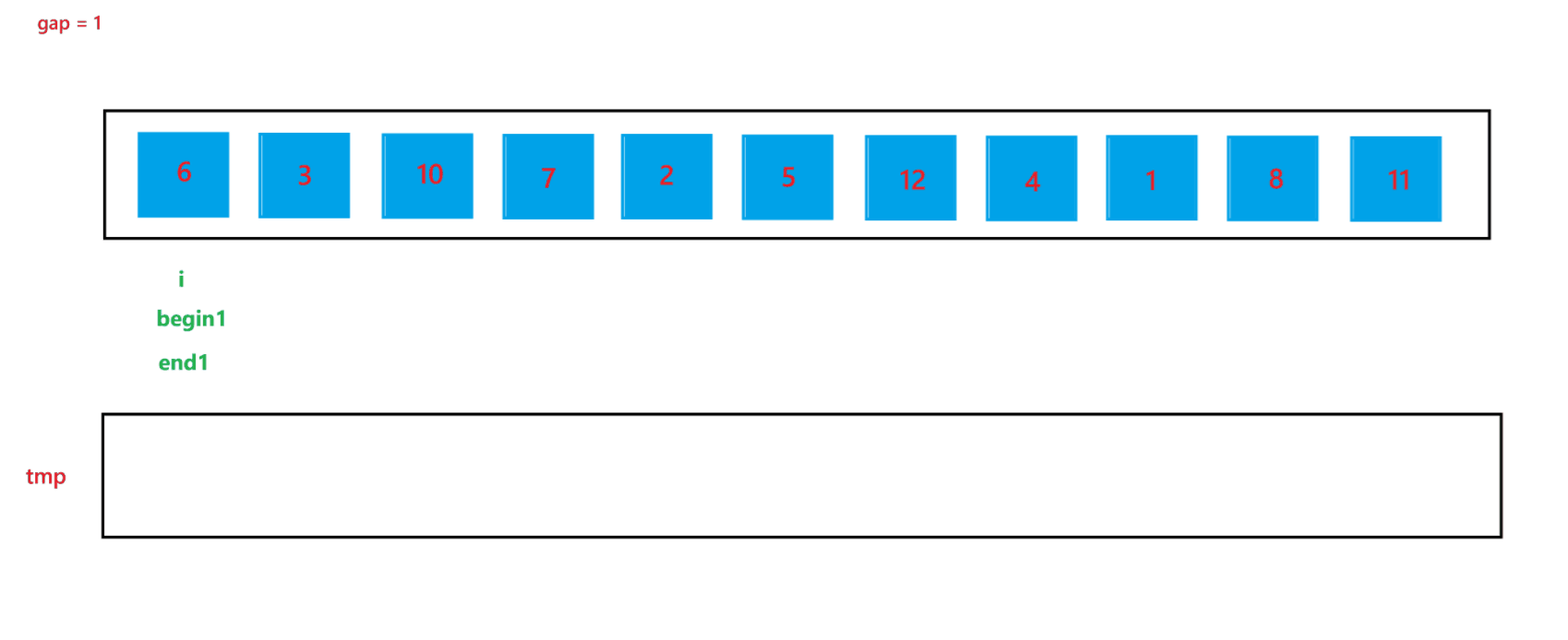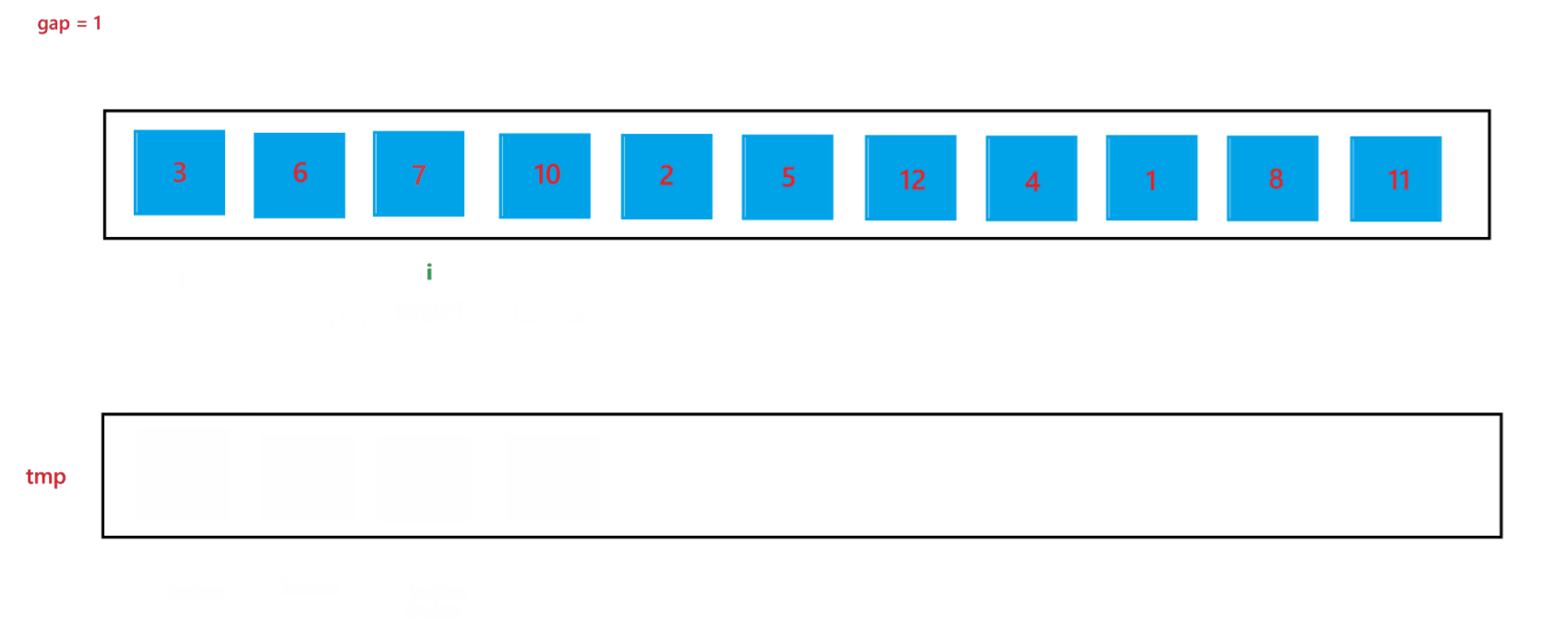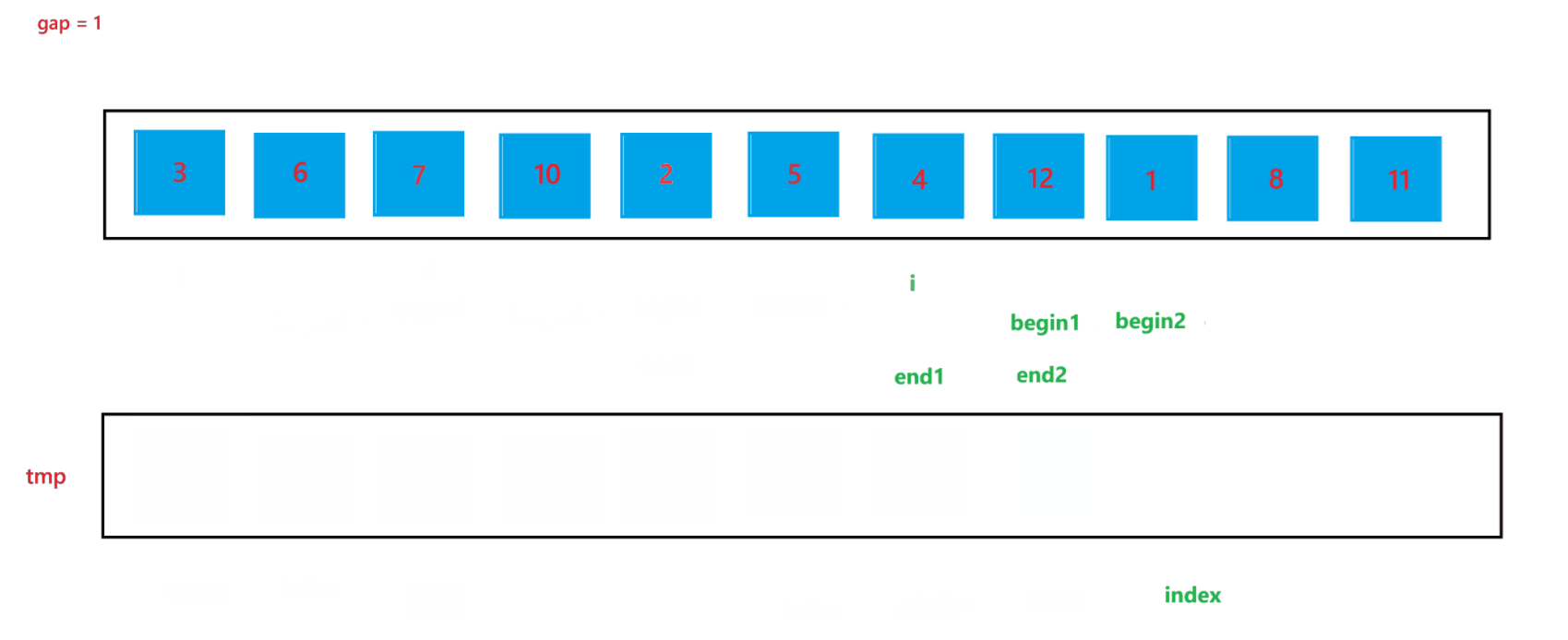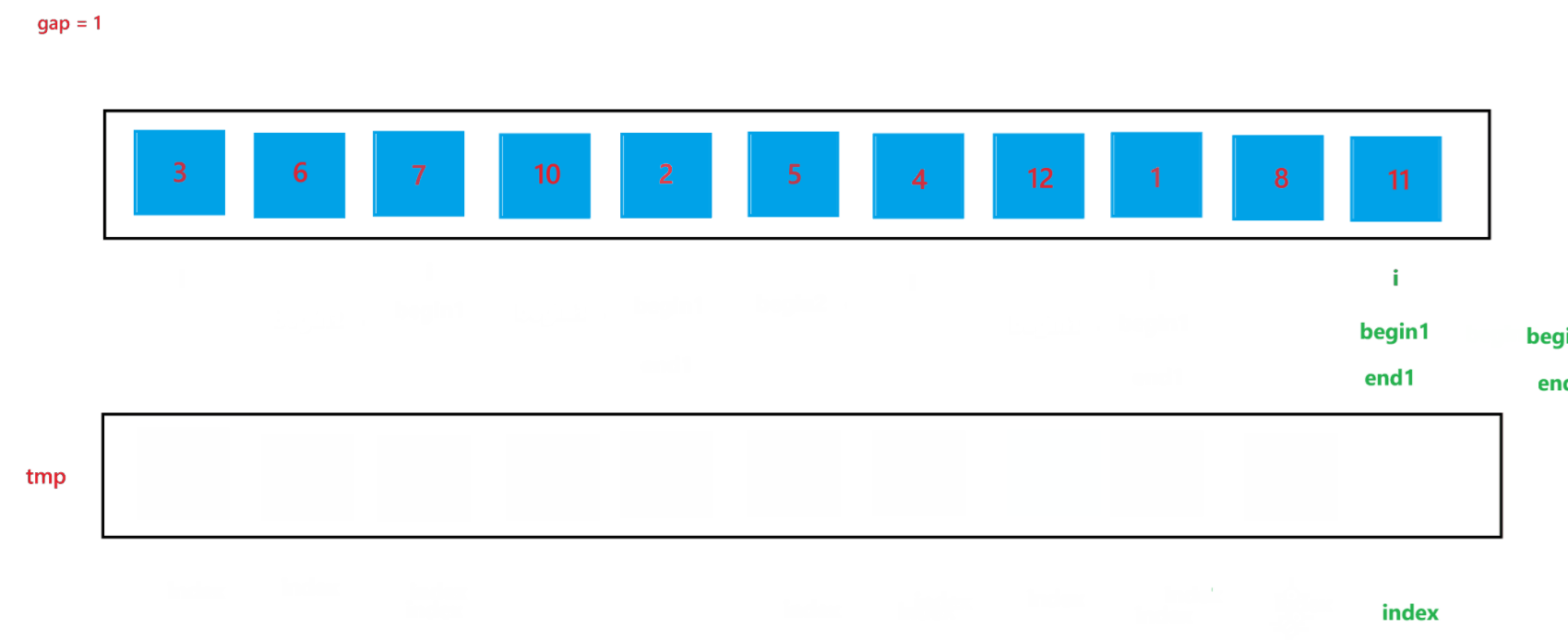
在上述的合并过程中,我们可以发现 begin2 与 end2 是可能发生越界的,所以当发生越界情况时,我们需要特殊处理一下:当 begin2 越界时,此时代表 begin1 的子数组后面是没有 begin2 子数组与其合并的,也就是此时只有一个有序子数组,就代表此次不需要合并了,跳出循环即可;当end2 越界时,会在 gap = 2 中出现,下面我们再详细讨论。
当 gap = 2 时排序过程如图所示:
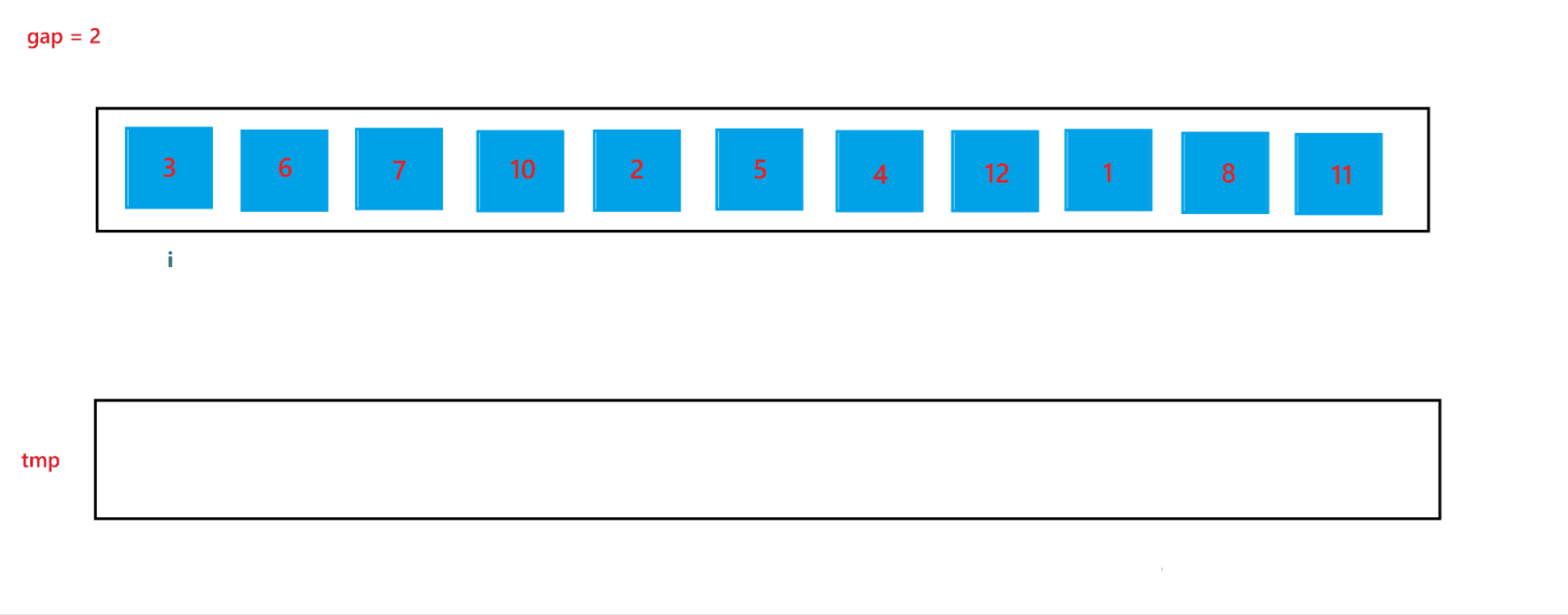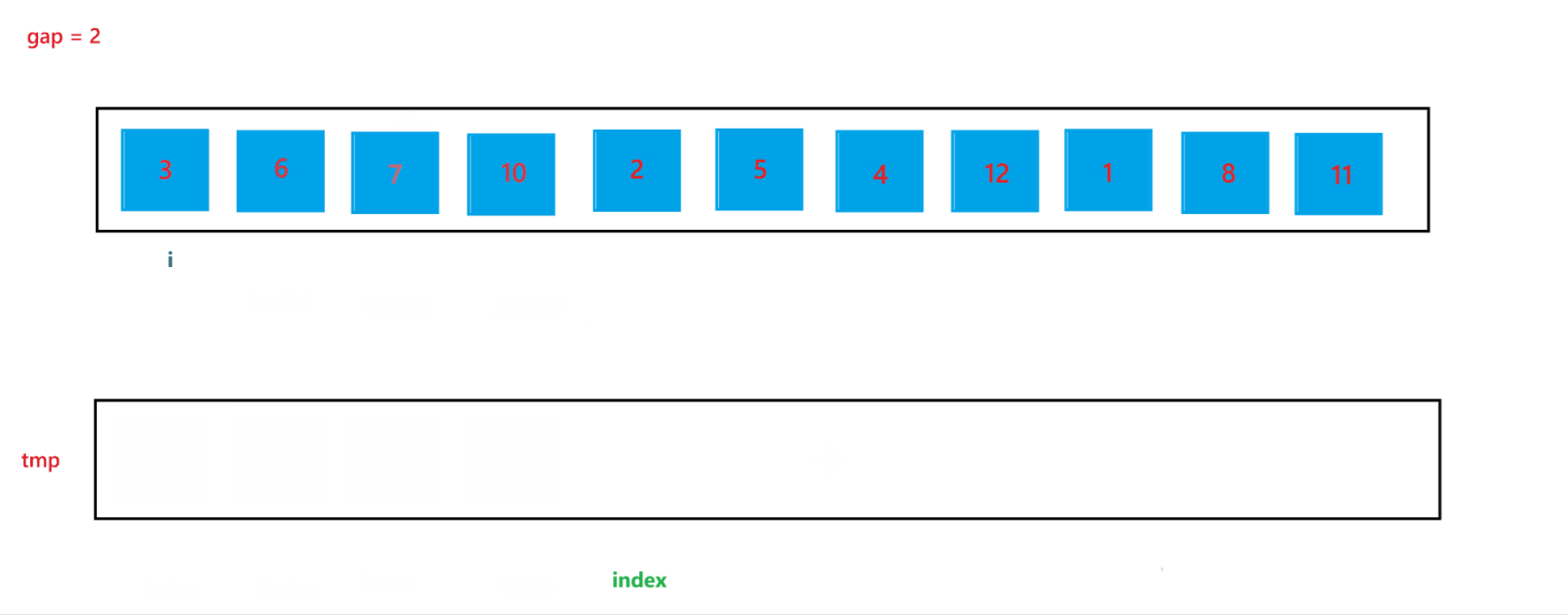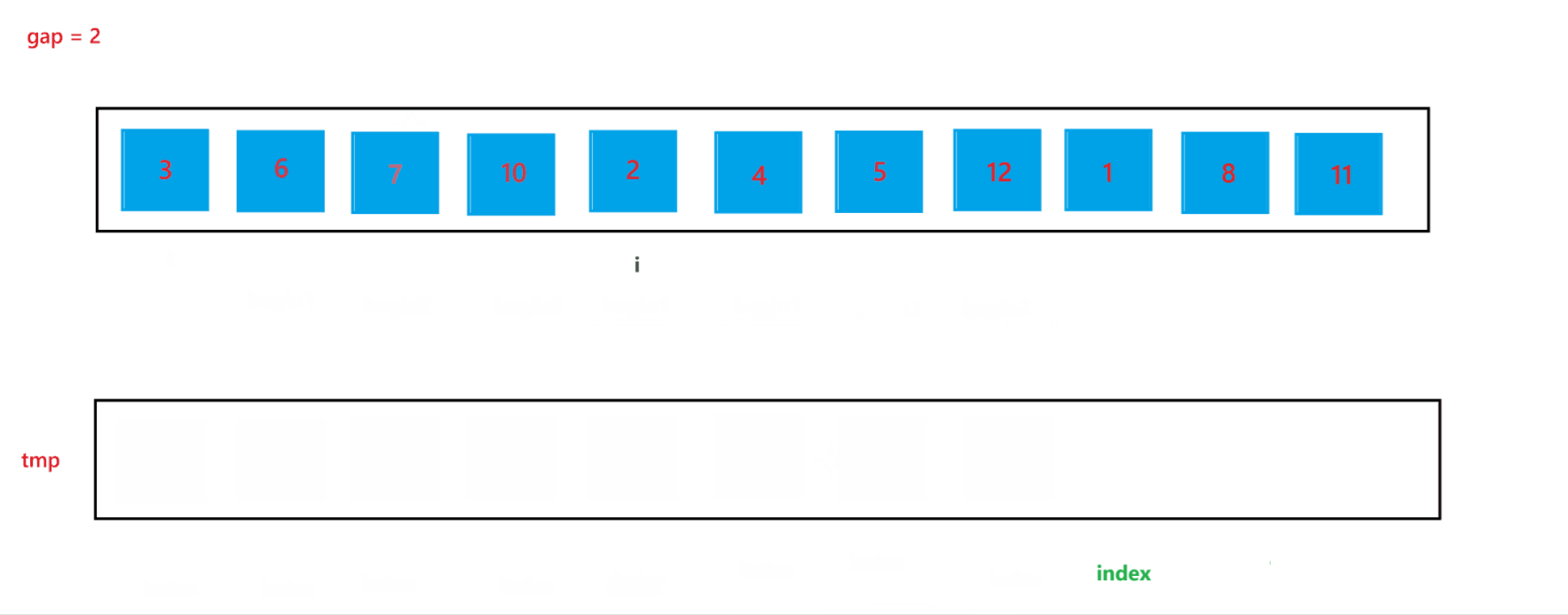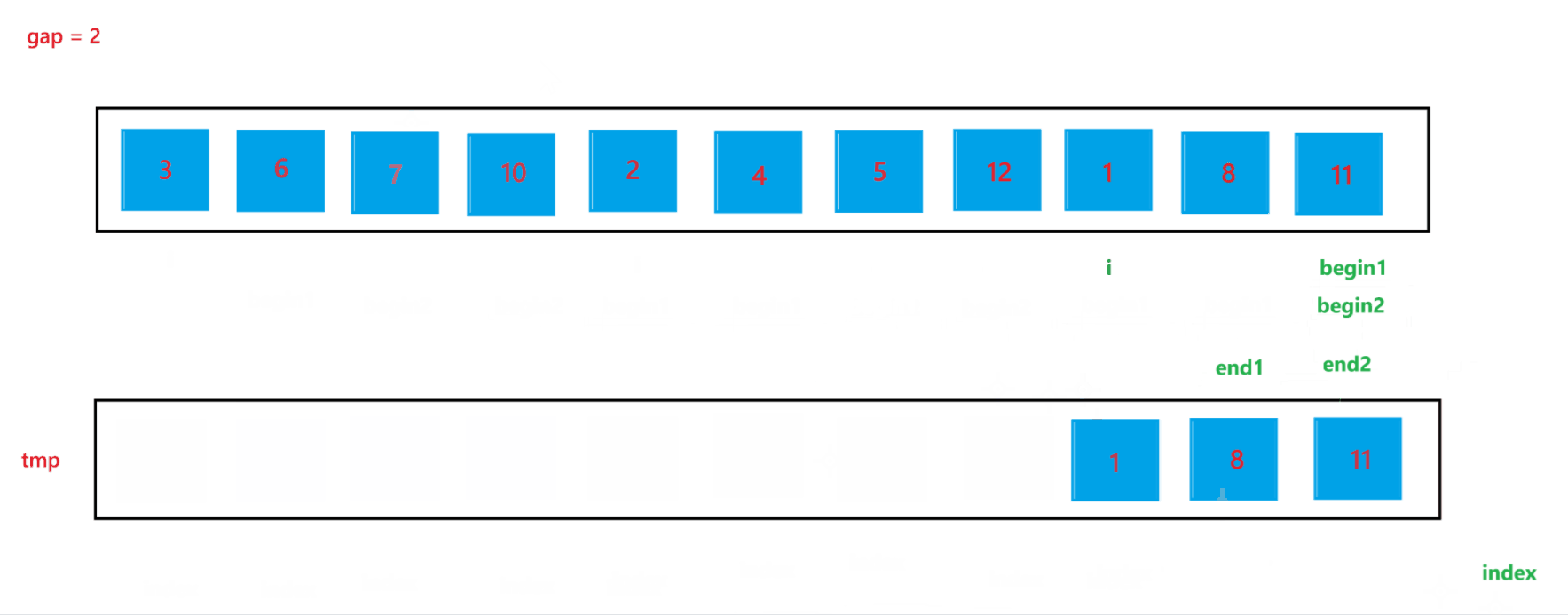
通过上述合并过程,可以看到当 end2 出现越界行为时,我们让其回到了最后一个位置,也就是 end2 = n - 1,此时就可以避免越界行为的发生。
接下来 gap 会继续 gap *= 2,变为4,之后会再变为 8,最后变为 16 的时候由于大于 n,会退出循环,排序就完成了,如果你有兴趣可以自己画一下图模拟一下过程,在这里就不再画图。
2) 代码
void MergeSortNorR(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail!\n");
exit(1);
}
//每组元素的个数
int gap = 1;
while (gap < n)
{
//遍历每两组,进行两组之间的合并
// i 每次指向要合并两组的第一组的第一个元素
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
int index = begin1;
//为了防止要合并第二个数组越界,需要特殊处理一下
//begin2 如果越界,代表第一组没有要合并的第二组了,不用合并了,直接跳出循环
if (begin2 >= n)
{
break;
}
//如果要合并的第二组元素不满gap个,那就有多少合并多少
if (end2 >= n)
{
end2 = n - 1;
}
//合并两个有序数组
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//把tmp中的数据放回原数组
memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
//最后不要忘记释放tmp数组
free(tmp);
tmp = NULL;
}测试用例:
#include<stdio.h>
#include<stdlib.h>
void MergeSortNorR_Test()
{
//奇数个元素的情况
//int arr[] = { 2, 1, 10, 4, 7, 3, 8, 5, 11 };
//偶数个元素的情况
int arr[] = { 2, 1, 10, 4, 7, 3, 8, 5 };
int n = sizeof(arr) / sizeof(arr[0]);
MergeSortNorR(arr, n);
for (int i = 0; i < n; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
MergeSortNorR_Test();
return 0;
}3 文件的归并排序
1) 外排序
不同于内排序,外排序是进行文件与磁盘内数据的排序,也就是不是直接对存储在内存中的数据进行排序,而是先将外存中的数据先调入内存,排完序之后再将数据放回文件或者磁盘中,就是外排序。
那么什么时候会用到外排序呢?一般都是数据量很多时,比如一个文件里面有 10G 的数据,无法全部调入内存,还想要对文件内的数据进行排序,此时就需要进行外排序。
2) 文件的归并排序
(1) 算法思想
如果想要排序的数据量较大时,我们一般都会先把数据保存在文件中,然后通过 C 语言中文件的相关操作,将文件中的数据排序好后,再放入文件之中,而在七大排序算法中,不需要内存的随机访问而又效率比较快的排序算法就是归并排序了(堆排序、快速排序、希尔排序都需要对内存中的数据进行随机访问),所以归并排序算法既可以用于实现内排序,也可以实现外排序,以下是对文件进行归并排序的算法过程:
a. 先在要进行排序的文件 data.txt 中取出 n 个数据,将这 n 个数据排好序后,放到 file1.txt 里面;再取出 n 个数据,排好序之后,放到 file2.txt 文件里面。
b. 然后对 file1.txt 和 file2.txt 中的数据进行归并(就是前面归并排序中合并两个有序子数组的过程),将归并后的数据放到 mfile.txt 里面。
c. 此时,file1.txt 与 file2.txt 已经没用了,删除 file1,txt 与 file2.txt 文件,将 mfile.txt 文件重命名为 file1.txt 文件。
d. 然后再取出 n 个数据放到 file2.txt 里面,再将 file1.txt(之前的 mfile.txt 文件)与 file2.txt 文件归并,将归并后的数据放到新的 mfile.txt 文件里面;如此循环,直到 data.txt 文件中没有数据为止。最终,排好序的数据会存储在 file1.txt 文件里面。
上述算法过程如下图所示:
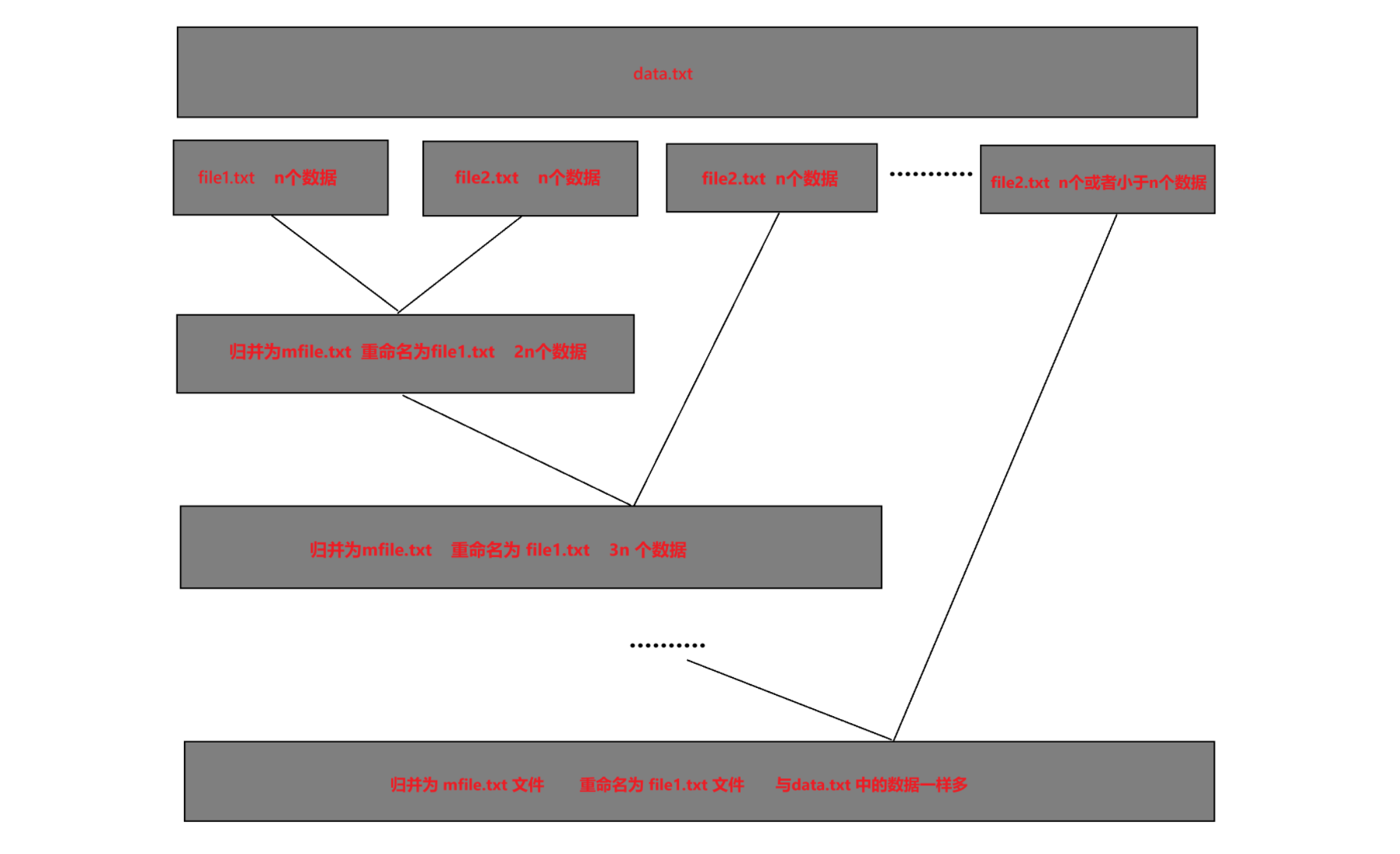
在上述算法思想的实现过程中,有三个函数需要我们了解一下,第一个就是删除文件的函数,第二个就是对文件名重命名的函数,还有一个就是对数据进行排序的函数,接下来我们来一次了解一下。
a. 删除文件的函数:

删除文件的函数的函数名字叫做 remove 函数,与 printf 和 scanf 函数相同,其都被包含在 stdio.h 头文件下,传入的参数仅有一个,就是要删除文件的文件名字符指针即可。所以删除 file1.txt 文件与 file2.txt 文件,我们可以直接 remove("file1.txt") 与 remove("file2.txt")。
b. 重命名的函数:

对文件进行重命名的函数叫做 rename 函数,传入的参数也很简单,第一个参数为要修改的文件的文件名的字符指针,也就是 oldname,第二个参数为修改后的文件名的字符指针,也就是 newname。所以将 mfile 重命名为 file1.txt 可以写为 rename("mfile.txt", "file1.txt")。
c. 对数据进行排序的函数:这里可以使用我们之前学习过的七大排序算法,比如:快速排序、堆排序、希尔排序都可以,当然这里也可以直接使用 qsort 函数:

可以看到 qsort 函数是需要四个参数的,第一个是需要进行排序的首元素的指针,第二个参数是进行排序的元素的个数,第三个参数是需要进行排序的元素的大小(单位为字节),第四个参数是一个函数指针,其指向的函数的返回值为 int, 两个参数类型为 const void*。对于第四个参数 compare 我们具体讲解一下:
从下面的表格我们可以看出其对返回值是有要求的,如果第一个参数想排在第二个参数之前,那就返回小于 0 的数字;如果相等返回 0;否则返回大于 0 的数字,由于我们这里排的都是整形,且升序排序,所以我们可以这样设计 compare 函数:
int compare(const void* a, const void* b)
{
return (*(int*)a - *(int*)b);
}注意,一定要对 a 和 b 进行强转,因为 void* 类型的指针无法进行解引用的。
(2) 代码
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void CreateData()
{
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen fail!\n");
exit(1);
}
srand(time(0));
const int n = 1000000;
for (int i = 0; i < n; i++)
{
fprintf(fin, "%d\n", rand() + i);
}
fclose(fin);
}
int Compare(const void* a, const void* b)
{
return (*(int*)a - *(int*)b);
}
//返回读取到的数据个数
int SortNValeToFile(FILE* fout, int n, const char* file)
{
int x = 0;
int* a = (int*)malloc(sizeof(int) * n);
if (a == NULL)
{
perror("malloc error");
return 0;
}
// 想读取n个数据,如果遇到文件结束,应该读到j个
int j = 0;
for (int i = 0; i < n; i++)
{
if (fscanf(fout, "%d", &x) == EOF)
break;
a[j++] = x;
}
if (j == 0)
{
free(a);
return 0;
}
// 排序
qsort(a, j, sizeof(int), Compare);
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
free(a);
perror("fopen error");
return 0;
}
// 写回file1文件
for (int i = 0; i < j; i++)
{
fprintf(fin, "%d\n", a[i]);
}
free(a);
fclose(fin);
return j;
}
void MergeFile(const char* file1, const char* file2, const char* mfile)
{
FILE* fout1 = fopen(file1, "r");
if (fout1 == NULL)
{
perror("fopen1 fail!\n");
return;
}
FILE* fout2 = fopen(file2, "r");
if (fout2 == NULL)
{
perror("fopen2 fail!\n");
return;
}
FILE* fin = fopen(mfile, "w");
if (fin == NULL)
{
perror("fin fail!\n");
return;
}
//对文件进行归并排序
int x1 = 0;
int x2 = 0;
int ret1 = fscanf(fout1, "%d", &x1);
int ret2 = fscanf(fout2, "%d", &x2);
while (ret1 != EOF && ret2 != EOF)
{
//如果 file1 的数据小于 file2 的数据,就将 file1 的数放到 mfile 里面
if (x1 < x2)
{
fprintf(fin, "%d\n", x1);
ret1 = fscanf(fout1, "%d", &x1);
}
else
{
fprintf(fin, "%d\n", x2);
ret2 = fscanf(fout2, "%d", &x2);
}
}
while (ret1 != EOF)
{
fprintf(fin, "%d\n", x1);
ret1 = fscanf(fout1, "%d", &x1);
}
while (ret2 != EOF)
{
fprintf(fin, "%d\n", x2);
ret2 = fscanf(fout2, "%d", &x2);
}
fclose(fout1);
fclose(fout2);
fclose(fin);
}
int main()
{
CreateData();
//创建三个文件
const char* file1 = "file1.txt";
const char* file2 = "file2.txt";
const char* mfile = "mfile.txt";
//从data.txt中取出n个数据放到file1与file2中
FILE* fout = fopen("data.txt", "r");
if (fout == NULL)
{
perror("fopen fail!\n");
exit(1);
}
int N = 100000;
SortNValeToFile(fout, N, file1);
SortNValeToFile(fout, N, file2);
while (1)
{
//将两个文件归并到 mfile 文件
MergeFile(file1, file2, mfile);
//删除file1 与 file2 文件
remove(file1);
remove(file2);
//将mfile 重命名为 file1
rename(mfile, file1);
//再从data.txt中取出n个数据放到file2 里面
//如果取不到数据说明归并结束
if (SortNValeToFile(fout, N, file2) == 0)
break;
}
return 0;
}