目录
一、斐波那契数列(兔子问题)
学习递归函数,分析递归流程。
斐波那契是中世纪一个有名的数学家,他在计算之书中提出了一个有趣的:
兔子问题:
# 若一对成年兔子,每个月生下一对小兔子,恰好一雌一雄。
# 在年初时,只有一对小兔子。
# 第1个月结束时,他们成长为成年兔子。
# 第2个月结束时,这对成年兔子,则生下一对小兔子。
# 这种成长与繁殖过程一直持续下去,并假设生下的小兔子不会死,那么一年之后将会有多少只兔子?
# 推算第5个月兔子总数。#第1个月:1对兔子。
#第2个月:小兔子长大,仍然1对兔子。
#第3个月:这对兔子生了1对小兔子,所以有2对兔子。
#第4个月:老兔子又生了1对兔子,而上个月新出生的兔子还未成熟,所以有3对兔子。
#第5个月:这是已经有2对兔子可以繁殖,于是生了2对兔子。所以有5对兔子。#第n个月的兔子总数=第n-1个月的兔子总数+第n-2个月的兔子总数
#斐波那契数列(黄金分割):1,1,2,3,5,8,13,21,34,55...
#取出最后得到的两个数,取出21和34,21÷34约等于0.618,是黄金分割比例。
二、迭代法(用while循环推下一项 )
#用while循环推倒斐波那契数列下一项:
#斐波那切数列:假如这个函数可以生成斐波那切数列第n项:
#例如:0,1,1,2,3,5,8,13,21,34,55...
#fibo(0)=0,fibo(1)=1,fibo(2)=1;
#当fibo(n)时,返回就是斐波那切数列对应的第n项。
def fibo(n):
#斐波那切数列的前两项是:0,1
fibo_list=[0,1]
##**变量i
i=2
#让列表包括斐波那切的所有数字,直到第n项,写while循环。
while i<=n:
##每次推导出数列的下一个数值num(第i项第值num,规律)
num=fibo_list[i-1]+fibo_list[i-2]
# append方法添加到列表的最后
fibo_list.append(num)
#添加到最后一项循环结束
##加1操作
i+=1
#返回斐波那契额数列第n项
return fibo_list[n]
#因为数列第0,1项已知,所以添加第2项到数列,变量i
#1.打印第5项
print(fibo(5))
#2.打印0-10项
# for j in range(10):
# print(fibo(j)) #打印前10项#递归函数:def funA():
#在函数内部可以调用其他函数,如果一个函数直接或者间接调用函数本身,是递归函数
三、递归函数
(函数的定义中调用函数自身的一种函数定义方式)
# f(0)=0
# f(1)=1
# f(2)=1=0+1=f(1)+f(0)
# f(3)=2=1+1=f(2)+f(1)
#f(n)=f(n-1)+f(n-2)
def fibo(n):
if n==0:
return 0
elif n==1:
return 1
# if n<2:
# return n
else:
return fibo(n-1)+fibo(n-2) #函数内调用了这个,所以递归
for j in range(10):
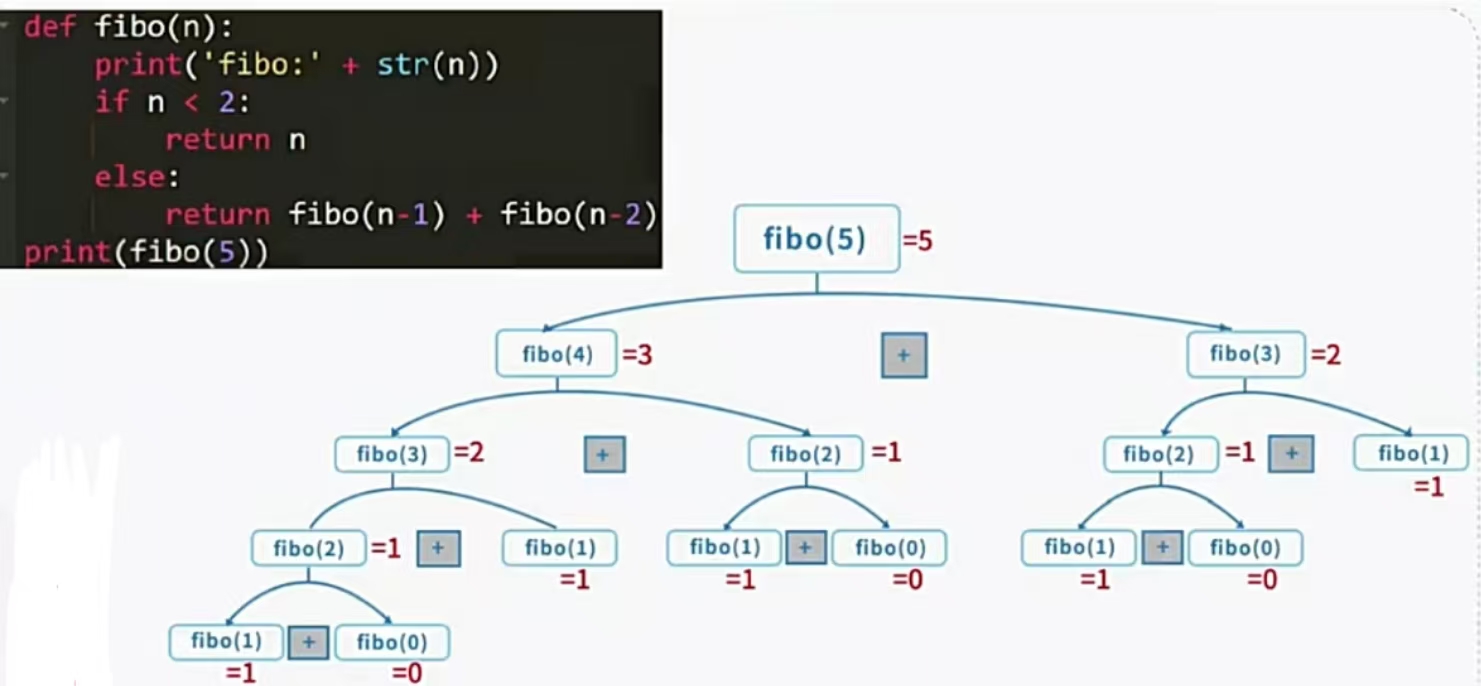
print(fibo(j))四、递归函数的底层逻辑推理
(二叉树推倒最左下节点回退法)
#定义简单,逻辑清晰
#过程中发生了什么,树形图
def fibo(n):
print('fibo:'+str(n))
if n<2:
return n
else:
return fibo(n-1) + fibo(n-2)
print(fibo(3))
#print(fibo(6))