目录
一、图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E)。
1.1 图的基本组成
顶点(Vertex)
- 图的基本元素,代表具体的对象(如城市、网络节点等),通常用 V 表示顶点集合。
边(Edge)
- 顶点之间的连接关系,代表对象间的关系(如道路、通信链路等),通常用 E 表示边集合。
- 有向边:带有方向的边(用箭头表示),构成有向图。
- 无向边:没有方向的边,构成无向图。
1.2 图的分类
按边的方向性分类
- 无向图:所有边均为无向边,边记为 (u, v),且 (u, v)= (v, u) 。
- 有向图:至少存在一条有向边,边记为 <u, v>,表示从 u 到 v 的方向。
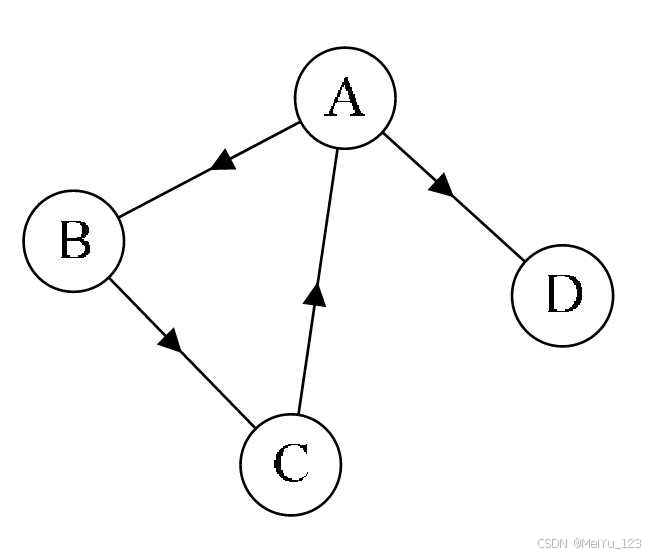
有向图

无向图
按边是否有权值分类
- 无权图:边仅表示连接关系,无权重(如是否可达)。
- 加权图:每条边带有数值权重(如距离、成本等)。

加权图
按是否有重复边或自环分类
- 简单图:无重复边、无自环(顶点到自身的边)。
- 多重图:允许重复边(平行边)或自环。
- 完全图:任意两个顶点之间都有一条边(无向完全图有 (n(n-1)2) 条边,有向完全图有 (n(n-1)) 条边,n 为顶点数)。
1.3 顶点的度数
无向图中的度数(Degree)
- 顶点 v 的度数是其连接的边数。
- 所有顶点度数之和等于边数的 2 倍(每条边被两个顶点各计数一次)。
- 有向图中的度数
- 入度:指向顶点 v 的边数。
- 出度:顶点 v 发出的边数。
- 顶点度数 = 入度 + 出度。
1.4 路径与回路
- 路径
- 顶点序列 (V1, V2, ......, Vk),其中相邻顶点由边连接。
- 简单路径:路径中所有顶点互不重复(除起点和终点可能相同)。
回路
- 起点和终点相同的路径(长度 ≥ 1)。
- 简单回路:除起点和终点外,其余顶点互不重复的回路。
连通性
- 无向图:若任意两顶点存在路径,则图是连通图;否则分为多个连通分量。
- 有向图:若任意两顶点 (u -> v) 和 (v -> u) 均有路径,则为强连通图;否则分为强连通分量。
1.5 子图与特殊图
子图
- 顶点集和边集均为原图子集的图。
二分图
- 顶点可分为两个不相交的集合,所有边均连接两个集合中的顶点(无同一集合内的边)。
树
- 无向图中,连通且无回路的图(顶点数 n,边数 (n-1))。
- 有向树:有向图中,仅有一个根节点(入度为 0),其余顶点入度为 1,且从根到所有顶点有唯一路径。
二. 图的存储结构
2.1 邻接矩阵
核心思想:
用一个二维矩阵 A 表示顶点之间的连接关系,矩阵大小为 (n * n)(n 为顶点数)
- 无权图:(A[i][j] = 1) 表示存在边 (i -> j)(有向图)或 ((i,j))(无向图),否则为 0。
- 加权图:(A[i][j] = w) 表示边的权重为 w,无边则设为无穷大。

优点:
- 访问边的时间复杂度为(O(1))(直接查矩阵)。
- 适合表示稠密图(边数接近 (n^2))。
缺点:
- 空间复杂度为 (O(n^2)),存储稀疏图(边数少)时浪费空间。
- 遍历一个顶点的所有邻接点需要扫描整行,效率低(O(n))。
2.2 邻接表
每个顶点对应一个列表,存储其相邻顶点(有向图存储出边,无向图存储所有邻接顶点)。
- 无权图:链表中存储相邻顶点的编号。
- 加权图:链表中存储二元组 ((邻接顶点, 权重))。

优点:
- 空间复杂度为 (O(n + e))(e 为边数),适合表示稀疏图。
- 遍历一个顶点的所有邻接点效率高(只需遍历其链表)。
缺点:
- 检查某条边是否存在需要遍历链表。
- 无向图中每条边会被存储两次(在两个顶点的链表中)。
三、深度优先遍历
3.1 原理
深度优先搜索是一种图遍历算法,它沿着一条路径尽可能深入,直到无法继续为止,然后回溯到上一个节点,尝试其他路径。DFS 使用递归或栈实现,适合用于遍历所有可能的路径。
3.2 实现步骤
- 从起点开始:
- 标记当前节点为已访问。
- 输出或处理当前节点。
- 递归访问邻接节点:
- 遍历当前节点的所有邻接节点。
- 如果某个邻接节点未访问,递归调用 DFS。
- 回溯:
- 在递归返回时,回到上一个节点,继续探索其他未访问的邻接节点。
3.3 代码实现
#include <iostream>
#include <vector>
void dfs(const std::vector<std::vector<int>>& graph, int node, std::vector<bool>& visited) {
visited[node] = true;
std::cout << node << " "; // 访问节点
for (int i = 0; i < graph.size(); ++i)
{
if (graph[node][i] == 1 && !visited[i])
{
dfs(graph, i, visited);
}
}
}
int main()
{
// 示例图(邻接矩阵表示)
std::vector<std::vector<int>> graph =
{
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0}
};
std::vector<bool> visited(graph.size(), false);
std::cout << "DFS: ";
dfs(graph, 0, visited); // 从节点 0 开始
std::cout << std::endl;
return 0;
}四、广度优先遍历
4.1 原理
广度优先搜索是一种逐层遍历图的算法。它从起点开始,先访问所有直接邻接的节点,然后再访问这些节点的邻接节点。BFS 的特点是“逐层扩展”。
4.2 实现步骤
- 初始化队列:
- 将起点加入队列,并标记为已访问。
- 逐层遍历:
- 从队列中取出一个节点。
- 输出或处理该节点。
- 遍历当前节点的所有邻接节点:
- 如果某个邻接节点未访问,将其加入队列,并标记为已访问。
- 重复:
- 继续从队列中取出节点,直到队列为空。
4.3 代码实现
#include <iostream>
#include <queue>
#include <vector>
void bfs(const std::vector<std::vector<int>>& graph, int start)
{
int n = graph.size();
std::vector<bool> visited(n, false);
std::queue<int> q;
visited[start] = true;
q.push(start);
while (!q.empty())
{
int node = q.front();
q.pop();
std::cout << node << " "; // 访问节点
for (int i = 0; i < n; ++i)
{
if (graph[node][i] == 1 && !visited[i])
{
visited[i] = true;
q.push(i);
}
}
}
}
int main()
{
// 示例图(邻接矩阵表示)
std::vector<std::vector<int>> graph = {
{0, 1, 1, 0, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0}
};
std::cout << "BFS: ";
bfs(graph, 0); // 从节点 0 开始
std::cout << std::endl;
return 0;
}结语
最近笔试老是最后一题出个图相关的,写这篇文章是为了复习图的相关知识点与遍历方法,临阵磨枪,希望在接下来的笔试中能应对这种题目。