[高阶数据结构]二叉树经典面试题

发布于：2025-05-13 ⋅ 阅读:(14) ⋅ 点赞:(0)

二叉树经典面试题：：

目录

二叉树经典面试题：：

1.根据二叉树创建字符串

2.二叉树的层序遍历

3.二叉树的层序遍历II

4.二叉树的最近公共祖先

5.二叉树与双向链表

6.从前序与中序序列构造二叉树

7.从中序与后序序列构造二叉树

8.非递归实现二叉树的前序遍历

9.非递归实现二叉树的中序遍历

10.非递归实现二叉树的后序遍历

11.前K个高频单词

12.在长度2N的数组中找出重复N次的元素

13.两个数组的交集I

14.两个数组的交集II

15.两句话中的不常见单词

1.根据二叉树创建字符串

struct TreeNode 
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right)             {}
};
 
class Solution 
{
public:
	string tree2str(TreeNode* root) 
	{
		if (root == nullptr)
		{
			return string();
		}
		string str;
		str += to_string(root->val);
		if (root->left != nullptr)
		{
			str += '(';
			str += tree2str(root->left);
			str += ')';
		}
		else if(root->left == nullptr && root->right != nullptr)
		{
			str += "()";
		}
		
		if (root->right != nullptr)
		{
			str += '(';
			str += tree2str(root->right);
			str += ')';
		}
		//右边为空则不处理
		return str;
	}
};

2.二叉树的层序遍历

struct TreeNode 
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution 
{
public:
	vector<vector<int>> levelOrder(TreeNode* root) 
	{
		queue<TreeNode*> q;
		vector<vector<int>> vv;
		int levelSize = 0;
		if (root != nullptr)
		{
			q.push(root);
			levelSize = 1;
		}
		while (!q.empty())
		{
			//一层一层出
			vector<int> levelv;
			while (levelSize--)
			{
				TreeNode* front = q.front();
				q.pop();
				levelv.push_back(front->val);
				if (front->left != nullptr)
				{
					q.push(front->left);
				}
				if (front->right != nullptr)
				{
					q.push(front->right);
				}
			}
			vv.push_back(levelv);
			//当前一层出完 下一层全部进入队列 那么size就是下一层的数据个数
			levelSize = q.size();
			
		}
		return vv;
	}
};

3.二叉树的层序遍历II

struct TreeNode
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
	vector<vector<int>> levelOrderBottom(TreeNode* root)
	{
		queue<TreeNode*> q;
		vector<vector<int>> vv;
		int levelSize = 0;
		if (root != nullptr)
		{
			q.push(root);
			levelSize = 1;
		}
		while (!q.empty())
		{
			vector<int> levelv;
			while (levelSize--)
			{
				TreeNode* front = q.front();
				q.pop();
				levelv.push_back(front->val);
				if (front->left != nullptr)
				{
					q.push(front->left);
				}
				if (front->right != nullptr)
				{
					q.push(front->right);
				}
			}
			vv.push_back(levelv);
			levelSize = q.size();

		}
		reverse(vv.begin(), vv.end());
		return vv;
	}
};

4.二叉树的最近公共祖先

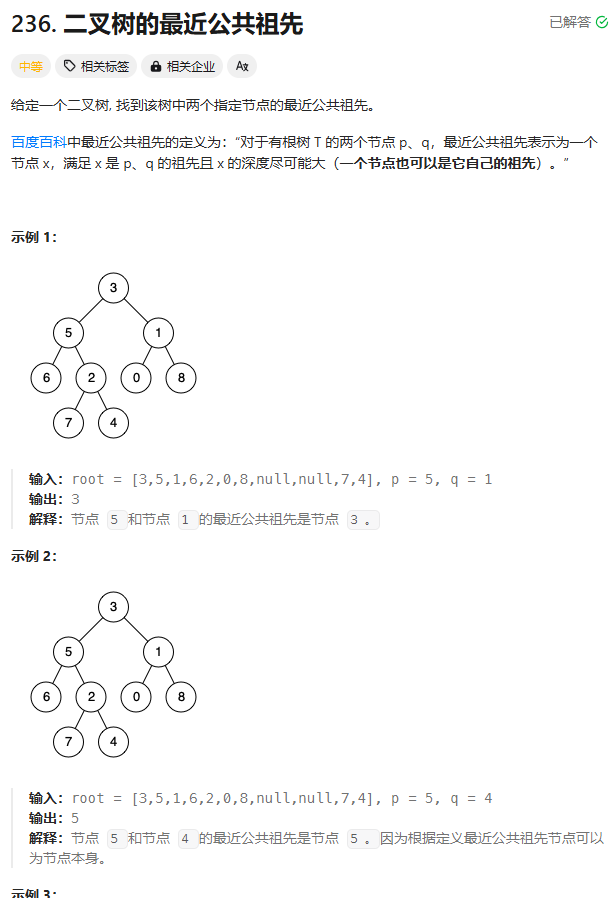
 struct TreeNode
 {
       int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 };

class Solution
{
public:
	bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
	{
		if (root == nullptr)
		{
			return false;
		}
		path.push(root);
		if (root == x)
		{
			return true;
		}
		if (GetPath(root->left, x, path))
		{
			return true;
		}
		if (GetPath(root->right, x, path))
		{
			return true;
		}
		path.pop();
		return false;
	}


	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
	{
		stack<TreeNode*> pPath;
		stack<TreeNode*> qPath;
		GetPath(root, p, pPath);
		GetPath(root, q, qPath);

		//找路径相遇点
		while (pPath.size() != qPath.size())
		{
			if (pPath.size() > qPath.size())
			{
				pPath.pop();
			}
			else
			{
				qPath.pop();
			}
		}

		while (pPath.top() != qPath.top())
		{
			pPath.pop();
			qPath.pop();
		}
		return pPath.top();
	}

};

5.二叉树与双向链表

struct TreeNode
{
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) 
    {}
};
class Solution 
{
public:
	void InOrderConvert(TreeNode* cur, TreeNode*& prev)
	{
		if (cur == nullptr)
		{
			return;
		}
		InOrderConvert(cur->left, prev);
		cur->left = prev;
		if (prev != nullptr)
		{
			prev->right = cur;
		}
		prev = cur;
		InOrderConvert(cur->right, prev);
	}
	TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		TreeNode* prev = nullptr;
		InOrderConvert(pRootOfTree, prev);
		TreeNode* head = pRootOfTree;
		while (head != nullptr && head->left != nullptr)
		{
			head = head->left;
		}
		return head;
	}
};

6.从前序与中序序列构造二叉树

struct TreeNode 
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend) 
    {
        //中序区间不存在则是空树
        if (inbegin > inend)
        {
            return nullptr;
        }
        //划分左右区间
        int rooti = inbegin;
        while (rooti <= inend)
        {
            if (inorder[rooti] ==preorder[prei])
            {
                break;
            }
            ++rooti;
        }
        TreeNode* root = new TreeNode(preorder[prei]);
        ++prei;
        //[inbegin,rooti-1] rooti [rooti+1,inend]
        root->left = _buildTree(preorder, inorder, prei, inbegin, rooti - 1);
        root->right = _buildTree(preorder, inorder, prei, rooti + 1, inend);
        return root;

    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
    {
        int pi = 0;
        return _buildTree(preorder, inorder, pi, 0, inorder.size() - 1);
    }
};

7.从中序与后序序列构造二叉树

struct TreeNode 
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution 
{
public:
	TreeNode* _buildTree(vector<int>& inorder, int inbegin, int inend, vector<int>& postorder, int& pi)
	{
		if (inbegin > inend)
		{
			return nullptr;
		}
		TreeNode* root = new TreeNode(postorder[pi]);
		pi--;
		//将该子树的中序遍历序列划分为其左子树和右子树的中序遍历序列
		int rooti = inbegin;
		while (inorder[rooti] != root->val)
		{
			rooti++;
		}
		root->right = _buildTree(inorder, rooti + 1, inend, postorder, pi);
		root->left = _buildTree(inorder, inbegin, rooti - 1, postorder, pi);
		return root;
	}
	TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) 
	{
		int i = postorder.size() - 1; 
		return _buildTree(inorder, 0, inorder.size() - 1, postorder, i);
	}
};

8.非递归实现二叉树的前序遍历

struct TreeNode 
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };
class Solution
{
public:
    vector<int> preorderTraversal(TreeNode* root) 
    {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (!st.empty() || cur != nullptr)
        {
            //准备开始访问一棵树
            //访问左路结点
            //左路结点的右子树
            while (cur != nullptr)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }
            //左路结点右子树
            TreeNode* top = st.top();
            st.pop();
            //循环子问题访问右子树
            cur = top->right;

        }
        return v;
    }
};

9.非递归实现二叉树的中序遍历

 struct TreeNode
 {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };
class Solution 
{
public:
    vector<int> inorderTraversal(TreeNode* root) 
    {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur || !st.empty())
        {
            while (cur)
            {
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            st.pop();

            v.push_back(top->val);
            
            //访问右子树
            cur = top->right;
        }
        return v;
    }
};

10.非递归实现二叉树的后序遍历

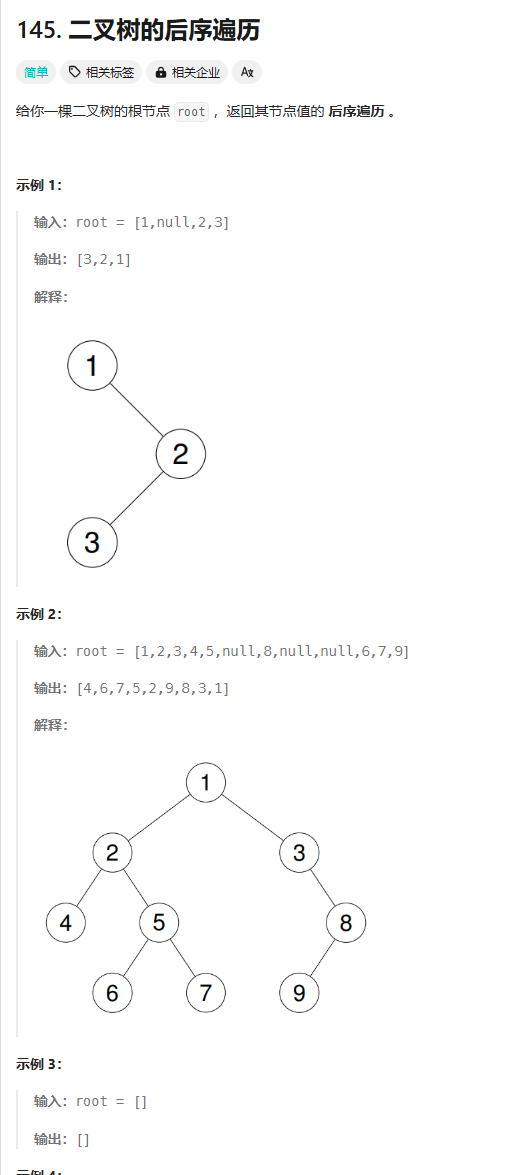
struct TreeNode
{
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
    vector<int> postorderTraversal(TreeNode* root)
    {
        vector<int> v;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* prev = nullptr;
        while (cur || !st.empty())
        {
            while (cur)
            {
                st.push(cur);
                cur = cur->left;
            }

            TreeNode* top = st.top();
            //1.top的右子树为空或者右子树已经访问过了(上一个访问的结点是右子树的根)
            //那么说明右子树不用访问或者访问过了，可以访问根top
            //2.右子树不为空且没有访问，则迭代子问题访问
            if (top->right == nullptr || top->right == prev)
            {
                st.pop();
                v.push_back(top->val);
                prev = top;
            }
            else
            {
                cur = top->right;
            }
        }
        return v;
    }
};

11.前K个高频单词

class Solution 
{
public:
    struct Compare
    {
        bool operator()(const pair<int, string>& l, const pair<int, string>& r)
        {
            return l.first > r.first;
        }
    };
public:
    vector<string> topKFrequent(vector<string>& words, int k)
    {
        map<string, int> countMap;
        for (auto& str : words)
        {
            countMap[str]++;
        }
        vector<pair<int, string>> v;
        for (auto& kv : countMap)
        {
            v.push_back(make_pair(kv.second, kv.first));
            cout << kv.first << ":" << kv.second << endl;
        }
        stable_sort(v.begin(), v.end(), Compare());

        vector<string> ret;
        for (int i = 0; i < k; i++)
        {
            ret.push_back(v[i].second);
        }
        return ret;
    }
};

12.在长度2N的数组中找出重复N次的元素

class Solution 
{
public:
	int repeatedNTimes(vector<int>& A) 
	{
		size_t N = A.size() / 2;
		// 用unordered_map统计每个元素出现的次数
		unordered_map<int, int> m;
		for (auto e : A)
		{
			m[e]++;
		}

		// 找出出现次数为N的元素
		for (auto& e : m)
		{
			if (e.second == N)
			{
				return e.first;
			}
		}
		return -1;
	}
};

13.两个数组的交集I

class Solution
{
public:
	vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {

		// 用unordered_set对nums1中的元素去重
		unordered_set<int> s1;
		for (auto e : nums1)
		{
			s1.insert(e);
		}

		// 用unordered_set对nums2中的元素去重
		unordered_set<int> s2;
		for (auto e : nums2)
		{
			s2.insert(e);
		}
		// 遍历s1，如果s1中某个元素在s2中出现过，即为交集
		vector<int> vRet;
		for (auto e : s1)
		{
			if (s2.find(e) != s2.end())
			{
				vRet.push_back(e);
			}
		}
		return vRet;
	}
};

14.两个数组的交集II

//哈希表
class Solution 
{
public:
	vector<int> intersect(vector<int>& nums1, vector<int>& nums2) 
	{
		//为了降低空间复杂度，应该先将元素个数较少的数组放入哈希表
		if (nums1.size() > nums2.size())
		{
			return intersect(nums2, nums1);
		}
		//1、将nums1中的每个数字以及对应出现的次数放入哈希表中
		unordered_map<int, int> um;
		for (auto e : nums1)
		{
			um[e]++;
		}
		//2、遍历nums2，找出nums1和nums2的交集
		vector<int> vRet;
		for (auto e : nums2)
		{
			if (um.count(e)) //该元素在哈希表中
			{
				vRet.push_back(e); //该元素属于交集
				um[e]--; //减少该元素在哈希表中出现的次数
				if (um[e] == 0) //该元素的次数已经变为0了
				{
					um.erase(e); //将该元素从哈希表中删除
				}
			}
		}
		return vRet;
	}
};

15.两句话中的不常见单词

class Solution 
{
public:
	vector<string> uncommonFromSentences(string s1, string s2) 
	{
		unordered_map<string, int> um;
		//1、将两个字符串拼接起来，中间加一个" "字符串
		string str = s1 + " " + s2;

		//2、将拼接后字符串当中的单词放入哈希表
		size_t start = 0; //字头
		size_t pos = str.find(' '); //字尾
		while (pos != string::npos) //直到找到字符串结尾
		{
			string word = str.substr(start, pos - start); //将单词提取出来
			um[word]++; //将单词放入哈希表
			start = pos + 1; //更新字头
			pos = str.find(' ', start); //更新字尾
		}
		//将最后一个单词放入哈希表
		string word = str.substr(start);
		um[word]++;

		//3、找出哈希表中只出现过一次的单词，即不常见单词
		vector<string> vRet;
		for (auto e : um)
		{
			if (e.second == 1) //只出现过一次的单词
			{
				vRet.push_back(e.first);
			}
		}
		return vRet;
	}
};

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布