PyTorch循环神经网络（Pytotch）

循环神经网络（RNN）

• 循环神经网络（RecurrentNeuralNetwork，RNN）又称递归神经网络，它是常规前馈神经网络（FeedforwardNeuralNetwork，FNN）的扩展，本节介绍几种常见的循环神经网络。

简单的循环神经网络

• 循环神经网络（RNN）会遍历所有序列的元素，每个当前层的输出都与前面层的输出有关，会将前面层的状态信息保留下来。理论上，RNN应该可以处理任意长度的序列数据，但为了降低一定的复杂度，实践中通常只会选取与前面的几个状态有关的信息。
• 简单的循环神经网络如图：
  
• x是输入，y是输出，中间由一个箭头表示数据循环更新的是隐藏层，主要由中间部分实现时间记忆功能。
• 神经网络输入x并产生输出y，最后将输出的结果反馈回去。假设在一个时间t内，神经网络的输入除来自输入层的$x(t)$外，还有上一时刻的输出$y(t-1)$，两者共同输入产生当前层的输出$y(t)$。
• 将这个神经网络按照时间序列形式展开：
  
• 每个神经元的输出都是根据当前的输入$x(t)$和上一时刻的$y(t-1)$共同决定。它们对应的权重分别是$W_x$和$W_y$，单个神经元的输出计算如下：
  $${\mathbf{y}}_t=\mathcal{O}({\mathbf{x}}_t^{\mathrm{T}}\cdot {\mathbf{W}}_x+{\mathbf{y}}_{t-1}^{\mathrm{T}}\cdot {\mathbf{W}}_y+b)$$
• 将隐藏层的层级展开，结果如下图：
  
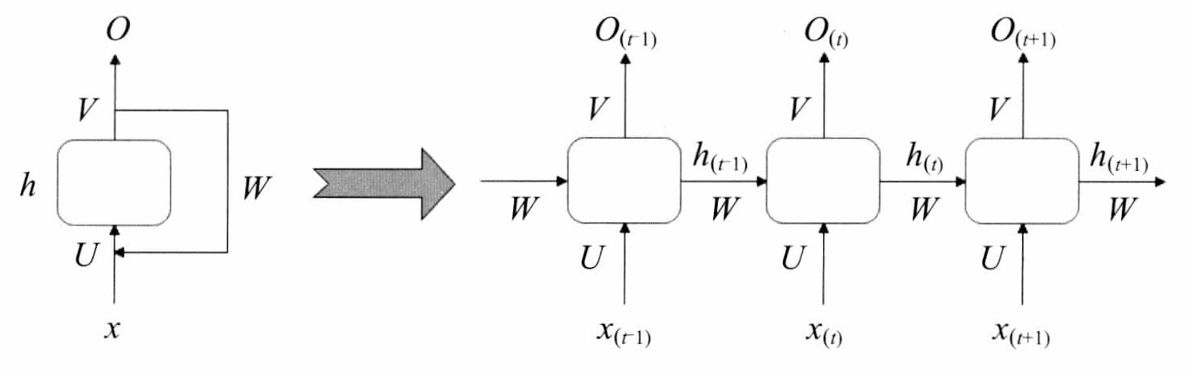
• RNN单元在时间$t$的状态记作$h_t$，$U$表示此刻输入的权重，$W$表示前一次输出的权重，$V$表示此刻输出的权重。
• 在$t=1$时刻，一般$h_0$表示初始状态为0，随机初始化$U、W、V$，公式如下：
  $$\begin{array}{l}{h}_1=f(U{x}_1+W{h}_0+b_h)\\ O_1=g(V{h}_1+b_o)\end{array}$$
• f 和 g 均为激活函数（光滑的曲线函数），$f$可以是Sigmoid、ReLU、Tanh等激活函数，$g$通常是Softmax损失函数。$b_h$是隐藏层的偏置项，$b_0$是输出层的偏置项。
• 前向传播算法，按照时间$t$向前推进，而此时隐藏状态$h_1$是参与下一个时间的预测过程。
  $$\begin{array}{l}{h}_2=f(U{x}_2+W{h}_1+b_h)\\ O_2=g(V{h}_2+b_o)\end{array}$$
• 以此类推，最终可得到输出公式为：
  $$\begin{array}{l}{h}_t=f(U{x}_t+W{h}_{t-1}+b_h)\\ O_t=g(V{h}_t+b_o)\end{array}$$
• 权重共享机制通过统一网络参数（W、U、V及偏置项）实现了三方面优势：一是降低计算复杂度，二是增强模型泛化能力，三是实现对可变长度连续序列数据的特征提取。该机制不仅能捕捉序列特征的时空连续性，还通过位置无关的特性避免了逐位置规则学习，但保留了序列位置的识别能力。
• 尽管RNN网络在时序数据处理上表现优异，其基础结构仍存在显著缺陷。理论上RNN应具备长期记忆能力和任意长度序列处理能力，但实际应用中会出现梯度消失现象。该问题源于两方面：一是BP算法的固有缺陷（前馈神经网络中随深度增加出现训练失效），二是RNN特有的长程依赖问题（时间跨度导致记忆衰减）。从数学视角看，当激活函数导数小于1时，多层网络梯度呈指数衰减；反之若导数大于1则引发指数级梯度膨胀，造成网络失稳（即梯度爆炸问题）。
• 针对这些局限性，学界提出了两种主流改进架构：长短期记忆网络（LSTM）和门控循环单元（GRU）。

长短期记忆网络（LSTM）

• 长短期记忆网络(Long Short-Term Memory，LSTM)主要为了解决标准RNN在处理长序列数据时面临的梯度消失等问题。
• 基本的LSTM结构单元如图：
  
• 图中四个矩形即图标1，2，3，4是普通神经网络的隐藏层结构。其中$f_{(t)，i_t，o_{(}t)}$都是Logistic函数，$g_{(t)}$是Tanh函数。
• LSTM单元状态分为长时记忆和短时记忆，其中短时记忆i用向量$h_{(t)}$表示，长时记忆用$c_{(t)}$表示。
• LSTM单元结构中还有三个门限控制器：忘记门限，输入门限和输出门限。三个门限都使用Logistic函数，如果输出值为1，表示门限打开；如果输出值为0，表示门限关闭。
  • 忘记门限：主要用$f_{(t)}$控制着长时记忆是否被遗忘。
  • 输入门限：主要由$i_{(t)}$和$g_t$，$i_{(t)}$用于控制$g_t$用于增强记忆的部分。
  • 输出门限：主要由$o_{(t)}$控制应该在该时刻被读取和输出的部分。
• LSTM单元的基本流程如下：随着短时记忆$c_{(t)}$从左到右横穿整个网络，它首先经过一个遗忘门，丢弃一些记忆，然后通过输入门限来选择增加一些新记忆，最后直接输出$c_{(t)}$。此外，增加记忆这部分操作中，长时记忆先经过Tanh函数，然后被输出门限过滤，产生了短时记忆ht)。
• 综上所述，LSTM可以识别重要的输入（输入门限的作用），并将这些信息在长时记忆中存储下来，通过遗忘门保留需要的部分，以及在需要的时候能够提取它。

• LSTM单元结构中的三个门限控制器、两种状态以及输出：
  $$\begin{array}{rl}& i_{(t)}=\sigma (w_{\times i}^{\top }\cdot x_{(t)}+w_{hi}^{\top }\cdot h_{(t-1)}+b_i)\\ & f_{(t)}=\sigma (w_{\times j}^{\top }\cdot x_{(t)}+w_{hj}^{\top }\cdot h_{(t-1)}+b_f)\\ & o_{(t)}=\sigma (w_{xo}^{\top }\cdot x_{(t)}+w_{ho}^{\top }\cdot h_{(t-1)}+b_o)\\ & g_{(t)}=\mathrm{Tanh}(w_{xg}^{\top }\cdot x_{(t)}+w_{hg}^{\top }\cdot h_{(t-1)}+b_g)\\ & c_{(t)}=f_{(t)}\otimes c_{(t-1)}+i_{(t)}\otimes g_{(t)}\\ & y_{(t)}=h_{(t)}=o_{(t)}\otimes \mathrm{Tanh}(c_{(t)})\end{array}$$
• $w_{xi}、w_{xf}、w_{xo}、w_{xg}$是每一层连接到$x_{(t)}$的权重，$w_{hi}、w_{hf}、w_{ho}、w_{hg}$是每层连接到前一个短时记忆$h_{(t-1)}$的权重，$b_i、b_f、b_o、b_g$是每一层的偏置项。

门控循环单元（GRU）

• 门控循环单元（GateRecurrentUnit，GRU）是循环神经网络（RNN）的一个变种，它旨在解决标准RNN中梯度消失的问题。GRU结构更简单，效果更好。

• GRU的设计初衷是解决长期依赖问题，即标准RNN难以捕捉长序列中较早时间步的信息。通过引入更新门和重置门，GRU能够学习到何时更新或忽略某些信息，从而更好地处理序列数据。

• 相较于LSTM，GRU有更少的参数和计算复杂度，特别是在资源受限的情况下训练更快，同时也能取得不错的性能表现，。GRU已被广泛应用于各种序列建模任务，如语言模型、机器翻译、语音识别等领域。

• GRU如图所示：
  

• GRU中包含三个激活函数，分别为Logistic、Logistic、Tanh函数。

• 如图所示，GRU通过精简门控机制提升了计算效率，其核心特征如下：

1. 门控结构简化：

   • 采用**重置门（r）和更新门（z）**双门架构，激活函数缩减至3个（使用Sigmoid或Logistic函数，输出0~1的门控信号）。
   • 合并状态向量为单一隐藏状态$h_t$，简化信息流动路径。

2. 门控功能详解：

   • 重置门（r）：控制前一时刻隐藏状态$h_{t-1}$对当前候选状态的影响程度。门值越接近0，丢弃的历史信息越多，主层（如Tanh激活单元）将更多依赖当前输入 $x_t$ 重新计算候选状态。
   • 更新门（z）：调节 $h_{t-1}$ 传递至当前状态 $h_t$ 的比例。门值越接近1，保留的历史信息比例越高，新生成的信息比例越低。

3. 工作流程：

   • 步骤1：根据 $h_{t-1}$ 和 $x_t$ 计算重置门 $r_t$ 和更新门 $z_t$。
   • 步骤2：利用 $r_t$ 重置 $h_{t-1}$，生成候选状态 ${\tilde{h}}_t$（通常通过Tanh激活）。
   • 步骤3：通过 $z_t$ 加权融合 $h_{t-1}$ 与 ${\tilde{h}}_t$，输出最终状态 $h_t$。

• GRU单元结构的计算过程：
  $$\begin{array}{rl}& z_{(t)}=\sigma (w_{xz}^{\mathrm{T}}\cdot x_{(t)}+w_{hz}^{\mathrm{T}}\cdot h_{(t-1)})\\ & r_{(t)}=\sigma (w_{xr}^{\mathrm{T}}\cdot x_{(t)}+w_{hr}^{\mathrm{T}}\cdot h_{(t-1)})\\ & g_{(t)}=\mathrm{Tanh}(w_{xg}^{\mathrm{T}}\cdot x_{(t)}+w_{hg}^{\mathrm{T}}\cdot (r_{(t)}\otimes h_{(t-1)}))\\ & h_{(t)}=(1-z_{(t)})\otimes \mathrm{Tanh}(w_{xg}^{\mathrm{T}}\cdot h_{(t-1)}+z_{(t)}\otimes g_{(t)})\end{array}$$
• $w_{xz}、w_{xr}$ 和$w_{xg}$是每一层连接到输入$x(t)$的权重，$W_{hz}、W_{hr},$和$W_{hg}$ 是每一层连接到前一个短时记忆$h_{(t-1)}$的权重。