pytorch 14.3 Batch Normalization综合调参实践-EW帮帮网

文章目录

一、Batch Normalization与Batch_size综合调参

我们知道，BN是一种在长期实践中被证明行之有效的优化方法，但在使用过程中首先需要知道，BN的理论基础（尽管不完全正确）是以BN层能够有效预估输入数据整体均值和方差为前提的，如果不能尽可能的从每次输入的小批数据中更准确的估计整体统计量，则后续的平移和放缩也将是有偏的。而由小批数据估计整体统计量的可信度其实是和小批数据本身数量相关的，如果小批数据数量太少，则进行整体统计量估计时就将有较大偏差，此时会影响模型准确率。
因此，一般来说，我们在使用BN时，至少需要保证小批数据量（batch_size)在15-30以上，才能进行相对准确的预估。此处我们适当调整小批数据量参数，再进行模型计算。

# 进行数据集切分与加载
# 设置batch_size为50
train_loader, test_loader = split_loader(features, labels, batch_size=50)

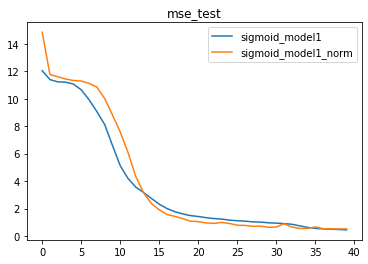
在这里插入图片描述

我们发现，当提升batch_size之后，带BN层的模型效果有明显提升，相比原始模型，带BN层的模型拥有更快的收敛速度。

二、复杂模型上的Batch_normalization表现

1、BN对复杂模型（sigmoid）的影响

一般来说，BN方法对于复杂模型和复杂数据会更加有效，换而言之，很多简单模型是没必要使用BN层（徒增计算量）。对于上述net_class1来说，由于只存在一个隐藏层，因此也不会存在梯度不平稳的现象，而BN层的优化效果也并不明显。接下来，我们尝试构建更加复杂的模型，来测试BN层的优化效果。

从另一个角度来说，其实我们是建议更频繁的使用更加复杂的模型并带上BN层的，核心原因在于，复杂模型带上BN层之后会有更大的优化空间。

接下来，我们尝试设置更加复杂的数据集，同时增加模型复杂度，测试在更加复杂的环境下BN层表现情况。
此处我们创建满足 $y=2x_1^2-x_2^2+3x_3^2+x_4^2+2x_5^2$ 的回归类数据集。

# 设置随机数种子
torch.manual_seed(420)  

# 创建最高项为2的多项式回归数据集
features, labels = tensorGenReg(w=[2, -1, 3, 1, 2], bias=False, deg=2)

# 进行数据集切分与加载
train_loader, test_loader = split_loader(features, labels, batch_size=50)

接下来，我们同时创建Sigmoid1-4，并且通过对比带BN层的模型和不带BN层的模型来进行测试。

# class1对比模型
# 设置随机数种子
torch.manual_seed(24)  

# 实例化模型  
sigmoid_model1 = net_class1(act_fun= torch.sigmoid, in_features=5)
sigmoid_model1_norm = net_class1(act_fun= torch.sigmoid, in_features=5, BN_model='pre')

# 创建模型容器
model_ls1 = [sigmoid_model1, sigmoid_model1_norm]           
name_ls1 = ['sigmoid_model1', 'sigmoid_model1_norm']

# 核心参数
lr = 0.03
num_epochs = 40

# 模型训练
train_ls1, test_ls1 = model_comparison(model_l = model_ls1, 
                                       name_l = name_ls1, 
                                       train_data = train_loader,
                                       test_data = test_loader,
                                       num_epochs = num_epochs, 
                                       criterion = nn.MSELoss(), 
                                       optimizer = optim.SGD, 
                                       lr = lr, 
                                       cla = False, 
                                       eva = mse_cal)


# class2对比模型
# 设置随机数种子
torch.manual_seed(24)  

# 实例化模型  
sigmoid_model2 = net_class2(act_fun= torch.sigmoid, in_features=5)
sigmoid_model2_norm = net_class2(act_fun= torch.sigmoid, in_features=5, BN_model='pre')

# 创建模型容器
model_ls2 = [sigmoid_model2, sigmoid_model2_norm]           
name_ls2 = ['sigmoid_model2', 'sigmoid_model2_norm']

# 核心参数
lr = 0.03
num_epochs = 40

# 模型训练
train_ls2, test_ls2 = model_comparison(model_l = model_ls2, 
                                       name_l = name_ls2, 
                                       train_data = train_loader,
                                       test_data = test_loader,
                                       num_epochs = num_epochs, 
                                       criterion = nn.MSELoss(), 
                                       optimizer = optim.SGD, 
                                       lr = lr, 
                                       cla = False, 
                                       eva = mse_cal)

# class3对比模型
# 设置随机数种子
torch.manual_seed(24)  

# 实例化模型  
sigmoid_model3 = net_class3(act_fun= torch.sigmoid, in_features=5)
sigmoid_model3_norm = net_class3(act_fun= torch.sigmoid, in_features=5, BN_model='pre')

# 创建模型容器
model_ls3 = [sigmoid_model3, sigmoid_model3_norm]           
name_ls3 = ['sigmoid_model3', 'sigmoid_model3_norm']

# 核心参数
lr = 0.03
num_epochs = 40

# 模型训练
train_ls3, test_ls3 = model_comparison(model_l = model_ls3, 
                                       name_l = name_ls3, 
                                       train_data = train_loader,
                                       test_data = test_loader,
                                       num_epochs = num_epochs, 
                                       criterion = nn.MSELoss(), 
                                       optimizer = optim.SGD, 
                                       lr = lr, 
                                       cla = False, 
                                       eva = mse_cal)

# class4对比模型
# 设置随机数种子
torch.manual_seed(24)  

# 实例化模型  
sigmoid_model4 = net_class4(act_fun= torch.sigmoid, in_features=5)
sigmoid_model4_norm = net_class4(act_fun= torch.sigmoid, in_features=5, BN_model='pre')

# 创建模型容器
model_ls4 = [sigmoid_model4, sigmoid_model4_norm]           
name_ls4 = ['sigmoid_model4', 'sigmoid_model4_norm']

# 核心参数
lr = 0.03
num_epochs = 40

# 模型训练
train_ls4, test_ls4 = model_comparison(model_l = model_ls4, 
                                       name_l = name_ls4, 
                                       train_data = train_loader,
                                       test_data = test_loader,
                                       num_epochs = num_epochs, 
                                       criterion = nn.MSELoss(), 
                                       optimizer = optim.SGD, 
                                       lr = lr, 
                                       cla = False, 
                                       eva = mse_cal)

# 训练误差
plt.subplot(221)
for i, name in enumerate(name_ls1):
    plt.plot(list(range(num_epochs)), train_ls1[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train_ls1')

plt.subplot(222)
for i, name in enumerate(name_ls2):
    plt.plot(list(range(num_epochs)), train_ls2[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train_ls2')

plt.subplot(223)
for i, name in enumerate(name_ls3):
    plt.plot(list(range(num_epochs)), train_ls3[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train_ls3')

plt.subplot(224)
for i, name in enumerate(name_ls4):
    plt.plot(list(range(num_epochs)), train_ls4[i], label=name)
plt.legend(loc = 1)
plt.title('mse_train_ls4')

# 训练误差
plt.subplot(221)
for i, name in enumerate(name_ls1):
    plt.plot(list(range(num_epochs)), test_ls1[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test_ls1')

plt.subplot(222)
for i, name in enumerate(name_ls2):
    plt.plot(list(range(num_epochs)), test_ls2[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test_ls2')

plt.subplot(223)
for i, name in enumerate(name_ls3):
    plt.plot(list(range(num_epochs)), test_ls3[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test_ls3')

plt.subplot(224)
for i, name in enumerate(name_ls4):
    plt.plot(list(range(num_epochs)), test_ls4[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test_ls4')

在这里插入图片描述

由此，我们可以清楚的看到，BN层对更加复杂模型的优化效果更好。换而言之，越复杂的模型对于梯度不平稳的问题就越明显，因此BN层在解决该问题后模型效果提升就越明显。

2、模型复杂度对模型效果的影响

并且，针对复杂数据集，在一定范围内，伴随模型复杂度提升，模型效果会有显著提升。但是，当模型太过于复杂时，仍然会出现模型效果下降的问题。

for i, name in enumerate(name_ls1):
    plt.plot(list(range(num_epochs)), test_ls1[i], label=name)
for i, name in enumerate(name_ls2):
    plt.plot(list(range(num_epochs)), test_ls2[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')

for i, name in enumerate(name_ls2):
    plt.plot(list(range(num_epochs)), test_ls2[i], label=name)
for i, name in enumerate(name_ls4):
    plt.plot(list(range(num_epochs)), test_ls4[i], label=name)
plt.legend(loc = 1)
plt.title('mse_test')

在这里插入图片描述

3、BN对复杂模型（tanh）的影响

对于Sigmoid来说，BN层能很大程度上缓解梯度消失问题，从而提升模型收敛速度，并且小幅提升模型效果。而对于激活函数本身就能输出Zero-Centered结果的tanh函数，BN层的优化效果会更好。
训练结果：
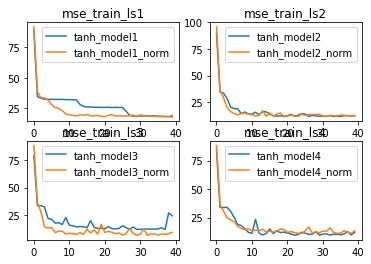
在这里插入图片描述
测试结果：

相比Sigmoid，使用tanh激活函数本身就是更加复杂的一种选择，因此，BN层在tanh上所表现出的更好的优化效果，也能看成是BN在复杂模型上效果有所提升。

三、包含BN层的神经网络的学习率优化

1.学习率敏感度

学习率lr对复杂模型（tanh）的影响

# 学习率 0.1
# 学习率 0.03
# 学习率 0.01
# 学习率 0.005

在这里插入图片描述
能够看出，随着学习率逐渐变化，拥有BN层的模型表现出更加剧烈的波动，这也说明拥有BN层的模型对学习率变化更加敏感。

2.学习率学习曲线

对于学习率的调整，一般都会出现倒U型曲线。我们能够发现，在当前模型条件下，学习率为0.005左右时模型效果较好。当然，我们这里也只取了四个值进行测试，也有可能最佳学习率在0.006或者0.0051，关于学习率参数的调整策略（LR-scheduler），我们将在下一节进行详细介绍，本节我们将利用此处实验得到的0.005作为学习率进行后续实验。
tanh_model3在不同学习率lr下的loss值
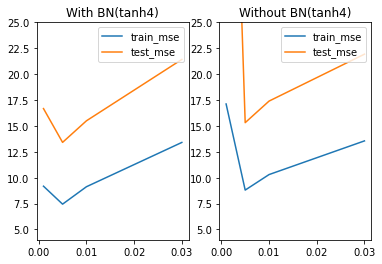
在这里插入图片描述

3.不同学习率下不同模型优化效果

既然学习率学习曲线是U型曲线，那么U型的幅度其实就代表着学习率对于该模型的优化空间，这里我们可以通过简单实验，来观测不同模型的U型曲线的曲线幅度。首先，对于tanh2来说，带BN层的模型学习率优化效果比不带BN层学习率优化效果更好。

# 设置随机数种子
torch.manual_seed(24)  

# 实例化模型  
tanh_model3 = net_class3(act_fun= torch.tanh, in_features=5)
tanh_model3_norm = net_class3(act_fun= torch.tanh, in_features=5, BN_model='pre')
tanh_model4 = net_class4(act_fun= torch.tanh, in_features=5)
tanh_model4_norm = net_class4(act_fun= torch.tanh, in_features=5, BN_model='pre')
     
# 创建模型容器
model_l = [tanh_model3, tanh_model3_norm, tanh_model4, tanh_model4_norm]           
name_l = ['tanh_model3', 'tanh_model3_norm', 'tanh_model4', 'tanh_model4_norm']

# 核心参数
lr = 0.001
num_epochs = 40

# 模型训练 tanh_model3
train_l001, test_l001 = model_comparison(model_l = model_l, 
                                         name_l = name_l, 
                                         train_data = train_loader,
                                         test_data = test_loader,
                                         num_epochs = num_epochs, 
                                         criterion = nn.MSELoss(), 
                                         optimizer = optim.SGD, 
                                         lr = lr, 
                                         cla = False, 
                                         eva = mse_cal)

lr_l = [0.03, 0.01, 0.005, 0.001]
train_ln = [train_l03[1:,-5:].mean(), train_l01[1:,-5:].mean(), train_l005[1:,-5:].mean(), train_l001[1:,-5:].mean()]
test_ln = [test_l03[1:,-5:].mean(), test_l01[1:,-5:].mean(), test_l005[1:,-5:].mean(), test_l001[1:,-5:].mean()]
train_l = [train_l03[0:,-5:].mean(), train_l01[0:,-5:].mean(), train_l005[0:,-5:].mean(), train_l001[0:,-5:].mean()]
test_l = [test_l03[0:,-5:].mean(), test_l01[0:,-5:].mean(), test_l005[0:,-5:].mean(), test_l1[0:,-5:].mean()]

plt.subplot(121)
plt.plot(lr_l, train_ln, label='train_mse')
plt.plot(lr_l, test_ln, label='test_mse')
plt.legend(loc = 1)
plt.ylim(4, 25)
plt.title('With BN(tanh3)')

plt.subplot(122)
plt.plot(lr_l, train_l, label='train_mse')
plt.plot(lr_l, test_l, label='test_mse')
plt.legend(loc = 1)
plt.ylim(4, 25)
plt.title('Without BN(tanh3)')

在这里插入图片描述

四、带BN层的神经网络模型综合调整策略总结

最后，我们总结下截至目前，针对BN层的神经网络模型调参策略。

简单数据、简单模型下不用BN层，加入BN层效果并不显著；

BN层的使用需要保持running_mean和running_var的无偏性，因此需要谨慎调整batch_size；

学习率是重要的模型优化的超参数，一般来说学习率学习曲线都是U型曲线；

从学习率调整角度出发，对于加入BN层的模型，学习率调整更加有效；对于带BN层模型角度来说，BN层能够帮助模型拓展优化空间，使得很多优化方法都能在原先无效的模型上生效；

对于复杂问题，在计算能力能够承担的范围内，应当首先构建带BN层的复杂模型，然后再试图进行优化，就像上文所述，很多优化方法只对带BN层的模型有效；

其他拓展方面结论：

关于BN和Xavier/Kaiming方法，一般来说，使用BN层的模型不再会用参数初始化方法，从理论上来看添加BN层能够起到参数初始化的相等效果；（另外，带BN层模型一般也不需要使用Dropout方法）

本节尚未讨论ReLU激活函数的优化，相关优化方法将放在后续进行详细讨论，但需要知道的是，对于ReLU叠加的模型来说，加入BN层之后能够有效缓解Dead
ReLU Problem，此时无须刻意调小学习率，能够在收敛速度和运算结果间保持较好的平衡。

BN层是目前大部分深度学习模型的标配，但前提是你有能力去对其进行优化；

pytorch 14.3 Batch Normalization综合调参实践