一、介绍
遥感目标检测 RSDet 是四边形检测器,而且都考虑到了顺序标签点(sequential label points)的问题。
- https://arxiv.org/abs/1911.08299
我们首先介绍两种主流的边界框参数化协议,即五参数模型和八参数模型。然后,我们正式识别了五参数系统中旋转角度的不连续性及其导致的宽高突变。此外,我们定量地展示了五参数系统中由不同测量单位引起的回归不一致性带来的负面影响。我们将这些问题统称为旋转敏感误差 ( Rotation Sensitivity Error,RSE),并提出了一种针对五参数系统的调制旋转损失函数,以实现更平滑的学习。我们进一步指出,即使是改进的八参数系统仍然存在损失不连续性的问题,然后为八参数系统设计了相应的调制旋转损失函数。
(一)五参数检测方法( 基于角度)
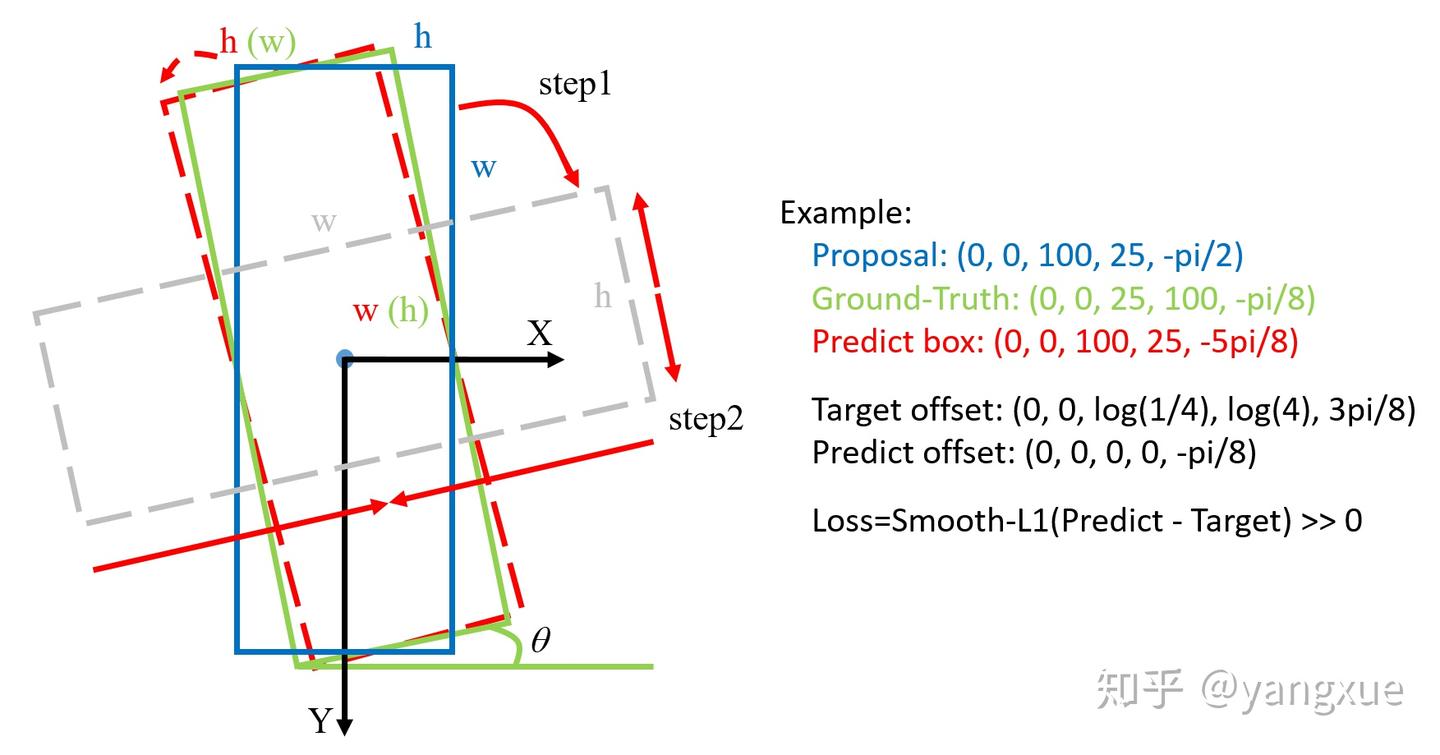
在当前常用的旋转检测框的角度定义下,由于存在旋转角度的边界问题,会产生不必要的损失!
(二)八参数检测方法(point-based)的边界
如果是蓝框是anchor,红框是ground-truth,那么通过点的排序之后,实际和理想的回归方式是一样的(按照回归的距离定义)

(三)五参数检测的调制旋转损失
损失不连续性仅发生在边界情况下,如图 6a 所示。在本文中,我们设计了以下边界约束来调节损失,称为
调制旋转损失 lmr


其中,lcp 是中心点损失。
lmr 中的第一项是lcp。第二项是用于使损失连续的校正,它通过消除角度周期性和高宽可互换性来实现。这种校正可以看作是关于突变位置的对称性。最后, 取校正中的最小值。
在实际应用中,通常使用边界框回归的相对值来避免不同尺度的物体造成的误差。


(四)八参数检测的调制旋转损失
为了避免固有的回归不一致性,最近开发了八参数表示 [42,46, 47]。具体而言,基于八参数回归的检测器直接对物体的四个角进行回归,因此预测结果为四边形。四边形回归的关键步骤是预先对四个角点进行排序,这样即使姿态预测正确,也能避免很大的损失。对于顶点顺序,我们采用基于叉积的算法来获取四个顶点的序列,详见算法 1。
几何排序:
- 采用叉积算法对预测角点强制排序:
- 确定最左侧点(水平矩形时取上方点);
- 通过叉乘找到对角点;
- 按顺时针/逆时针顺序确定剩余点

需要注意的是,该算法适用于凸四边形,并且我们在这里使用顺时针顺序进行输出,且不失一般性。算法 1 与深度匹配先验网络 [46] 中提出的算法类似。
然而,八参数回归模型中仍然存在损失不连续性。

例如,我们可以假设一个真实框可以用角点序列 a → b → c → d 来描述(见图 2 中的红色框)。然而,当真实框稍微旋转一个小角度时,角点序列就变成了 d → a → b → c(见图 2 中的绿色框)。因此,考虑边界情况下的八参数回归的情况,如图 4b 所示。

从蓝色参考框到绿色真实框的实际回归过程是 {(a → a), (b → b), (c → c), (d → d)},但显然理想的回归过程应该是 {(a → b), (b → c), (c → d), (d → a)}。这种情况也导致了模型训练困难和回归不平滑。
这里,我们设计了八参数版本的调制旋转损失函数,它由三部分组成:
i) 将预测框的四个顶点顺时针移动一位;
ii) 保持预测框顶点的顺序不变;
iii) 将预测框的四个顶点逆时针移动一位;
iv) 取上述三种情况下的最小值。
消除了旋转检测中回归不一致性和损失不连续性的问题。

| 方法 | 关键点表示 | 顺序控制策略 | 边界问题解决方案 |
|---|---|---|---|
| Gliding Vertex | 水平框+偏移比例 | 固定水平框顶点顺序 | 倾斜因子过滤近水平目标 |
| RSDet | 直接回归排序角点 | 几何排序算法+调制损失 | 多候选匹配+损失归一化 |
两者的设计均针对旋转目标检测的挑战,Gliding Vertex通过间接回归简化问题,而RSDet通过损失函数优化直接处理角点顺序。
附录:真值设计

例如,我们可以假设一个真实框可以用角点序列 a → b → c → d 来描述(见图 2 中的红色框)。然而,当真实框稍微旋转一个小角度时,角点序列就变成了 d → a → b → c(见图 2 中的绿色框)