数据结构第七章（五）-散列表

散列表

一、散列表的基本概念

1.散列表、散列函数

散列表（哈希表，Hash Table）：是一种数据结构。特点是：可以根据数据元素的关键字计算出它在散列表中的存储地址；

散列函数（哈希函数）：Addr = H(key) 建立了“关键字”——>“存储地址”的映射关系。

其实简单来说散列表就是一个可以通过计算算出来存放在哪个位置的表，然后散列函数就是你计算出来是咋计算的，没有那么高大上。举个栗子就懂了：

如果某散列表的长度为13，散列函数 H(key) = key%13。依次将数据元素 19、14、23插入散列表:

19%13=6，所以“19”应该放在下标为“6”的地方；
14%13=1，所以“14”应该放在下标为“1”的地方；
23%13=10，所以“23”应该放在下标为“10”的地方

即：

理想情况下，在散列表中查找一个元素的时间复杂度为O(1)。

比如：

查找元素 19：根据散列函数计算出元素的存储地址=19%13=6，检查位置#6，查找成功；
查找元素 16：根据散列函数计算出元素的存储地址=16%13=3，检查位置#3，查找失败；

理想情况下，不需要干什么，算出下标直接去就vans了。

2.冲突、同义词

但是理想很丰满，现实很骨感，我们现实肯定不是上面说的那样美好。
比如像刚刚那个散列表，如果我们还想再将元素“1”插入散列表，那么计算插入的下标： 1%13=1，但是这个时候我们发现下标1所在的位置已经有人了，所以我们就“冲突”了。

冲突（碰撞）：在散列表中插入一个数据元素时，需要根据关键字的值确定其存储地址，若该地址已经存储了其他元素，则称这种情况为“冲突（碰撞）”

同义词：若不同的关键字通过散列函数映射到同一个存储地址，则称它们为“同义词”

对于散列函数 H(key)=key%13 来说，1和14是“同义词”。

那么我们发生了冲突，如何减少冲突就是我们要做的事情了。对于我们的散列函数 H(key)=key%13 来说，1和14是“同义词”，那么换个散列函数不就行了？

比如我们把散列函数改为 H(key)=key%12 ，则就不发生冲突了，因为：

19%12=7，所以“19”应该放在下标为“7”的地方；
14%12=2，所以“14”应该放在下标为“2”的地方；
23%12=11，所以“23”应该放在下标为“11”的地方；
1%12=1，所以“1”应该放在下标为“1”的地方

so构造更合适的散列函数，可以让各个关键字尽可能地映射到不同的存储位置，从而减少冲突。

所以我们下面就要接着说如何构造散列函数了。

但！是！

如果“冲突”无可避免，也就是我们就要用这个散列函数，就不换，怎么都不换，那我们如何处理冲突？
这就是我们最后要说的处理冲突的方法了，俩，一个拉链法一个开放定址法。

拉链法（又称链接法、链地址法）：把所有“同义词”存储在一个链表中；开放定址法：如果发生“冲突”，就给新元素找另一个空闲位置，这个“另一个空闲位置”的找取也有不同的方法。

这些会细说，但是也要宏观了解一下。

二、散列函数的构造

我们先来说说如何构造散列函数（即关键字——>散列地址的映射），我们的精神非常健康，我们的目的只有一个，就是散列函数要尽可能地减少“冲突”。

那么设计散列函数时应该注意什么？

• 定义域必须涵盖所有可能出现的关键字；
• 值域不能超出散列表的地址范围；
• 尽可能地减少冲突。散列函数计算出来的地址应尽可能均匀分布在整个地址空间；
• 散列函数应尽量简单，能够快速计算出任意一个关键字对应的散列地址。

比如，散列表长度为13，关键字可能是任一“整数”

第1条是说散列函数不能设置为诸如 H(key) = √key % 13，因为我们关键字是任一整数，这样设计关键字就不能为负值了；

第2条是说散列函数不能设置为诸如 H(key) = key % 15，因为这样可能被映射到非法地址 13、14；

第3条是说散列函数不能设置为诸如 H(key) = (key * 13) % 13，因为这样任何关键字都会被映射到地址0；

第4条是说散列函数不能设置为诸如 H(key) = (key! ) % 13，因为这样若关键字值较大，计算阶乘耗时就比较高了，比如10000！你怎么算，是吧。

那我们来构造散列函数：

1.除留余数法

除留余数法，我们看它的名字，这可不是白起的。人如其名，其实就是除以一个数把它的余数留下来当地址的方法。

- 除留余数法—— H(key) = key % p

散列表表长为m，取一个不大于m但最接近或等于m的质数p

还记得什么是质数吗？质数又称素数。指除了1和此整数自身外，不能被其他自然数整除的数，比如5只能被1和自身5整除，所以5是质数；4不知能被1和自身4整除，还能被2整除，所以是合数。

但我们为什么要取质数呢？因为对质数取余，可以分布更均匀，从而减少冲突。

举个栗子，比如可能出现的关键字={2，4，6，8，10，12，14}，散列表表长为8.

两个散列函数，一个是 H(key) = key % 8，一个是 H(key) = key % 7，那么结果就是如下图所示：

左边是模合数，右边是模质数，可以看到模质数分布更均匀。but……why？？？这就要追溯到《数论》了，《数论》里面说，取余运算会被“公因子”影响。啊，计算机的尽头是数学，数学的尽头是玄学，一步到位，我直接原地出家。

除留余数法的适用场景：较为通用，只要关键字是整数即可。

比如一个散列表表长 m=13，13是质数，因此可以直接令散列函数 H(key) = key%13；再比如一个散列表表长 m=15，不大于15且最接近15的质数是13，因此可以令散列函数 H(key) = key%13（这样会有两个下标14、15用不到，不过没关系，我们要的是平均。）

这个除留余数法是最常用的了。

2.直接定址法

直接定址法，人如其名，就是直接确定地址的方法，算的比较简单，什么加减之类的。

- 直接定址法—— H(key) = key 或 H(key) = a * key + b

其中 a，b是常数。这种方法计算最简单，且不会产生冲突。若关键字分布不连续，空位较多，则会造成存储空间的浪费。

适用场景：关键字分布基本连续

啥是关键字分布基本连续？比如用散列表存储某班级的30个学生信息，班内学生学号为 (1125112176~1125112205），可令 H(key) = key - 1125112176，因为这样就可以映射到下标 0到29 上，且不会冲突。

3.数字分析法

数字分析法，这个有点抽象，是选几个位的数字来当做它的地址。

- 数字分析法—— 选取数码分布较为均匀的若干位作为散列地址

设关键字是 r 进制数（如十进制数），而 r 个数码在各位上出现的频率不一定相同，可能在某些位上分布均匀一些，每种数码出现的机会均等；而在某些位上分布不均匀，只有某几种数码经常出现，此时可选取数码分布较为均匀的若干位作为散列地址。

什么意思呢？就是比如我们去营业厅新办一个手机卡，要选一个手机号，它会给你在屏幕上出很多个号码，仔细看都是一个号段里面的号码，一般只有后四位不同（如果后四位也相同那不就重复了嘛），相对于其他位来说，后四位分布比较均匀，所以我们就可以用后四位来作为映射地址。

适用场景：关键字集合已知，且关键字的某几个数码位分布均匀

eg：要求将手机用户的信息存入长度为 10000 的散列表，以“手机号码”作为关键字设计散列函数

此时我们就以手机号后四位作为散列地址。

4.平方取中法

平方取中法，人如其名，就是给它平方，再取平方后中间的几位数。

- 平方取中法—— 取关键字的平方值的中间几位作为散列地址

什么意思呢？就是比如关键字是1234，那么它的平方就是1522756，再抽取中间的3位就是227，用做散列地址。再比如关键字是4321，那么它的平方就是18671041，抽取中间的3位就可以是67用做散列地址。平方取中法比较适合于不知道关键字的分布，而位数又不是很大的情况。

具体取多少位要视实际情况而定。这种方法得到的散列地址与关键字的每位都有关系，因此使得散列地址分布比较均匀。

因为我们取平方不就是它俩相乘吗，相乘就是每位数乘再错位相加，所以和每一位都有关。

适用场景：关键字的每位取值都不够均匀（其实就是不知道关键字的分布了）

三、处理冲突的方法

还记得我们之前说的吗？有的时候“冲突”是无可避免的。虽然构造更合适的散列函数可以减少冲突，但是我们就要用这个不合适的散列函数，即使不合适也不换，就不换，怎么都不换——

那我们这个时候该如何处理冲突？

1.拉链法

拉链法（又称链接法、链地址法）：把所有“同义词”存储在一个链表中。

什么意思呢？就是如果我们要把关键字 “b” 放入散列表里，但是我们通过散列函数得到的地址里面已经有关键字 “a” 了，所以我们就把 “b” 当做 “a” 的下一个结点链接起来。

1.1 插入

举个栗子，比如如果散列表长度为 13 ，散列函数 H(key) = key % 13，用拉链法解决冲突。依次插入关键字 {19， 14， 23， 1， 68， 20， 84， 27， 55， 11， 10， 79 }

so问题来了，我们如何在散列表（拉链法解决冲突）中插入一个新元素？

• 结合散列函数计算新元素的散列地址
• 将新元素插入到散列地址对应的链表（可用头插法，也可用尾插法）

看下面这个图，这是我们的散列表，里面存放的可以视为13个链表的头指针：

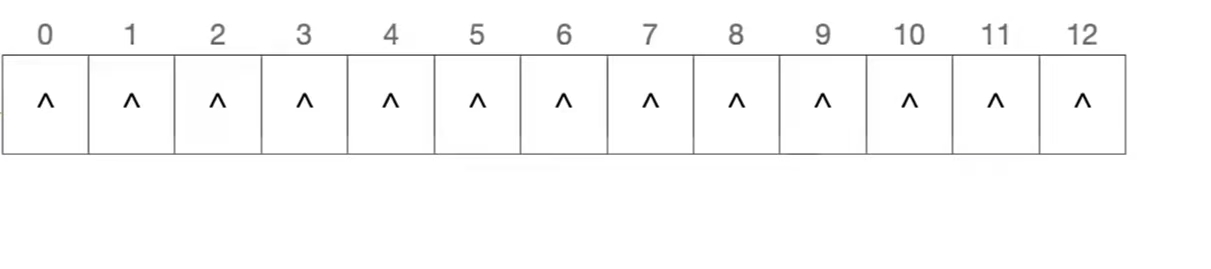
我们现在先计算一波：

19 % 13 = 6
14 % 13 = 1
23 % 13 = 10

然后我们将元素插入到散列地址对应的链表中（默认头插法），即：

我们再计算一波：

1 % 13 = 1
68 % 13 = 3
20 % 13 = 7

我们看到关键字 “1” 应该插入的位置已经有人了，所以我们用头插法插入它的前面，即：

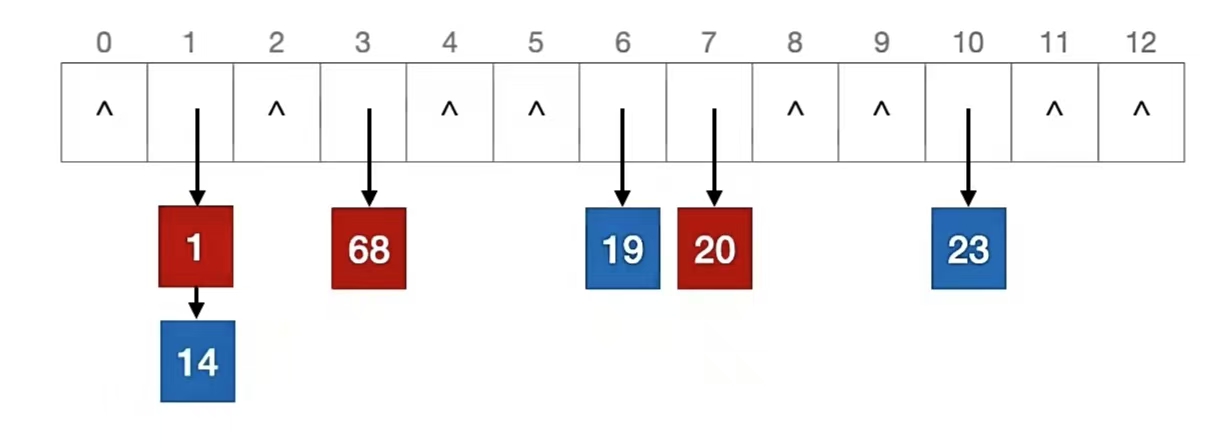
我们再再计算一波：

84 % 13 = 6
27 % 13 = 1
55 % 13 = 3

我们看到关键字 “84” 、关键字 “27”、关键字 “55” 应该插入的位置都已经有人了，所以我们用头插法插入它们的前面，即：

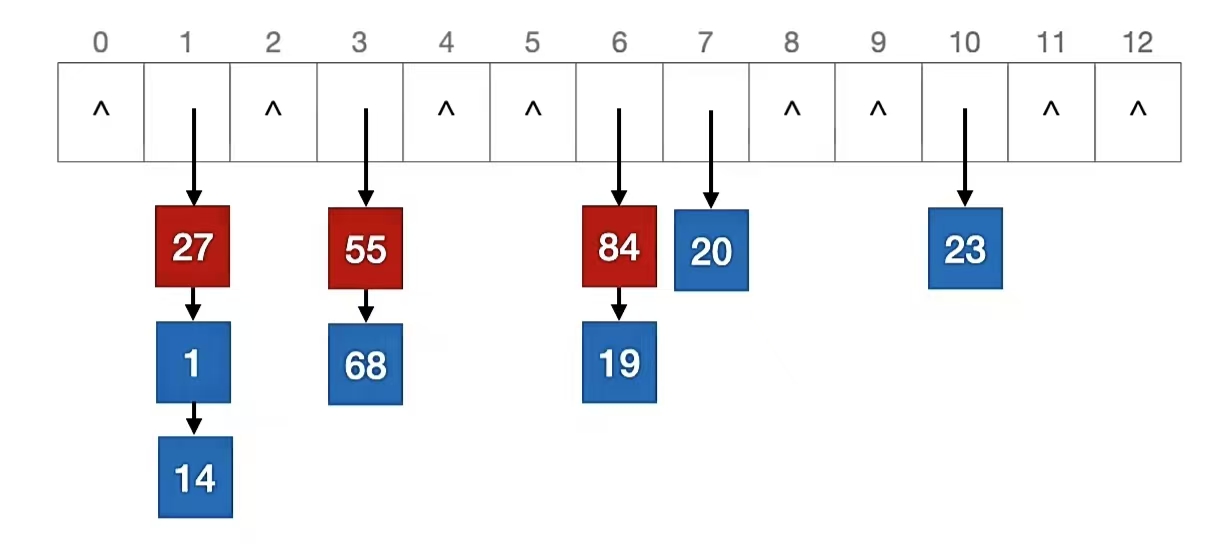
我们再再再计算一波：

11 % 13 = 11
10 % 13 = 10
79 % 13 = 1

我们看到关键字 “11” 、关键字 “10”、关键字 “79” 应该插入的位置都已经有人了，所以我们用头插法插入它们的前面，即：

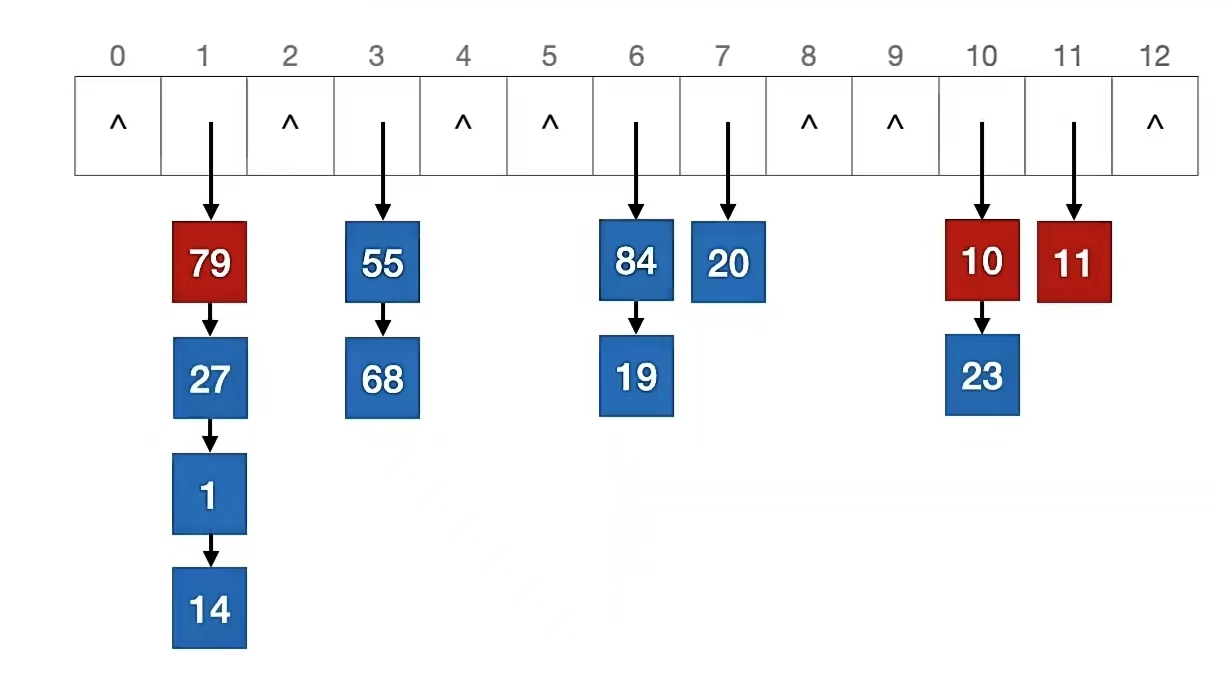
我们用拉链法就插入完成了。

1.2 查找

我们用一个栗子来说，比如如果散列表长度为 13 ，散列函数 H(key) = key % 13，用拉链法解决冲突。在下列散列表中依次查找元素 27， 20， 66， 21

散列表如下：

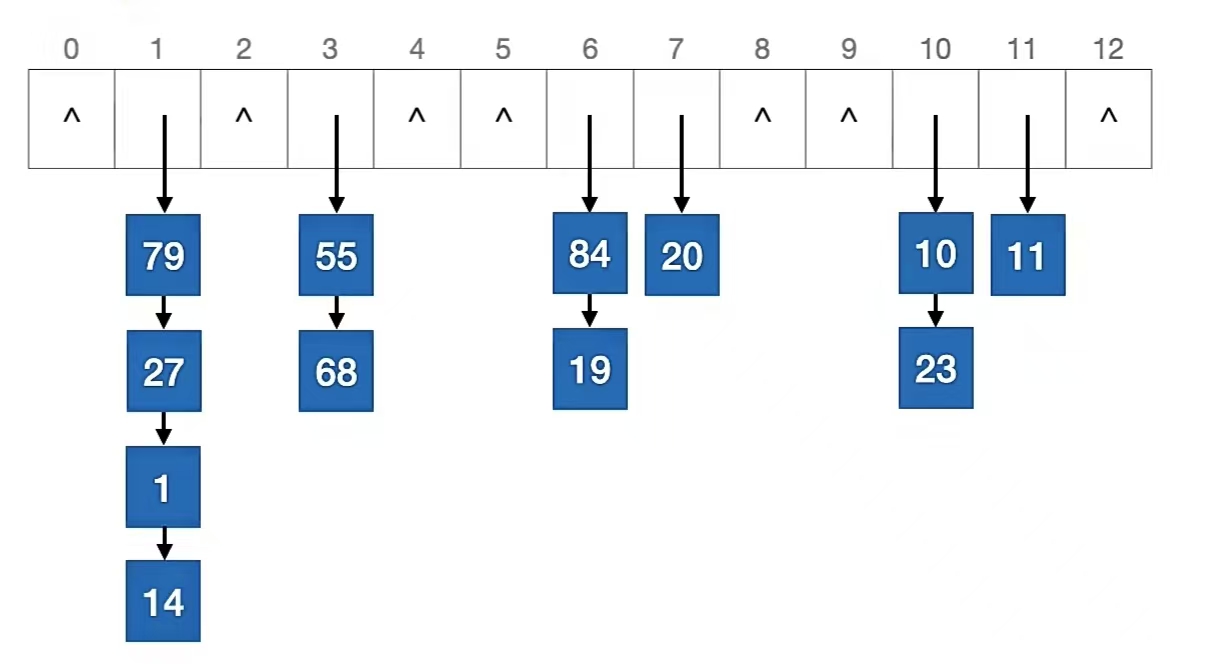
我们现在来分析每次查找操作的过程和查找长度（回忆一下：查找长度——在查找运算中，需要对比关键字的次数称为查找长度）：

首先我们查找元素 27 ，查找首先要计算目标元素存储地址：27 % 13 = 1，所以我们要在地址为“1”的地方从上往下捋。

第一个是“79”，不是；下一个是“27”，是，我们找到了，所以27查找成功，查找长度 = 2（我们对比了2次）

其次我们查找元素 20 ，查找首先要计算目标元素存储地址：20 % 13 = 7，所以我们要在地址为“7”的地方从上往下捋。

第一个是“20”，是，我们找到了，所以20查找成功，查找长度 = 1（我们对比了1次）

然后我们查找元素 66 ，查找首先要计算目标元素存储地址：66 % 13 = 1，所以我们要在地址为“1”的地方从上往下捋。

第一个是“79”，不是；下一个是“27”，不是；再下一个是“1”，不是；最后是“14”，也不是。我们没找到，所以66查找失败，查找长度 = 4（我们对比了4次）

最后我们查找元素 21 ，查找首先要计算目标元素存储地址：21 % 13 = 8，所以我们要在地址为“8”的地方从上往下捋。

这就和前面的不一样了，我们发现地址为“8”里面是空指针NULL，所以里面没有元素，所以21查找失败，查找长度 = 0（我们没有对比）

当然，有的教材会把“空指针”的对比也计入查找长度，但考试中默认只统计“关键字对比次数”。

1.3 删除

我们还用一个栗子来说。比如如果散列表长度为 13 ，散列函数 H(key) = key % 13，用拉链法解决冲突。在下列散列表中依次删除元素 27， 20， 66

首先我们来删除“27”，删除首先要找到它才能删，找到它首先要计算目标元素存储地址：27 % 13 = 1，所以我们要在地址为“1”的地方从上往下捋，找到它再删除它

“27”查找成功，所以我们删掉它。删除成功，如下所示：

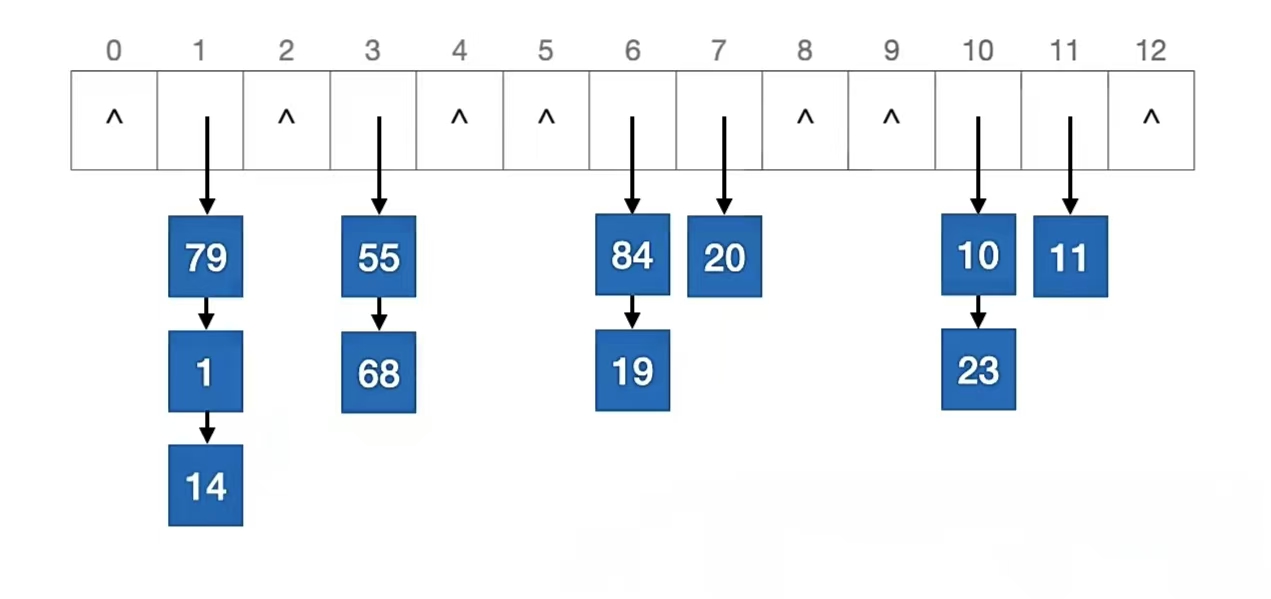
其次我们来删除“20”，删除首先要找到它才能删，找到它首先要计算目标元素存储地址：20 % 13 = 7，所以我们要在地址为“7”的地方从上往下捋，找到它再删除它

“20”查找成功，所以我们删掉它。删除成功，如下所示：

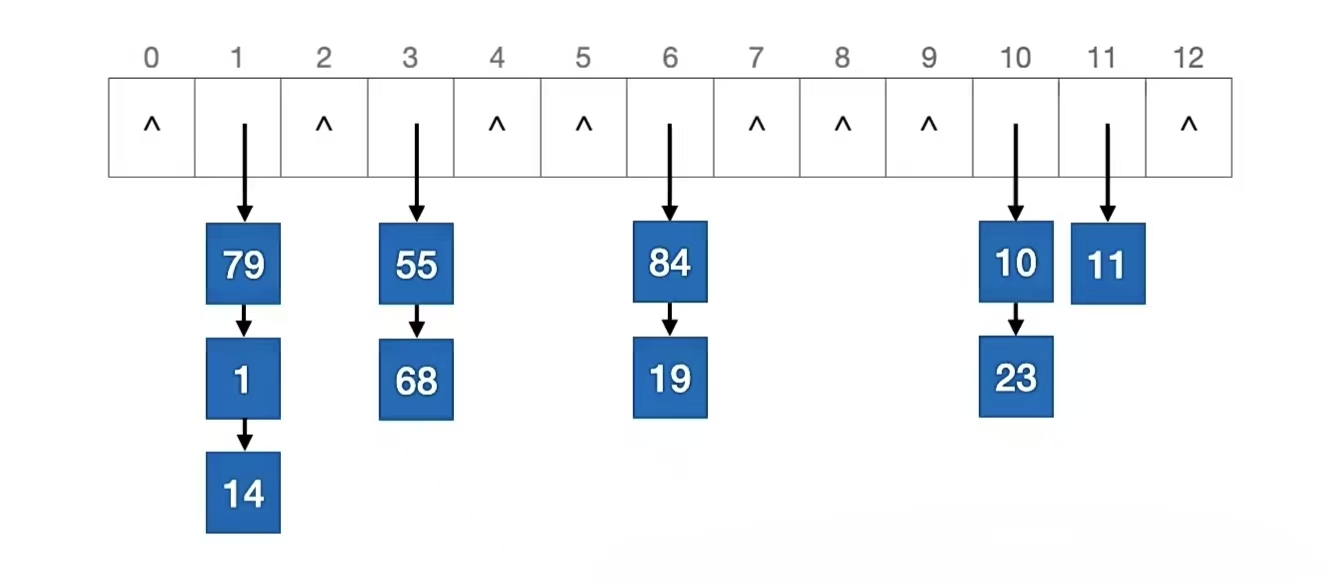
最后我们来删除“66”，删除首先要找到它才能删，找到它首先要计算目标元素存储地址：66 % 13 = 1，所以我们要在地址为“1”的地方从上往下捋，找到它再删除它

结果你猜怎么着？“66”查找失败了，所以我们没东西可以删，删除失败

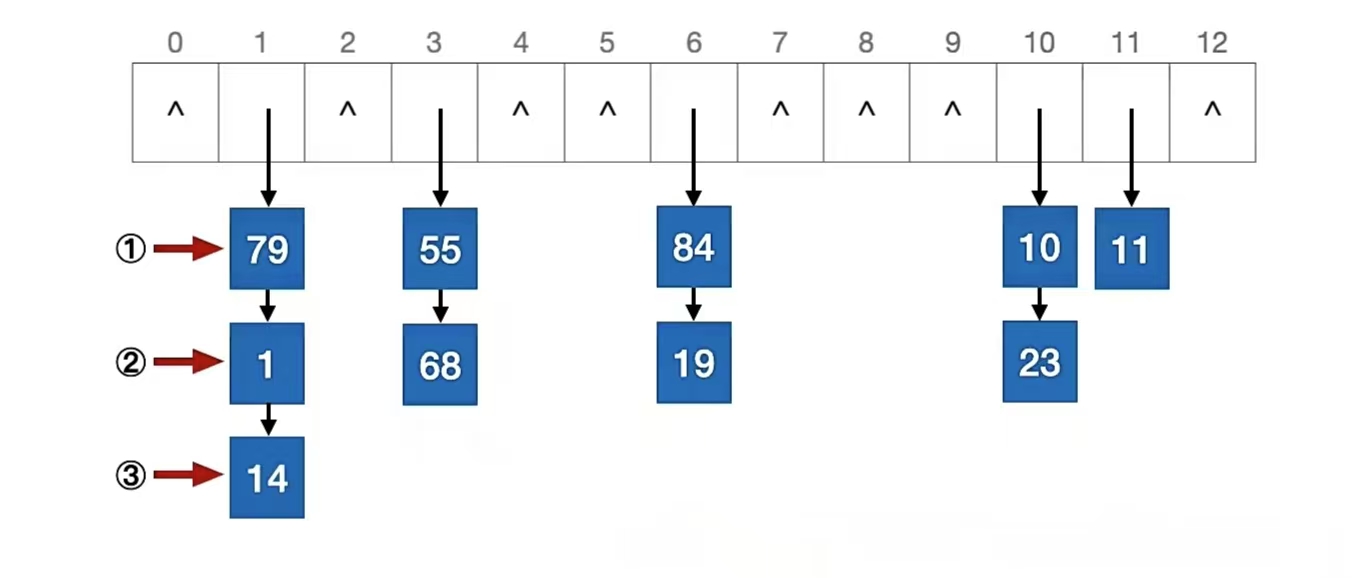
当然，如果想看得更直观，那么还是我们上上篇给出的地址可以直接看：

https://www.cs.usfca.edu/~galles/visualization/OpenHash.html

好东西~

我再多说一句，其实拉链法的插入操作有个小优化，也就是在新元素插入链表的时候，若能保持链表有序，则可以略微提高“查找”效率。

比如如果按照上述关键字，我们有序插入（升序）是这样的：

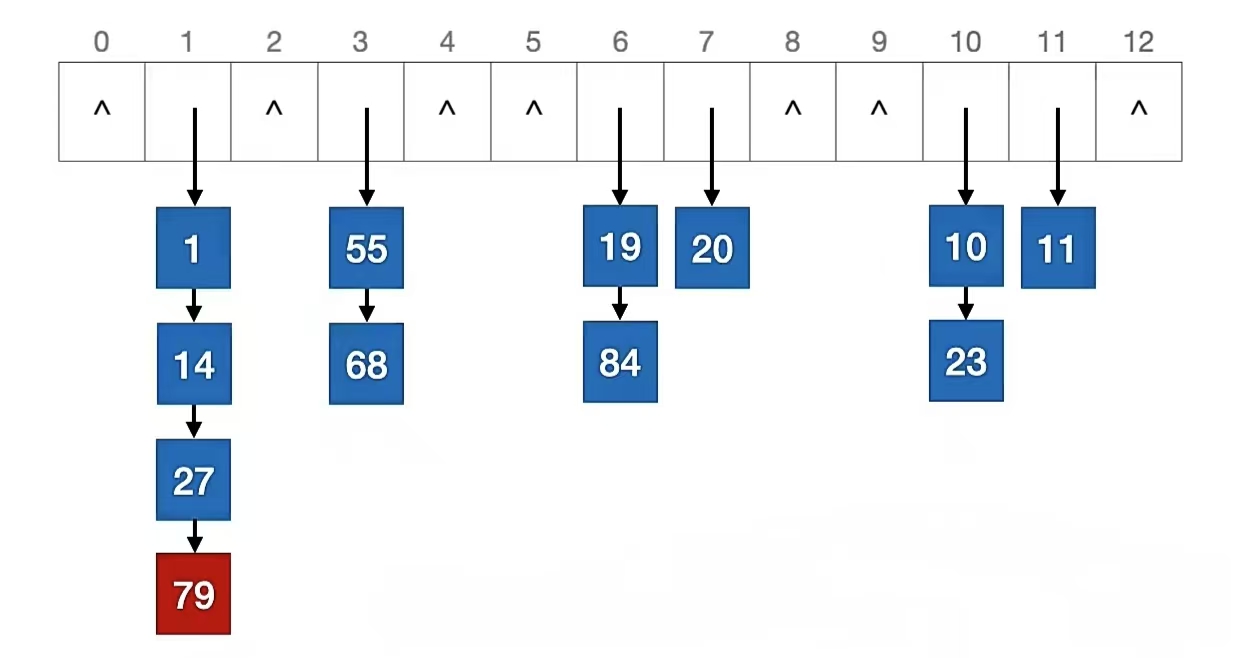
那么我们如果要查找关键字“16”，计算出“16”存放地址为 16 % 13 = 3，在地址为“3”的地方找，找到第一个“55”不是那就不用再往下找了，因为55>16，下面的肯定也比16大了，所以优化了查找长度。

2.开放定址法

我们有冲突，但是就不换散列函数，还有一种方式，那就是把没位置放的关键字放到其他空位置上，分成下面四个就是四种怎么找空位置的方法，其实本质就还是找位置。

开放定址法：如果发生“冲突”，就给新元素找另一个空闲位置，这个“另一个空闲位置”的找取也有不同的方法

这个“开放定址”，比较拗口，那么什么是“开放定址”？其实分成两个，一个是“开放”，一个是“定址”。“开放”是一个散列地址既对同义词开放，也对非同义词开放，也就是这个位置既可以放同义词，也可以放非同义词；“定址”就是确定地址，确定冲突了的那个去向何方。——沃兹基硕德

所以问题来了，我们怎么确定“另一个空闲位置”？它肯定是有一个“规则”的，可能是一个函数，可能是一个计算，但是不可能毫无规律乱放，不然放是放进去了，但是找就不好找了。

so我们需要确定一个“探测的顺序”， 从初始散列地址出发，去寻找下一个空闲位置，比如d₀=0，d₁=1，d₂=-1，d₃=2，d₄=2，……

注：d_i 表示第 i 次发生冲突时，下一个探测地址与初始散列地址的相对偏移量（探测序列/增量序列）。

有了这个相对偏移量，我们该怎么根据这个“偏移量”找到应该放的地址呢？

我们的散列函数为 H(key)，用它计算发现冲突，那么我们发生第 i 次冲突时的散列地址 H_i 就是 （初始散列地址 + 偏移量） % 散列表长度，即：

H_i = （ H(key) + d_i ）% m

我们就知道冲突的时候该放哪儿了，再也不用在外面漂荡了，完美。

其实我们还可以知道，无论是什么方法，d₀都是0（因为d_i 表示第 i 次发生冲突的偏移量，第 0 次发生冲突就是没有冲突，所以也就是直接 H(key) 就可以了。），还有就是其实我们最多也就可以处理 m - 1 次冲突的情况，即 0 ≤ i ≤ m-1，因为我们如果除了0全部都冲突，那么一直冲突一直放其他地方也会把散列表占满，所以下面的就没地方放了。

2.1 线性探测法

线性探测法： d_i = 0，1，2，3，……，m-1 （可以探测到散列表的每个地址）

发生冲突时 H_i = （ H(key) + d_i ）% m

我们用一个栗子来说明白这个东西，比如长度为13的散列表状态如下所示，散列函数 H(key) = key % 13，用 线性探测法 解决冲突。

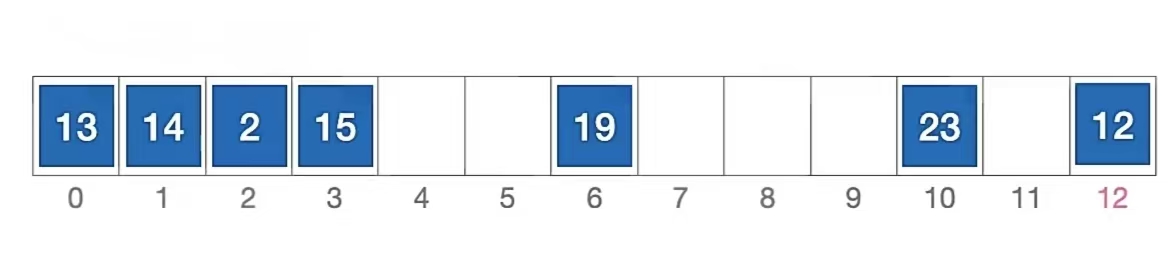
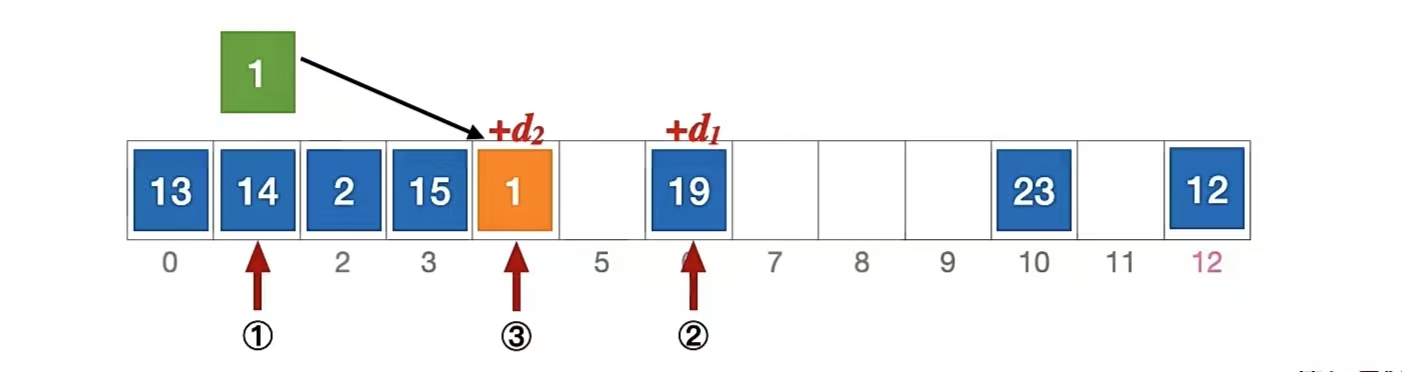
我们来分析一下插入元素 1 、查找元素 1 的过程，首先我们当然要算一下“1”应该插到哪里：

初始散列地址 H₀ = 1 % 13 = 1，发生冲突（第 1 次）（d₀ 是 0）
H₁ = （ 1 + 1 ） % 13 = 2 （d₁ 是 1），发生冲突（第 2 次）
H₂ = （ 1 + 2 ） % 13 = 3 （d₂ 是 2），发生冲突（第 3 次）
H₃ = （ 1 + 3 ） % 13 = 4 （d₃ 是 3），未发生冲突，插入位置 #4

所以“1”应该插入到下标为“4”的位置，即；

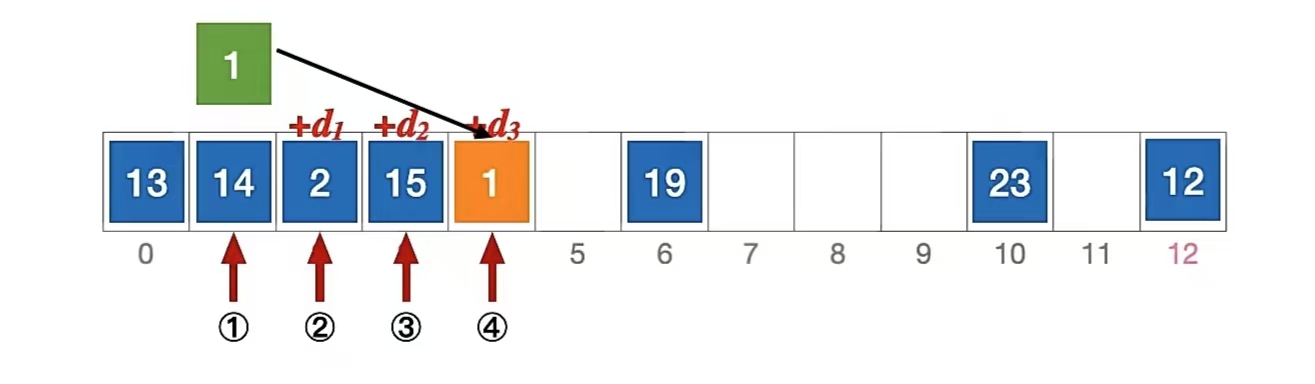
查找操作：根据探测序列依次对比个存储单元内的关键字
若探测到目标关键字，则查找成功；若探测到空单元，则查找失败

比如如果我们要找“27”，那么 H₀ = 27 % 13 = 1，所以我们应该找下标为“1”的地方，发现是“14”不是“27”，探测序列H₁应该是下一个，是“2”不是“27”，探测序列H₂是再下一个，是“15”不是“27”，探测序列H₃是再再下一个，还不是，是“1”不是“27”

此时！！！探测序列H₄是再再再下一个，我们发现它是空的，所以查找失败。（如果有“27”的话就放了，空的说明没有）.

2.2 平方探测法

平方探测法（又称二次探测法）： d_i = 0²，1²，-1²，2²，-2²，……，k²，-k²。（其中 k ≤ m/2）

发生冲突时 H_i = （ H(key) + d_i ）% m

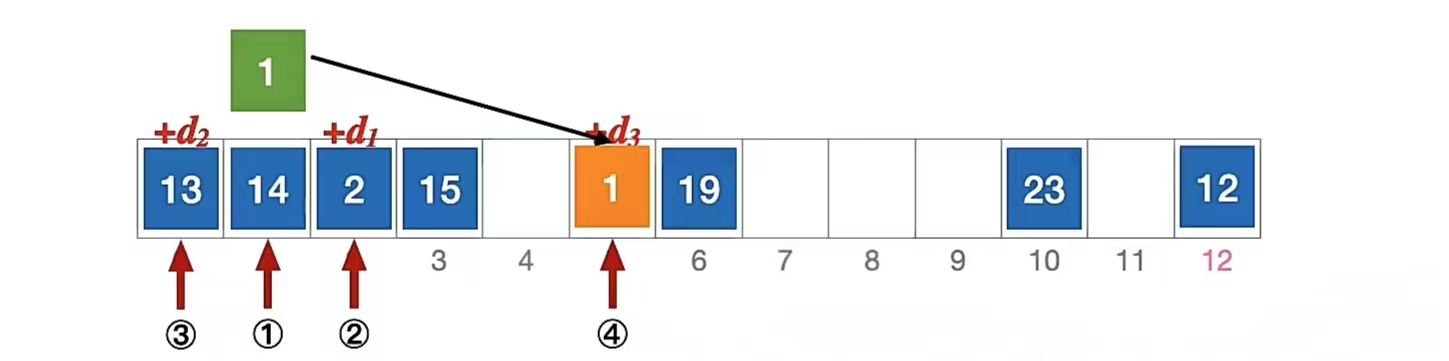
我们还用刚刚那个例子来说明，长度为13的散列表状态如下所示，散列函数 H(key) = key % 13，用 平方探测法 解决冲突：

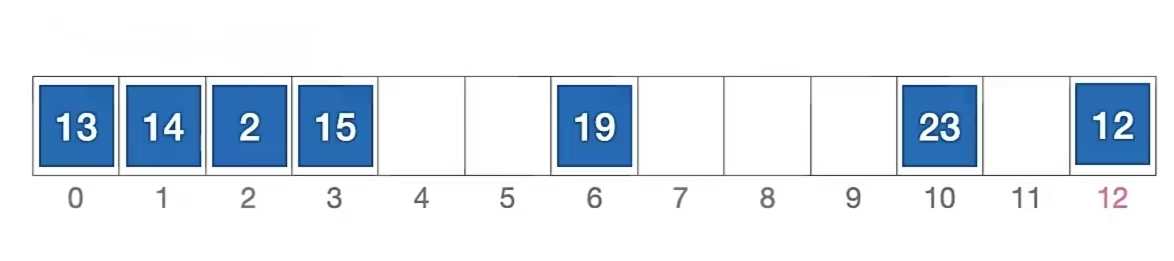
我们还是来分析一下插入元素 1 、查找元素 1 的过程，首先我们当然要算一下“1”应该插到哪里：

初始散列地址 H₀ = 1 % 13 = 1，发生冲突（第 1 次）（d₀ 是 0）
H₁ = （ 1 + 1 ） % 13 = 2 （d₁ 是 1），发生冲突（第 2 次）
H₂ = （ 1 + -1 ） % 13 = 0 （d₂ 是 -1），发生冲突（第 3 次）
H₃ = （ 1 + 4 ） % 13 = 5 （d₃ 是 4），未发生冲突，插入位置 #5

所以“1”应该插入到下标为“5”的位置，即；

查找也是一样，按照我们的探测序列一个一个找，直到找到就是成功，为空就是查找失败了，这里不再赘述。

2.3 双散列法

双散列法： d_i = i * hash₂（key）。其中 hash₂（key）是另一散列函数

发生冲突时 H_i = （ H(key) + d_i ）% m

我们又还是用刚刚那个例子来说明，长度为13的散列表状态如下所示，散列函数 H(key) = key % 13，用 双散列法 解决冲突，假设 hash₂（key） = 13 - （key%13）

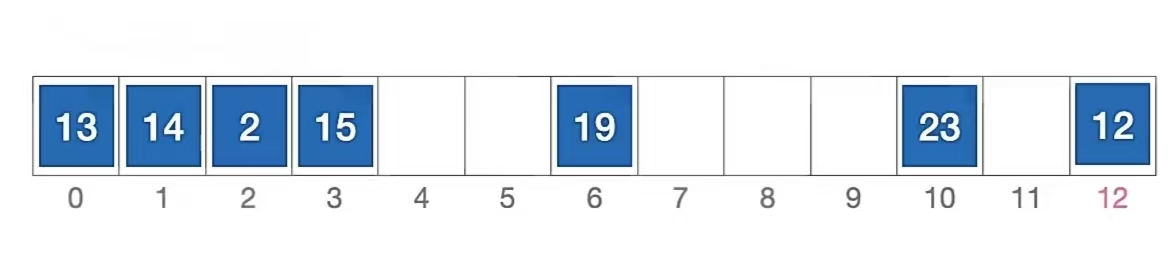
我们当然还是再来分析一下插入元素 1 、查找元素 1 的过程，首先我们当然还是要算一下“1”应该插到哪里：

双散列法： d_i = i * hash₂（key）

初始散列地址 H₀ = 1 % 13 = 1，发生冲突（第 1 次）（d₀ 是 0）
由于 key = 1， hash₂（key） = 13 - （key%13）= 12
H₁ = （ 1 + 1 * 12 ） % 13 = 0 （d₁ 是 1 * 12），发生冲突（第 2 次）
H₂ = （ 1 + 2 * 12 ） % 13 = 12 （d₂ 是 2 * 12 ），发生冲突（第 3 次）
H₃ = （ 1 + 3 * 12 ） % 13 = 11 （d₃ 是 3 * 12），未发生冲突，插入位置 #11

所以“1”应该插入到下标为“11”的位置，即；

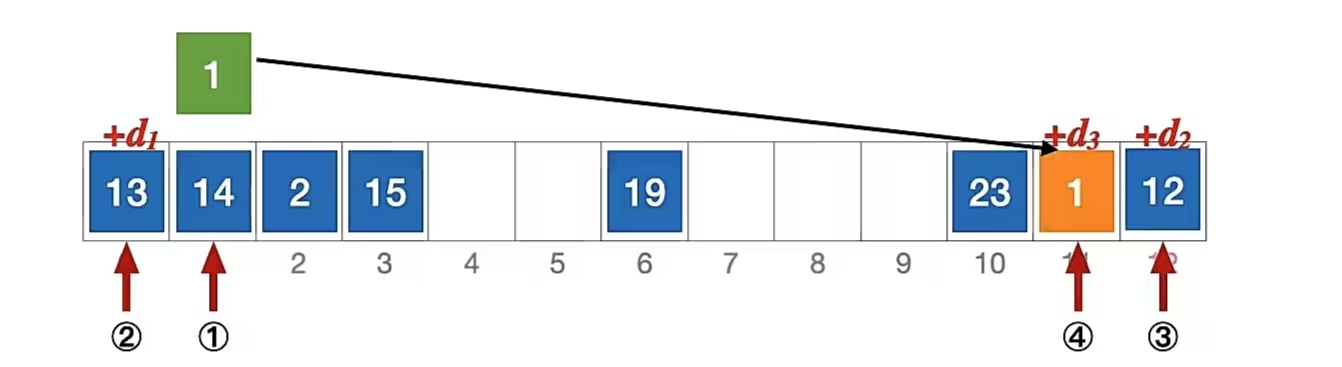
查找也是一样，按照我们的探测序列一个一个找，直到找到就是成功，为空就是查找失败了，这里不再赘述。

2.4 伪随机序列法

伪随机序列法 ：d_i是一个伪随机序列，如 d_i = 0，5，3，11，……

发生冲突时 H_i = （ H(key) + d_i ）% m

我们当然最后还是用刚刚那个例子来说明，长度为13的散列表状态如下所示，散列函数 H(key) = key % 13，用 伪随机序列法 解决冲突，假设伪随机序列 d_i = 0，5，3，11，……，其中 d_i 表示第 i 次发生冲突时的增量。

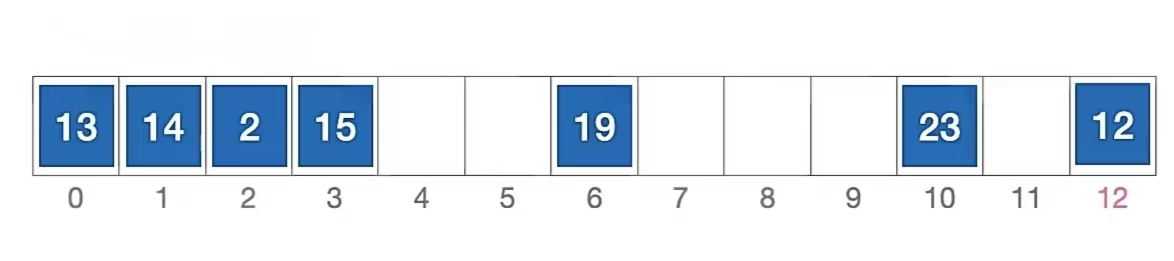
我们还是来分析一下插入元素 1 、查找元素 1 的过程，首先我们当然要算一下“1”应该插到哪里：

d_i 是一个伪随机序列，由题目可知 d_i = 0，5，3，11，……

初始散列地址 H₀ = 1 % 13 = 1，发生冲突（第 1 次）（d₀ 是 0）
H₁ = （ 1 + 5 ） % 13 = 6 （d₁ 是 5），发生冲突（第 2 次）
H₂ = （ 1 + 3 ） % 13 = 4 （d₂ 是 3），未发生冲突，插入位置 #4

所以“1”应该插入到下标为“4”的位置，即；

查找也是一样，按照我们的探测序列一个一个找，直到找到就是成功，为空就是查找失败了，这里不再赘述。

2.5 小结

小小总结一下，我们的四种常用方法构造探测序列（增量序列） d_i（注：0 ≤ i ≤ m-1）：

• ☆线性探测法 d_i = 0，1，2，3，……，m-1；

• 平方探测法 d_i = 0²，1²，-1²，2²，-2²，……，k²，-k²。（其中 k ≤ m/2）；

• 双散列法 d_i = i * hash₂（key）。其中 hash₂（key）是另一散列函数；

• 伪随机序列法 d_i是一个伪随机序列，如 d_i = 0，5，3，11，……

3.拓展

3.1 开放定址法的删除

如何删除一个元素？

1. 先根据散列函数算出散列地址，并对比关键字是否匹配，若匹配，则“查找成功”；
2. 若关键字不匹配，则根据“探测序列”对比下一个地址的关键字，直到“查找成功”或“查找失败”
3. 若“查找成功”，则删除找到的元素

注：题目一定会说明具体是采用哪种探测序列（线性探测法、平方探测法、双散列法、伪随机序列法）

看起来非常easy是吧，甚至不明白为什么还要单开一个说说是吧，马上就知道了。既然气氛都烘托到这了，还是那个例子：长度为13的散列表状态如下所示，散列函数 H(key) = key % 13，用 线性探测法 解决冲突：

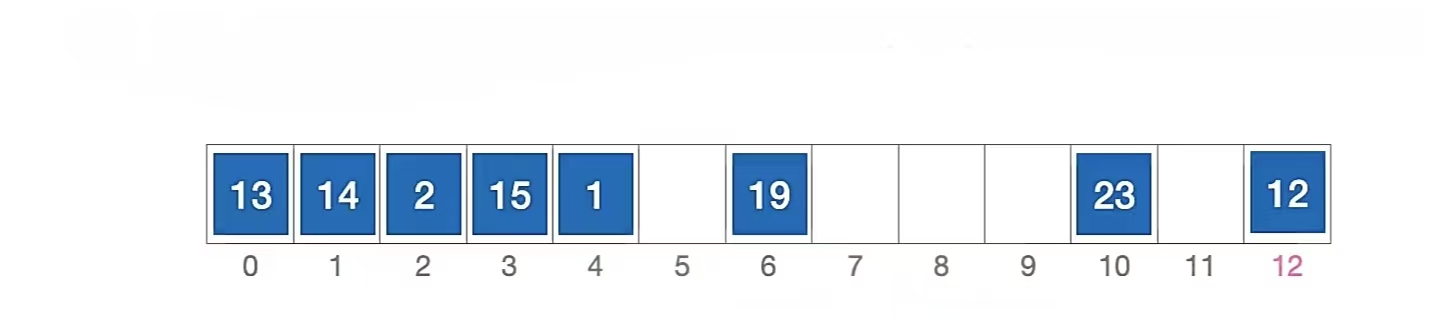
现在我们要删除元素“15”

• 计算元素“15”的初始散列地址 = 15 % 13 = 2，对比位置 #2，关键字不等于 15；
• 根据线性探测法的探测序列，继续对比位置 #3，关键字等于 15；
• 删除元素“15”，清空位置 #3

这非常正确，看起来没有任何毛病是吧，那我们再来查找元素“1”：

• 计算元素“1”的初始散列地址 = 1 % 13 = 1，对比位置 #1，关键字不等于 1；
• 根据线性探测法的探测序列，继续对比位置 #2，关键字不等于 1；
• 根据线性探测法的探测序列，继续对比位置 #3，探测到空单元，查找失败。

我们的查找过程：

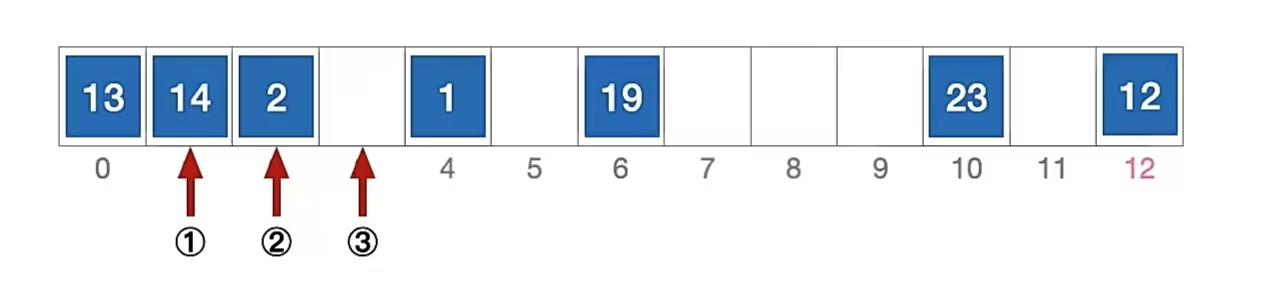
但是显然这是错的，因为我们是有“1”的，只是因为遇到空位置以为后面没了所以没查出来，这个“空位置”的存在是因为之前删掉给清空了，所以由此可知我们不可以那样删。

正确的做法：删除元素“15”：

• 计算元素“15”的初始散列地址 = 15 % 13 = 2，对比位置 #2，关键字不等于 15；
• 根据线性探测法的探测序列，继续对比位置 #3，关键字等于 15；
• 逻辑删除元素“15”，将位置 #3 标记为“已删除”（比如设个flag=1什么的）

注意：采用“开放定址法”时，删除元素不能简单地将被删元素的空间置为空，否则将截断在它之后的探测路径，可以做一个“已删除”标记，进行逻辑删除。

无论是线性探测法、平方探测法、双散列法、伪随机序列法原理都一样，删除元素时，只能逻辑删除。

正确示例：查找元素“1”：

• 计算元素“1”的初始散列地址 = 1 % 13 = 1，对比位置 #1，关键字不等于 1；
• 根据线性探测法的探测序列，继续对比位置 #2，关键字不等于 1；
• 根据线性探测法的探测序列，继续对比位置 #3，该位置原关键字已删，继续探测后一个位置；
• 根据线性探测法的探测序列，继续对比位置 #4，关键字等于1，查找成功；。

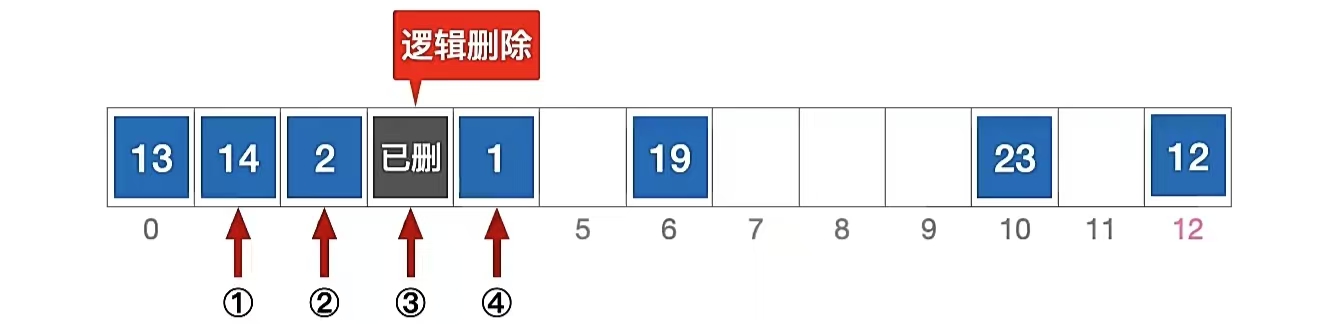
但是！！！！这样也会有问题，想不到吧。啥问题？就是查找效率会比较低，因为这样的话，我们删掉一个做一个标记，但是里面还是有元素，所以散列表看起来很满，实则很空。

那我们该怎么办呢？其实很容易想，满了怎么办，清理一下就好了，所以我们可以不定期整理散列表内的数据。

还有就是我们虽然是逻辑假删除，但是我们在插入数据的时候就别管它是真删假删了，就通通当做真删除就可以了，所以新元素也可以插入到已被“逻辑删除”的地址。

3.2 探测覆盖率

线性探测法

我们“线性探测法”一直冲突如下所示：

采用“线性探测法”，一定可以探测到散列表的每个位置，只要散列表中有空闲位置，就一定可以插入成功。

因为它是一个接着下一个开始找的，如果有空闲位置，那么一个一个遍历迟早高低能遍历到，只是时间的早晚问题而已。

理想情况下，若散列表表长=m，则最多发生m-1次冲突即可“探测”完整个散列表。

平方探测法

我们“平方探测法”一直冲突如下所示：

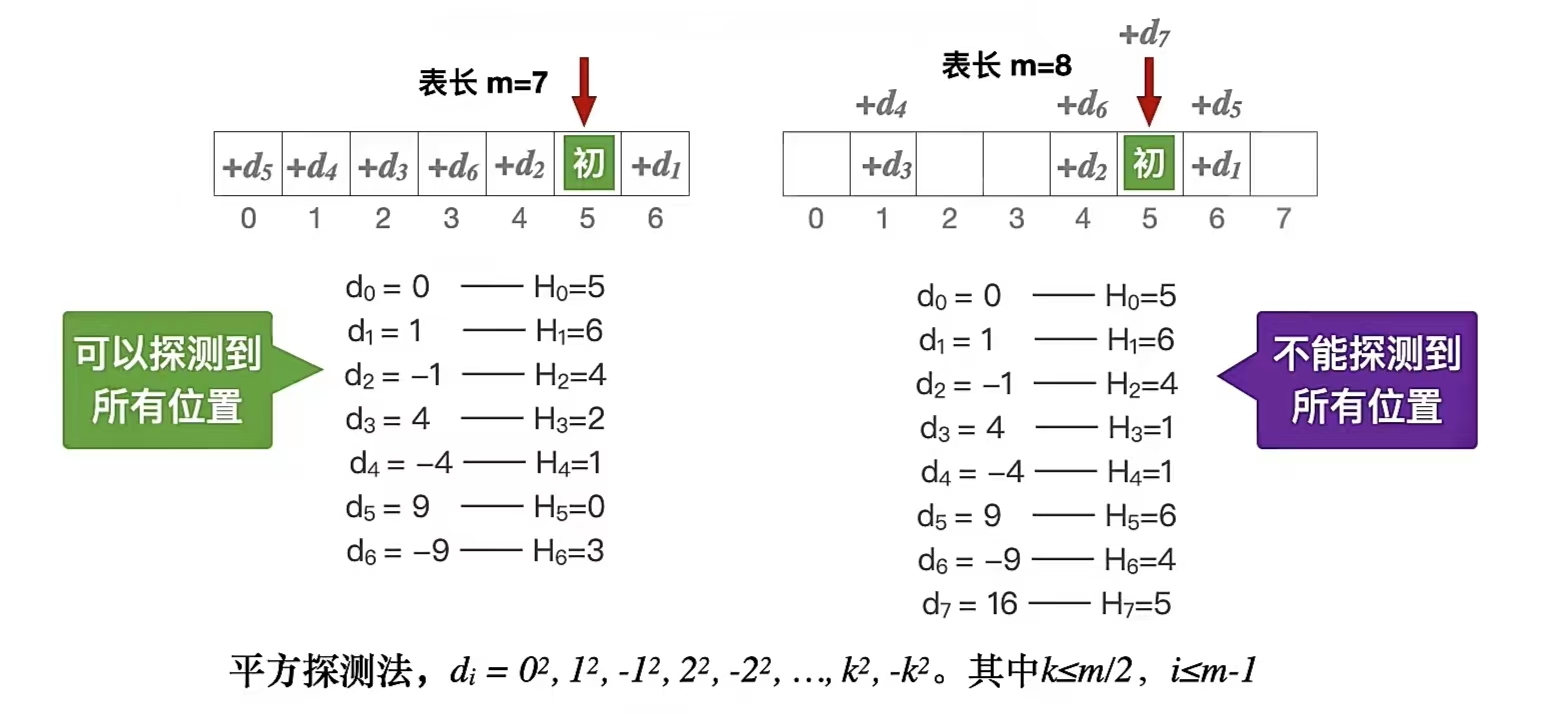
采用“平方探测法”，至少可以探测到散列表中一半的位置。这意味着，即便散列表中有空闲位置，也未必能插入成功。

由上图可知，表长为7就能探测完所有位置，表长为8就不能，所以能不能“探测”完整个散列表和散列表的长度有关系。

当然，这个我们也是有结论的：若散列表长度 m 是一个可以表示成 4 * j + 3 的素数如（7、11、19），平方探测法就能探测到所有位置。为啥？还是要追溯到《数论》。还是那句话，计算机的尽头是数学，所以要想做计算机研究少不了得数学好才行。

双散列法

我们“双散列法”一直冲突如下所示：

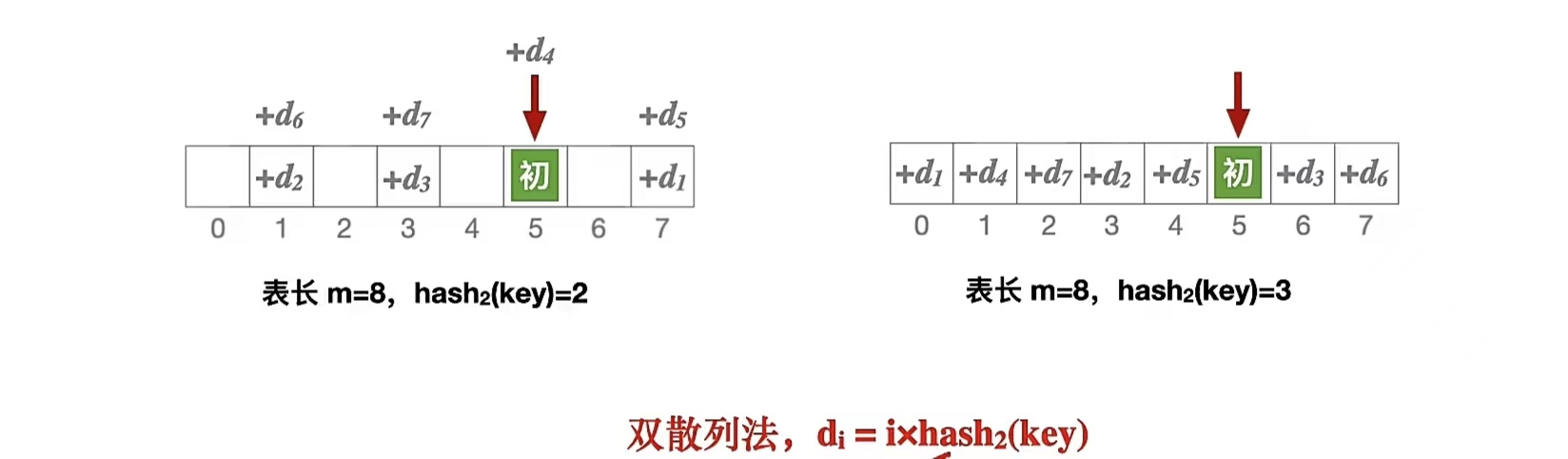
双散列法未必能探测到散列表的所有位置。

由上图可知，双散列表法的探测覆盖率取决于第二个散列函数 hash₂(key) 设计的是否合理

若 hash₂(key) 计算得到的值与散列表表长 m 互质，就能保证双散列法可以探测所有单元，这个也是数学原因，知道这么个意思就行了。

双散列法常用套路：令表长 m 本身就是质数，hash₂(key) = m - (key % m)，则无论 key 值是多少，hash₂(key) 和 m 一定互质。

伪随机序列法

我们“伪随机序列法”一直冲突如下所示：

伪随机序列法：d_i 是一个伪随机序列，由程序员人为设计

这就是随机的了，能不能探测完整个散列表全靠命。

采用伪随机序列法，是否能探测到散列表中全部位置，取决于伪随机序列的设计是否合理

总结

我们说了什么是散列表，什么是散列函数，有冲突后我们可以换散列函数/不换散列函数，换散列函数就是四个，有除留余数法，也就是让散列函数等于key模p，p是不大于散列表长的质数；还有直接定址法，就跟一个直线方程一样，散列函数直接等于a * key+b这样。还有个数字分析法，去手机号后四位那个。最后剩个平方取中法，给它平方再取中间几位。不换散列函数就是看冲突了怎么办，一个是直接链接起来，也就是拉链法，还有一个是找其他位置，也就是开放定址法。

开放定址法有四个，线性探测是增量序列是0,1,2,3……这样往上增，平方探测法是增量序列是0,1,-1,2,-1……这样，双散列法是再来个散列函数，d_几就是几*冲突的位置代入到第二个散列函数得到的值，伪随机序列法就是增量序列是随机给个序列，冲突后我们第几次找新地址的值就是原来冲突的地址+d_几再代入到原散列函数中就可以了。