从“一步到位”到“平滑过渡”:深入浅出最少拍与大林控制算法
在自动化控制的世界里,我们的终极目标通常很朴素:让一个系统(比如房间的温度、汽车的速度、机械臂的位置)听我们的话,精确地达到我们设定的目标值。PID 控制器是这个领域的常青树,它简单、有效,几乎无处不在。
但是,当我们的控制器从模拟电路变成了计算机程序,进入了“数字控制”的时代,我们就有了更广阔的的想象空间。计算机按照固定的节拍(采样周期)工作,这让我们能设计出一些在模拟世界里难以想象的精妙算法。
今天,我们就来聊聊两种非常有代表性的数字控制算法:最少拍控制(Deadbeat Control) 和 大林算法(Dahlin’s Algorithm)。
它们的设计思想非常巧妙,一个追求极致的“快”,力求在最短的时间内“一步到位”;另一个则在“快”的基础上,增加了“稳”的考量,追求“平滑过渡”。理解了它们,你对数字控制的理解会迈上一个全新的台阶。
一、故事的起点:数字控制的世界观
在深入算法之前,我们必须先统一“世界观”。想象一下,你正在玩一个像素风格的老游戏,你控制的角色只能在屏幕上的一个个格子里跳动,而不能像现实世界一样平滑地移动。
数字控制系统眼中的世界,就是这样的“像素格子”世界。它不像模拟控制器那样持续不断地观察和调整,而是每隔一个固定的时间(称为采样周期 T),看一眼系统的当前状态,然后计算一下接下来该做什么。
- 采样(Sampling):每隔 T 秒,用传感器测量一次系统状态(如温度、速度),把连续变化的物理量变成一个离散的数字。
- 计算(Computation):控制器(你的电脑或单片机)根据这个数字,和你的设定目标,运行控制算法,得出一个控制指令(如加热器的功率、电机的电压)。
- 保持(Holding):这个控制指令会一直保持不变,直到下一个采样周期到来,控制器才会根据新的测量值计算出新的指令。这个过程通常由“零阶保持器”完成。
这个“采样-计算-保持”的循环,就是数字控制的核心。
认识数字世界的“语言”:Z变换
在模拟控制中,我们用拉普拉斯变换(s域)来分析系统。到了数字控制,我们有了一个新工具:Z变换。
别怕,我们不深入复杂的数学推导。你只需要记住一个核心思想:Z变换是数字世界的“语言”,它有一个神奇的“时光机”操作符: z − 1 z^{-1} z−1。
z − 1 z^{-1} z−1 的含义是:将一个信号延迟一个采样周期 T。
举个例子,假设 u ( k ) u(k) u(k) 是我们在“当前”这个时间点(第k个采样周期)计算出的控制指令。
那么:
- z − 1 u ( k ) z^{-1}u(k) z−1u(k) 就代表上一个时间点(第k-1个采样周期)的控制指令 u ( k − 1 ) u(k-1) u(k−1)。
- z − 2 u ( k ) z^{-2}u(k) z−2u(k) 就代表上上个时间点(第k-2个采样周期)的控制指令 u ( k − 2 ) u(k-2) u(k−2)。
是不是很简单? z − 1 z^{-1} z−1 就是一个“回溯”一拍的指令。有了这个工具,我们就可以把描述系统动态的微分方程,转换成只包含加减乘除和延迟的代数方程(称为差分方程),计算机处理起来就得心应手了。
一个被控对象(比如一个加热炉),在模拟世界里我们用传递函数 G ( s ) G(s) G(s) 来描述它。经过“采样”和“零阶保持器”的数字化处理后,它在数字世界里的等效模型就变成了脉冲传递函数 G ( z ) G(z) G(z)。
我们的任务,就是设计一个数字控制器 D ( z ) D(z) D(z),去控制这个 G ( z ) G(z) G(z)。
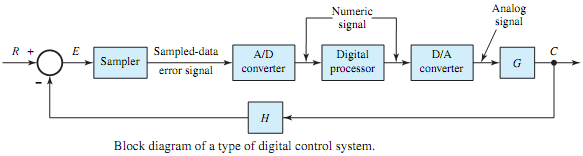
上图是一个典型的数字控制系统闭环框图。
- R ( z ) R(z) R(z) 是我们给定的目标值(Setpoint),比如我们希望温度达到80度。
- Y ( z ) Y(z) Y(z) 是系统的实际输出值(Output),比如当前炉子的实际温度。
- E ( z ) E(z) E(z) 是误差,即 E ( z ) = R ( z ) − Y ( z ) E(z) = R(z) - Y(z) E(z)=R(z)−Y(z)。
- D ( z ) D(z) D(z) 是我们设计的数字控制器,它的输入是误差 E ( z ) E(z) E(z),输出是控制量 U ( z ) U(z) U(z)。
- G ( z ) G(z) G(z) 是被控对象的脉冲传递函数。
根据这个图,我们可以推导出整个闭环系统的传递函数 Φ ( z ) \Phi(z) Φ(z):
Φ ( z ) = Y ( z ) R ( z ) = D ( z ) G ( z ) 1 + D ( z ) G ( z ) \Phi(z) = \frac{Y(z)}{R(z)} = \frac{D(z)G(z)}{1 + D(z)G(z)} Φ(z)=R(z)Y(z)=1+D(z)G(z)D(z)G(z)
这个公式是所有设计的核心!我们的目标就是:通过精心设计 D ( z ) D(z) D(z),让我们想要的闭环响应 Φ ( z ) \Phi(z) Φ(z) 得以实现。
换句话说,我们不再像PID那样“盲调”参数,而是先“定义”一个我们心目中最完美的系统响应 Φ d e s ( z ) \Phi_{des}(z) Φdes(z)(des for desired),然后反推出控制器 D ( z ) D(z) D(z) 应该长什么样。
从上面的公式,我们可以反解出 D ( z ) D(z) D(z):
D ( z ) = Φ d e s ( z ) G ( z ) ( 1 − Φ d e s ( z ) ) D(z) = \frac{\Phi_{des}(z)}{G(z)(1 - \Phi_{des}(z))} D(z)=G(z)(1−Φdes(z))Φdes(z)
这个公式就是我们设计算法的“万能钥匙”。接下来,最少拍和大林算法的区别,就在于它们对“最完美的响应” Φ d e s ( z ) \Phi_{des}(z) Φdes(z) 有着不同的定义。
二、最少拍控制:追求极致速度的“急性子”
最少拍控制(Deadbeat Control),从名字就能听出它的性格:干脆利落,不拖泥带水。它的设计目标是:在设定值 R ( z ) R(z) R(z) 发生阶跃变化(比如温度从20度突然要求升到80度)后,系统的输出 Y ( z ) Y(z) Y(z) 要在最少的采样周期数内,精确地达到并稳定在新的设定值上,且后续没有任何误差。
“最少”是多少?这取决于被控对象 G ( z ) G(z) G(z) 的“先天延迟”。
一个实际的物理系统,从你给它一个指令到它开始有响应,总会有一个纯粹的延迟时间。在 G ( z ) G(z) G(z) 模型中,这通常表现为 z − d z^{-d} z−d 的形式,其中 d 代表延迟了 d 个采样周期。
既然系统先天就要延迟 d 拍,那我们能期待的最快响应,就是在第 d 拍结束后,输出就能一步到位。
最少拍的设计哲学
最少拍算法说:“我想要的完美响应 Φ d e s ( z ) \Phi_{des}(z) Φdes(z) 就是纯延迟!”
Φ d e s ( z ) = z − d \Phi_{des}(z) = z^{-d} Φdes(z)=z−d
这个公式是什么意思?我们来看一下。我们希望 Y ( z ) = Φ d e s ( z ) R ( z ) Y(z) = \Phi_{des}(z) R(z) Y(z)=Φdes(z)R(z)。
如果输入是一个阶跃信号(在数字世界里,它的Z变换是 R ( z ) = 1 1 − z − 1 R(z) = \frac{1}{1-z^{-1}} R(z)=1−z−11),那么输出就是:
Y ( z ) = z − d 1 1 − z − 1 Y(z) = z^{-d} \frac{1}{1-z^{-1}} Y(z)=z−d1−z−11。
这个 Y ( z ) Y(z) Y(z) 对应的时域序列,在第 0, 1, …, d-1 拍时,输出都是0。在第 d, d+1, d+2, … 拍开始,输出就恒定为1了。这意味着,系统在 d 拍的延迟后,瞬间就达到了目标值,并且稳稳地保持住,没有任何超调和振荡。
这简直是控制领域的“完美梦想”!
推导最少拍控制器
现在,我们将这个“完美梦想”代入我们的“万能钥匙”公式:
D ( z ) = Φ d e s ( z ) G ( z ) ( 1 − Φ d e s ( z ) ) = z − d G ( z ) ( 1 − z − d ) D(z) = \frac{\Phi_{des}(z)}{G(z)(1 - \Phi_{des}(z))} = \frac{z^{-d}}{G(z)(1 - z^{-d})} D(z)=G(z)(1−Φdes(z))Φdes(z)=G(z)(1−z−d)z−d
我们通常会将对象的传递函数 G ( z ) G(z) G(z) 分解成两部分:
G ( z ) = G 0 ( z ) ⋅ z − d G(z) = G_0(z) \cdot z^{-d} G(z)=G0(z)⋅z−d
其中 z − d z^{-d} z−d 是系统的纯延迟部分,而 G 0 ( z ) G_0(z) G0(z) 是不包含延迟的“主体”部分。代入上式,得到:
D ( z ) = z − d G 0 ( z ) z − d ( 1 − z − d ) = 1 G 0 ( z ) ( 1 − z − d ) D(z) = \frac{z^{-d}}{G_0(z)z^{-d}(1 - z^{-d})} = \frac{1}{G_0(z)(1 - z^{-d})} D(z)=G0(z)z−d(1−z−d)z−d=G0(z)(1−z−d)1
这就是最少拍控制器的最终形式。只要我们知道了被控对象的模型 G ( z ) G(z) G(z)(也就是知道了 G 0 ( z ) G_0(z) G0(z) 和 d),我们就能直接写出控制器的表达式。
最少拍的“魔鬼细节”:优点与陷阱
最少拍算法看起来如此完美,为什么在实际工业中却不常用呢?因为它是一个典型的“理论上的巨人,实践中的病人”。
优点:
- 响应神速:在模型完全精确的理想情况下,它能实现理论上最快的无误差跟踪。
- 设计简单:一旦有了对象模型,控制器设计就是一道代数题,无需像PID那样反复调试。
致命缺陷:
对模型精度要求极高:它是基于模型的控制。如果你的 G ( z ) G(z) G(z) 模型有任何一点偏差(哪怕是细微的参数错误),实际效果就会大打折扣,甚至导致系统不稳定。现实中,完美的模型几乎不存在。
控制量可能过大(“猛踩油门”):为了让输出“一步到位”,控制器可能会在第一个采样周期就计算出一个非常巨大的控制量(比如瞬间把加热器开到200%的功率)。这在物理上往往是不可行的,甚至会损坏设备。
稳态零点问题(ZOHO, Zero-Order Hold Pole/Zero Cancellation):这是最隐蔽也最危险的问题。在推导 G ( z ) G(z) G(z) 的过程中,通常会引入一些不稳定的零点(位于Z平面单位圆外的零点)。最少拍控制器在设计时,会试图“抵消”掉 G ( z ) G(z) G(z) 的所有零极点。如果它试图抵消一个不稳定的零点,会导致控制器本身变得不稳定,从而在两个采样点之间产生剧烈的振荡,这种现象称为采样间纹波(Intersample Ripple)。
想象一下,你在像素格子上看,角色每一步都精准地落在目标格子上。但如果你能看到格子之间的“慢动作”,你会发现角色在空中疯狂地抽搐和翻滚,只是恰好在每一拍结束时,它的脚能踩在格子上。这种“疯狂抽搐”对于执行机构(如电机、阀门)是巨大的折磨。
正是因为这些苛刻的条件和潜在的风险,最少拍算法更像是一个理论上的“标杆”,它告诉我们数字控制能达到的极限速度是什么样的。在实践中,我们需要一个更稳重、更宽容的伙伴。
三、大林算法:追求平滑过渡的“稳重派”
如果说最少拍是一个追求极致速度、不计代价的“天才少年”,那么大林算法(Dahlin’s Algorithm)就是一位经验丰富、懂得权衡利弊的“成熟工程师”。
大林算法的设计者 E. B. Dahlin 认识到,在现实世界中,“一步到位”的完美响应不仅难以实现,而且往往没有必要,甚至是有害的。用户通常更关心系统是否能平稳、无超调地达到目标,哪怕稍微慢一点点。
大林算法的设计哲学
大林算法修改了那个“完美梦想”。它说:“我想要的响应,不是瞬间跳变,而是一个像现实世界中一阶惯性系统那样的、平滑的指数级靠近。”
在模拟世界里,一阶系统的响应是 e − t / λ e^{-t/\lambda} e−t/λ 的形式,其中 λ \lambda λ 是时间常数,控制着响应的快慢。大林算法就把这个思想搬到了数字世界。
它定义了这样一个理想的闭环响应:
Φ d e s ( z ) = ( 1 − a ) z − ( d + 1 ) 1 − a z − 1 \Phi_{des}(z) = \frac{(1-a)z^{-(d+1)}}{1-az^{-1}} Φdes(z)=1−az−1(1−a)z−(d+1)
这个公式看起来有点复杂,我们来拆解一下:
分母 1 − a z − 1 1-az^{-1} 1−az−1:这是核心!它在数字世界里模拟了一个一阶惯性环节。 a a a 是一个可调参数,它的值介于0和1之间,由 a = e − T / λ a = e^{-T/\lambda} a=e−T/λ 决定。
- λ \lambda λ 就是我们期望的闭环响应时间常数。 λ \lambda λ 越大,a 越接近1,系统响应越慢、越平滑。 λ \lambda λ 越小,a 越接近0,系统响应越快、越激进。
- 当 λ → 0 \lambda \to 0 λ→0 时, a → 0 a \to 0 a→0,分母变成1,大林算法就无限趋近于最少拍算法了!所以, λ \lambda λ 是我们调节系统“快”与“稳”的唯一旋钮。
分子 ( 1 − a ) z − ( d + 1 ) (1-a)z^{-(d+1)} (1−a)z−(d+1):这一部分有两个作用。
- z − ( d + 1 ) z^{-(d+1)} z−(d+1):这里为什么是 d+1?因为大林算法的响应形式是指数曲线,它不像最少拍那样可以“瞬间完成”,它需要至少一个计算周期来启动这个指数过程。所以总延迟是 d(系统固有延迟)+ 1(算法计算延迟)。
- ( 1 − a ) (1-a) (1−a):这是一个增益校正项。它的作用是保证当时间趋于无穷时,系统的稳态增益为1。也就是说,只要你等得足够久,输出 Y ( z ) Y(z) Y(z) 一定能精确地等于输入 R ( z ) R(z) R(z),没有稳态误差。
推导大林控制器
同样,我们将大林定义的 Φ d e s ( z ) \Phi_{des}(z) Φdes(z) 代入“万能钥匙”公式:
D ( z ) = Φ d e s ( z ) G ( z ) ( 1 − Φ d e s ( z ) ) D(z) = \frac{\Phi_{des}(z)}{G(z)(1 - \Phi_{des}(z))} D(z)=G(z)(1−Φdes(z))Φdes(z)
代入并化简后,可以得到大林控制器的表达式。我们还是把 G ( z ) G(z) G(z) 写成 G 0 ( z ) z − d G_0(z)z^{-d} G0(z)z−d 的形式:
D ( z ) = ( 1 − a ) z − ( d + 1 ) 1 − a z − 1 G 0 ( z ) z − d ( 1 − ( 1 − a ) z − ( d + 1 ) 1 − a z − 1 ) D(z) = \frac{\frac{(1-a)z^{-(d+1)}}{1-az^{-1}}}{G_0(z)z^{-d}(1 - \frac{(1-a)z^{-(d+1)}}{1-az^{-1}})} D(z)=G0(z)z−d(1−1−az−1(1−a)z−(d+1))1−az−1(1−a)z−(d+1)
经过一番化简(分子分母同乘以 ( 1 − a z − 1 ) (1-az^{-1}) (1−az−1)),最终得到:
D ( z ) = ( 1 − a ) z − 1 G 0 ( z ) ( 1 − a z − 1 − ( 1 − a ) z − ( d + 1 ) ) D(z) = \frac{(1-a)z^{-1}}{G_0(z)(1 - az^{-1} - (1-a)z^{-(d+1)})} D(z)=G0(z)(1−az−1−(1−a)z−(d+1))(1−a)z−1
这个公式看起来比最少拍的复杂,但它的内涵却更加丰富和实用。
大林的智慧:如何解决最少拍的陷阱
大林算法通过引入可调参数 λ \lambda λ (或 a),巧妙地规避了最少拍的几大问题:
降低对模型精度的敏感度:当你选择一个较大的 λ \lambda λ 时,系统响应变缓,控制作用也变得温和。这种“温和”的策略对模型的小误差有更强的容忍度(鲁棒性)。就像开车,你开得慢一点,即使路况稍微有些预期之外的变化,你也来得及调整。
避免过大的控制量:由于响应曲线是平滑的,控制器计算出的控制量也不会像最少拍那样极端,避免了“猛踩油门”和“猛踩刹车”的情况,保护了物理设备。
处理采样间纹波:大林算法在设计时,同样会面临“坏”零点(不稳定零点和振荡性强的零点)的抵消问题。一个改进版的大林算法会这样做:在计算 G 0 ( z ) G_0(z) G0(z) 的逆时,并不会把 G 0 ( z ) G_0(z) G0(z) 的所有零点都抵消掉,而是有选择性地保留那些“坏”的零点。这样虽然会牺牲一点点跟踪速度,但能有效抑制采样间纹波,保证控制过程的平顺。这是一种非常工程化的智慧——有舍才有得。
最少拍 vs. 大林:总结与抉择
| 特性 | 最少拍控制器 (Deadbeat) | 大林控制器 (Dahlin) |
|---|---|---|
| 设计目标 | 最短时间无差跟踪 | 平滑、无超调、一阶响应 |
| 响应速度 | 理论最快 | 可调,通常比最少拍慢 |
| 调节参数 | 无 | 闭环时间常数 λ \lambda λ |
| 控制作用 | 可能非常剧烈 | 相对平缓温和 |
| 模型依赖性 | 极高,非常敏感 | 较高,但对误差有一定容忍度 |
| 稳定性问题 | 容易出现采样间纹波 | 通过保留“坏”零点可有效抑制 |
| 适用场景 | 理论研究,对速度要求极致且模型精确的场合 | 绝大多数工业过程控制,特别是希望平稳、无超调的场合 |
你该如何选择?
- 如果你的系统模型非常精确,并且你追求的是绝对的响应速度,不惜一切代价(比如某些高速定位系统),那么最少拍算法是你的理论上限参考。
- 在几乎所有其他的工业应用中,尤其是化工、热工等过程控制领域,大林算法及其变种都是更优越、更实用的选择。它提供了一个关键的调节旋钮 λ \lambda λ,让工程师可以在“速度”和“平稳性”之间找到最佳的平衡点,这正是工程实践的精髓所在。
结语
从追求“一步到位”的最少拍,到懂得“平滑过渡”的大林,我们看到的是控制算法设计思想的演进。这不仅仅是数学公式的变化,更是从理想化的理论模型走向复杂的工程现实的必然一步。
最少拍算法像一位剑客,追求一击必杀,对剑(模型)和环境(工况)的要求都极为苛刻。而大林算法则更像一位太极宗师,招式圆融,后发制人,讲究的是用最小的力气,达到最稳定、和谐的状态。
掌握了这两种算法,你不仅学会了两种具体的控制器设计方法,更重要的是,你理解了一种核心的设计范式——基于模型的预测控制思想。先定义出你期望的系统行为,然后反推出能实现这一行为的控制器。这是通往更高级控制算法(如模型预测控制MPC)的必经之路。
希望这篇博文能为你打开数字控制世界的一扇新窗。
习题
为了巩固今天学习的知识,这里有几道练习题。
背景:假设我们有一个简单的加热系统,其传递函数模型为:
G ( s ) = e − 2 s 5 s + 1 G(s) = \frac{e^{-2s}}{5s+1} G(s)=5s+1e−2s
我们选择采样周期 T = 1 T=1 T=1 秒。经过Z变换后,其脉冲传递函数为:
G ( z ) = 0.1813 z − 3 1 − 0.8187 z − 1 G(z) = \frac{0.1813 z^{-3}}{1 - 0.8187 z^{-1}} G(z)=1−0.8187z−10.1813z−3
(提示:这是一个带二阶延迟的一阶系统,总延迟 d = 2 + 1 = 3 d=2+1=3 d=2+1=3个采样周期,但为简化计算,我们直接使用给出的 G ( z ) G(z) G(z) 模型,其纯延迟为 d = 3 d=3 d=3)。
问题1:最少拍控制器设计
根据给定的 G ( z ) G(z) G(z),设计一个最少拍控制器 D ( z ) D(z) D(z)。写出 D ( z ) D(z) D(z) 的表达式。
问题2:大林控制器设计
同样针对这个 G ( z ) G(z) G(z),设计一个大林控制器。我们期望闭环响应时间常数 λ = 4 \lambda = 4 λ=4 秒。请计算出调节参数 a a a,并写出大林控制器 D ( z ) D(z) D(z) 的表达式。
问题3:概念思考
如果在使用问题1中设计的最少拍控制器时,发现执行器(加热器)在开关时动作过于剧烈,几乎是在满功率和零功率之间反复横跳,但采样点上的温度值却很完美。这最可能是什么现象?你会考虑切换到大林控制器吗?为什么?
答案
答案1:
对于最少拍控制器,我们希望闭环响应为 Φ d e s ( z ) = z − d = z − 3 \Phi_{des}(z) = z^{-d} = z^{-3} Φdes(z)=z−d=z−3。
首先,从 G ( z ) G(z) G(z) 中分离出延迟部分和非延迟部分:
G ( z ) = 0.1813 1 − 0.8187 z − 1 ⏟ G 0 ( z ) ⋅ z − 3 G(z) = \underbrace{\frac{0.1813}{1 - 0.8187 z^{-1}}}_{G_0(z)} \cdot z^{-3} G(z)=G0(z)
1−0.8187z−10.1813⋅z−3
所以, d = 3 d=3 d=3 且 G 0 ( z ) = 0.1813 1 − 0.8187 z − 1 G_0(z) = \frac{0.1813}{1 - 0.8187 z^{-1}} G0(z)=1−0.8187z−10.1813。
代入最少拍控制器公式:
D ( z ) = 1 G 0 ( z ) ( 1 − z − d ) = 1 ( 0.1813 1 − 0.8187 z − 1 ) ( 1 − z − 3 ) D(z) = \frac{1}{G_0(z)(1 - z^{-d})} = \frac{1}{(\frac{0.1813}{1 - 0.8187 z^{-1}})(1 - z^{-3})} D(z)=G0(z)(1−z−d)1=(1−0.8187z−10.1813)(1−z−3)1
D ( z ) = 1 − 0.8187 z − 1 0.1813 ( 1 − z − 3 ) ≈ 5.5157 ( 1 − 0.8187 z − 1 ) 1 − z − 3 D(z) = \frac{1 - 0.8187 z^{-1}}{0.1813(1 - z^{-3})} \approx \frac{5.5157(1 - 0.8187 z^{-1})}{1 - z^{-3}} D(z)=0.1813(1−z−3)1−0.8187z−1≈1−z−35.5157(1−0.8187z−1)
答案2:
对于大林控制器,首先计算参数 a a a:
T = 1 T=1 T=1, λ = 4 \lambda=4 λ=4。
a = e − T / λ = e − 1 / 4 = e − 0.25 ≈ 0.7788 a = e^{-T/\lambda} = e^{-1/4} = e^{-0.25} \approx 0.7788 a=e−T/λ=e−1/4=e−0.25≈0.7788。
期望的闭环响应为:
Φ d e s ( z ) = ( 1 − a ) z − ( d + 1 ) 1 − a z − 1 = ( 1 − 0.7788 ) z − ( 3 + 1 ) 1 − 0.7788 z − 1 = 0.2212 z − 4 1 − 0.7788 z − 1 \Phi_{des}(z) = \frac{(1-a)z^{-(d+1)}}{1-az^{-1}} = \frac{(1-0.7788)z^{-(3+1)}}{1-0.7788z^{-1}} = \frac{0.2212 z^{-4}}{1-0.7788z^{-1}} Φdes(z)=1−az−1(1−a)z−(d+1)=1−0.7788z−1(1−0.7788)z−(3+1)=1−0.7788z−10.2212z−4。
代入万能钥匙公式 D ( z ) = Φ d e s ( z ) G ( z ) ( 1 − Φ d e s ( z ) ) D(z) = \frac{\Phi_{des}(z)}{G(z)(1 - \Phi_{des}(z))} D(z)=G(z)(1−Φdes(z))Φdes(z) 进行化简,或者直接使用推导出的最终公式:
D ( z ) = ( 1 − a ) z − 1 G 0 ( z ) ( 1 − a z − 1 − ( 1 − a ) z − ( d + 1 ) ) D(z) = \frac{(1-a)z^{-1}}{G_0(z)(1 - az^{-1} - (1-a)z^{-(d+1)})} D(z)=G0(z)(1−az−1−(1−a)z−(d+1))(1−a)z−1
D ( z ) = ( 1 − 0.7788 ) z − 1 ( 0.1813 1 − 0.8187 z − 1 ) ( 1 − 0.7788 z − 1 − ( 1 − 0.7788 ) z − 4 ) D(z) = \frac{(1-0.7788)z^{-1}}{(\frac{0.1813}{1 - 0.8187 z^{-1}})(1 - 0.7788z^{-1} - (1-0.7788)z^{-4})} D(z)=(1−0.8187z−10.1813)(1−0.7788z−1−(1−0.7788)z−4)(1−0.7788)z−1
D ( z ) = 0.2212 z − 1 ( 1 − 0.8187 z − 1 ) 0.1813 ( 1 − 0.7788 z − 1 − 0.2212 z − 4 ) ≈ 1.22 z − 1 ( 1 − 0.8187 z − 1 ) 1 − 0.7788 z − 1 − 0.2212 z − 4 D(z) = \frac{0.2212 z^{-1} (1 - 0.8187 z^{-1})}{0.1813 (1 - 0.7788z^{-1} - 0.2212z^{-4})} \approx \frac{1.22 z^{-1} (1 - 0.8187 z^{-1})}{1 - 0.7788z^{-1} - 0.2212z^{-4}} D(z)=0.1813(1−0.7788z−1−0.2212z−4)0.2212z−1(1−0.8187z−1)≈1−0.7788z−1−0.2212z−41.22z−1(1−0.8187z−1)
答案3:
这种现象最可能是采样间纹波(Intersample Ripple)。
最少拍控制器为了在采样时刻达到完美输出,可能会迫使控制量在两个采样点之间剧烈波动,导致执行器过度磨损。
是的,我会考虑切换到大林控制器。
原因是:大林算法通过引入可调的响应时间常数 λ \lambda λ,允许我们牺牲一点响应速度来换取整个控制过程的平滑性。通过选择一个合适的 λ \lambda λ(比如本例中的4秒),可以显著降低控制量的波动幅度,避免采样间纹波,保护执行器,并使整个系统运行更稳定、更鲁棒,这在实际工业应用中通常是更重要的考量。