前言
本次仅是对于当时没写出来的题进行补题
A、隔板
题目传送门:隔板
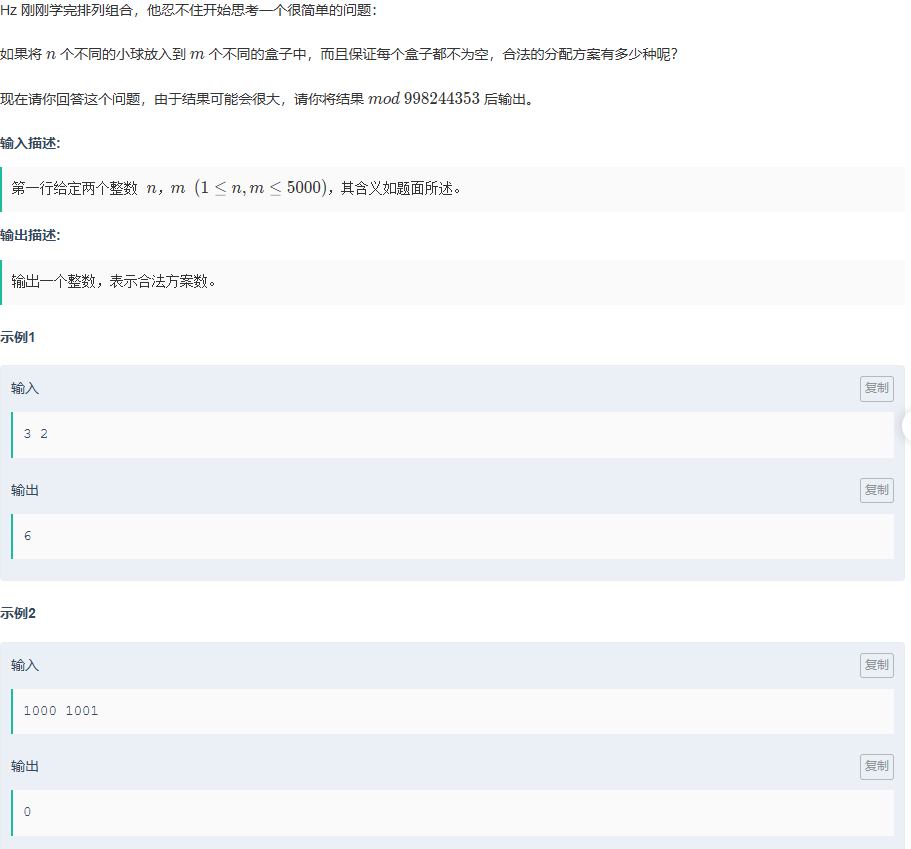
对于这一题利用到了第二类斯特林数
其定义:



完整代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e4;
ll dp[N][N];
ll sum[N];
ll mod=998244353;
void solve()
{
ll n,m;
cin>>n>>m;
sum[1]=1;
sum[0]=1;
if(n<m)
{
cout<<0<<endl;
return ;
}
for(ll i=1;i<=m;i++)
{
sum[i]=sum[i-1]*i%mod;
}
dp[0][0]=1;
for(ll i=1;i<=n;i++)
{
for(ll j=1;j<=m;j++)
{
dp[i][j]=(dp[i-1][j-1]+dp[i-1][j]*j)%mod;//以第二类斯特林数推出
}
}
cout<<dp[n][m]*sum[m]%mod<<endl;//最后还要乘上m!
}
signed main()
{
IOS;
ll t=1;
// cin>>t;
while(t--)
{
solve();
}
return 0;
}
至于为什么要乘上m的阶乘,

考虑到顺序,故要乘上m的阶乘
B、代价转移
题目传送门:代价转移
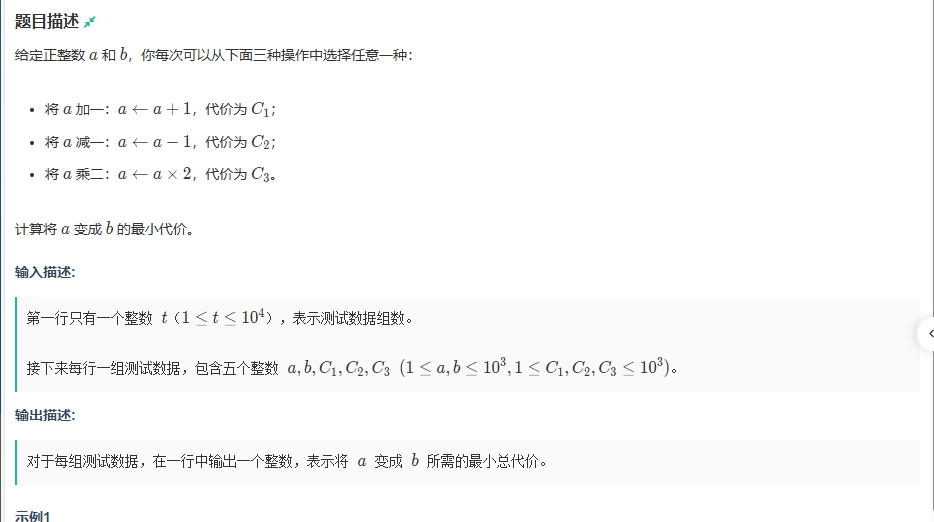
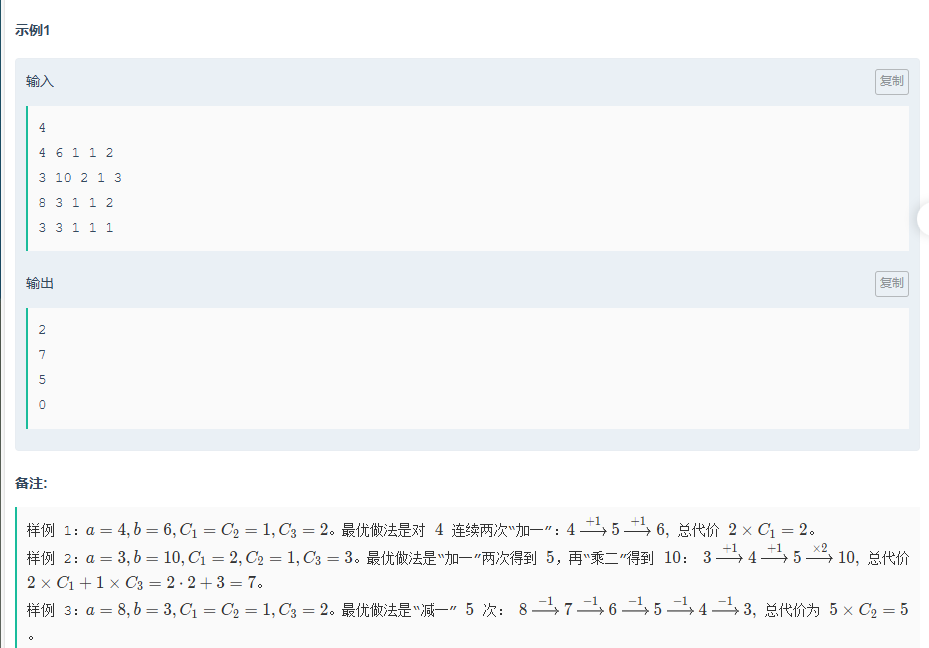
对于这一题利用到了类似 Dijkstra 算法的操作
把从初始值 a 到目标值 b 的过程,看作在数值状态空间中找最小代价路径的问题,每个数值是图中的节点,操作是有向边,边权是操作代价。
完整代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll> // 定义二元组类型,用于存储{代价, 数值}
const ll N=1e4+10;
ll a[N]; // 存储到达每个数值位置的最小代价,初始为极大值
void solve()
{
ll a1, b, c1, c2, c3;
cin >> a1 >> b >> c1 >> c2 >> c3;
if(a1 == b) { // 特殊情况:初始值等于目标值,无需任何操作
cout << 0 << endl;
return;
}
// 初始化代价数组为极大值(0x3f3f3f3f),表示初始不可达
memset(a, 0x3f3f3f, sizeof a);
// 使用优先队列(小顶堆)优化搜索,每次取出当前代价最小的状态
priority_queue<pii, vector<pii>, greater<pii>> p;
p.push({0, a1}); // 将初始状态{代价0, 数值a1}加入队列
while(p.size()) {
pii current = p.top(); // 取出当前代价最小的状态
p.pop();
ll cost = current.first; // 当前路径的总代价
ll value = current.second; // 当前到达的数值
if(value == b) { // 成功到达目标数值,输出最小代价
cout << cost << endl;
return;
}
// 如果当前代价大于已记录的最小代价,跳过该状态(剪枝优化)
if(cost > a[value]) continue;
// 操作1:数值加1,代价为c1
if(value + 1 < N && cost + c1 < a[value + 1]) {
a[value + 1] = cost + c1; // 更新最小代价
p.push({a[value + 1], value + 1}); // 将新状态加入队列
}
// 操作2:数值减1,代价为c2
if(value - 1 > 0 && cost + c2 < a[value - 1]) {
a[value - 1] = cost + c2; // 更新最小代价
p.push({a[value - 1], value - 1}); // 将新状态加入队列
}
// 操作3:数值乘2,代价为c3
if(value * 2 < N && cost + c3 < a[value * 2]) {
a[value * 2] = cost + c3; // 更新最小代价
p.push({a[value * 2], value * 2}); // 将新状态加入队列
}
}
}
signed main()
{
IOS;
ll t = 1;
cin >> t;
while(t--) {
solve();
}
return 0;
}
G,最大子段和,但是两段
题目传送门:最大子段和,但是两段


对于这一题,要找两段最大和,可先向右每次记录下来该点的最大值,同样从右向左找最大值然后记录下来
完整代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll s[N]; // 存储原始数组
ll s1[N]; // 存储从左到右的最大子段和
ll s2[N]; // 存储从右到左的最大子段和
void solve()
{
ll n;
cin>>n;
for(ll i=1;i<=n;i++)
{
cin>>s[i];
}
// 计算从左到右的最大子段和(正向DP)
ll a=INT_MIN; // 当前位置结尾的最大子段和
ll b=INT_MIN; // 全局最大子段和
for(ll i=1;i<=n;i++)
{
// 状态转移:当前位置结尾的最大子段和 = max(当前元素, 前一个位置的最大子段和+当前元素)
a=max(s[i],a+s[i]);
// 更新全局最大子段和
b=max(a,b);
// 记录到i位置为止的全局最大子段和
s1[i]=b;
}
// 计算从右到左的最大子段和(反向DP)
a=INT_MIN;
b=INT_MIN;
for(ll i=n;i>=1;i--)
{
// 同理,从右向左计算
a=max(s[i],a+s[i]);
b=max(a,b);
// 记录从i位置开始到结尾的全局最大子段和
s2[i]=b;
}
// 枚举分割点,找到最大和
ll ans=-1e18; // 初始化为极小值
for(ll i=1;i<n;i++)
{
// 分割点为i时的最大和 = 前i个元素的最大子段和 + 后n-i个元素的最大子段和
ans=max(ans,s1[i]+s2[i+1]);
}
cout<<ans<<endl;
}
signed main()
{
IOS;
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
H,黑客帝国
题目传送门:黑客帝国
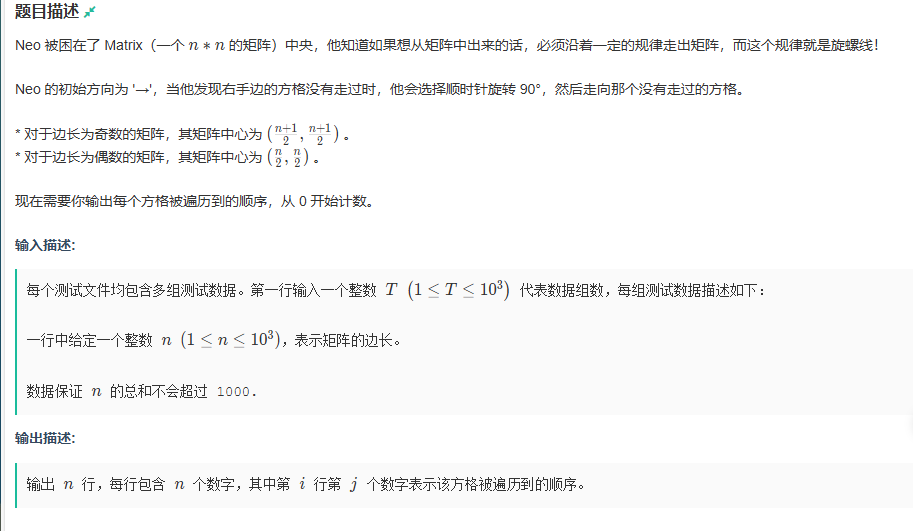

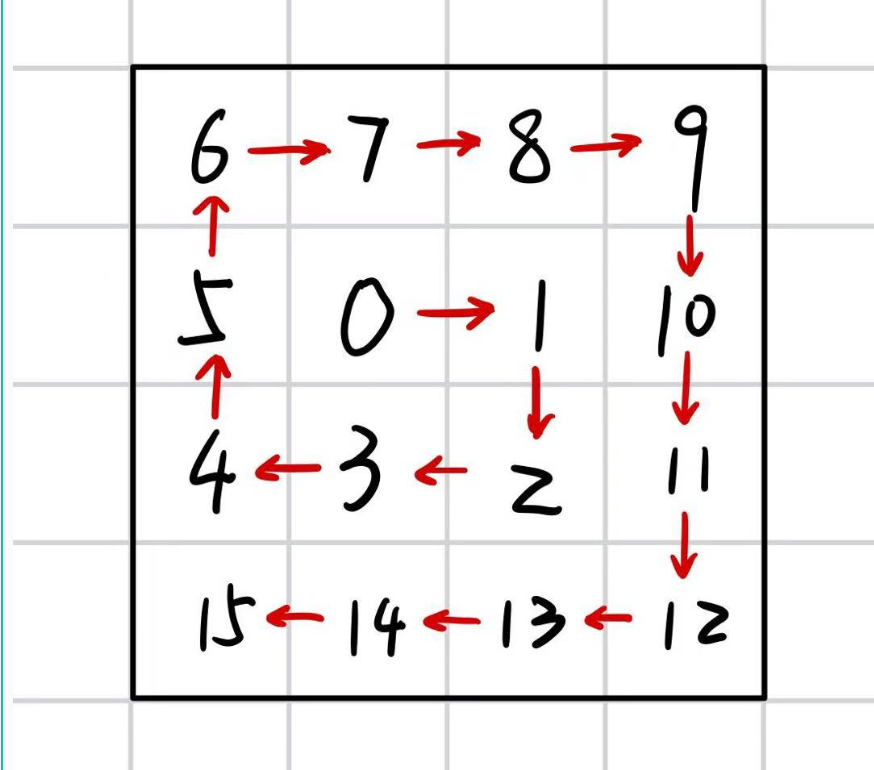
纯模拟,恶心
完整代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e4+10;
ll s[N][N];
ll dx[]={0,1,0,-1},dy[]={1,0,-1,0};
void solve()
{
ll n;
cin>>n;
if(n==1)
{
cout<<0<<endl;
return ;
}
ll x=0,y=0;
if(n&1)
x=(n+1)/2-1,y=(n+1)/2-1;
else
x=n/2-1,y=n/2-1;
ll d=0,l=1,sum=0;
s[x][y]=sum++;
while(sum<n*n)
{
for(ll i=1;i<=2;i++)
{
for(ll j=0;j<l;j++)
{
x=x+dx[d];
y=y+dy[d];
if(x>=0&&x<n&&y>=0&&y<n)
s[x][y]=sum++;
}
d=(d+1)%4;
}
l++;
}
for(ll i=0;i<n;i++)
{
for(ll j=0;j<n;j++)
cout<<s[i][j]<<" ";
cout<<endl;
}
}
signed main()
{
IOS;
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
I,二进制转化
题目传送门:二进制转化


通过手动操作一下会发现,当首尾相同时,肯定相同
其次就是判断l与r了如果有一个在边界,则一定也行
代码:
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
void solve()
{
ll n;
cin>>n;
string s;
cin>>s;
ll l,r;
cin>>l>>r;
if(s[0]==s[n-1])
{
cout<<"Yes"<<endl;
return ;
}
if(l==1||r==n)
{
cout<<"Yes"<<endl;
return ;
}
cout<<"No"<<endl;
}
signed main()
{
IOS;
ll t=1;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
M,无聊的子序列
题目传送门:无聊的子序列
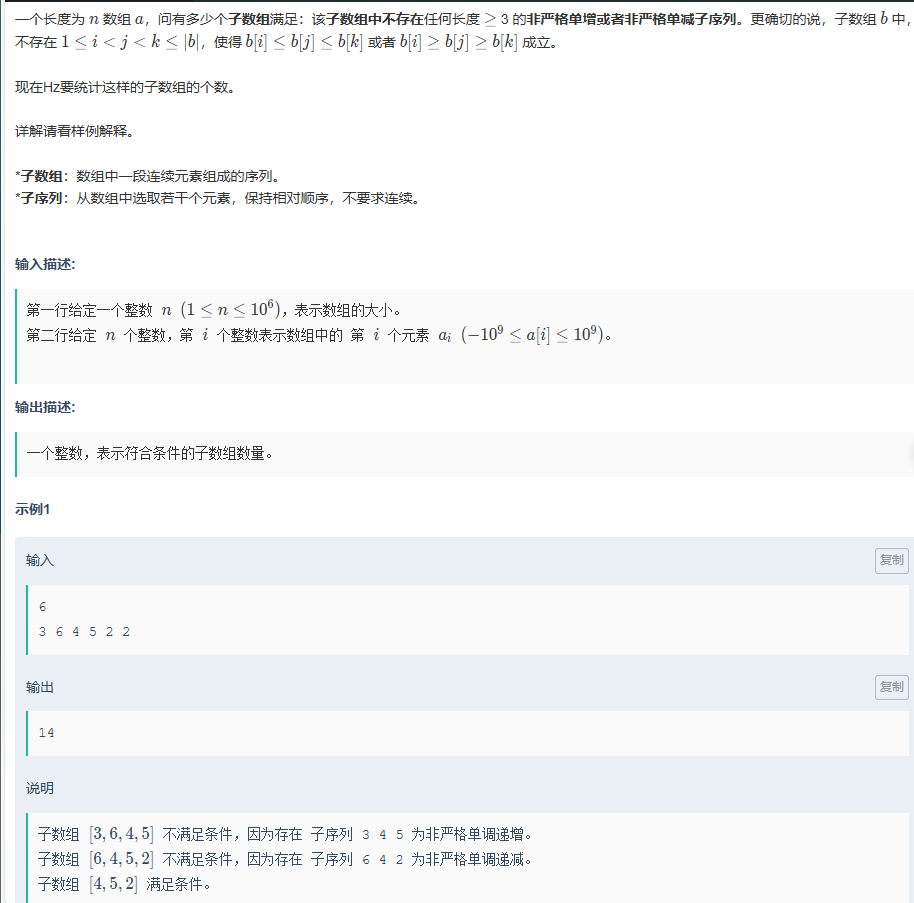
这一题同样是找规律,当你打表之后会发现当长度大于5的时候是一定不成立的,因此只需要考虑长度小于等于4的子数组
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
const ll N=1e6+10;
ll s[N];
void solve()
{
ll n;
cin>>n;
for(ll i=1;i<=n;i++)
{
cin>>s[i];
}
ll ans=2*n-1;//长度为1的还有长度为2的一定成立
if(n==1)//特判长度为1的
{
cout<<1<<endl;
return ;
}
for(ll i=1;i<=n-2;i++)//判断长度为3的
{
if(s[i+1]<=s[i]&&s[i+2]<=s[i+1])
continue;
if(s[i+1]>=s[i]&&s[i+2]>=s[i+1])
continue;
ans++;
}
for(ll i=1;i<=n-3;i++)//判断长度为4的
{
ll a=s[i];
ll b=s[i+1];
ll c=s[i+2];
ll d=s[i+3];
if(a>=b&&(b>=c||b>=d)||a<=b&&(b<=c||b<=d))
continue;
if(d>=c&&(c>=b||c>=a)||d<=c&&(c<=b||c<=a))
continue;
ans++;
}
cout<<ans<<endl;
}
signed main()
{
IOS;
ll t=1;
while(t--)
{
solve();
}
return 0;
}
总结
这次萌新赛,没啥说的,很大一部分是由于自己的编码能力太弱,其次是对于动态规划以及预处理了解的太少了