L0 范数、L1 范数和 L2 范数详解(归一化+正则化)-EW帮帮网

在机器学习和深度学习领域，L1 和 L2 是两种常见的范数（Norm），主要用于衡量向量的大小，并且在正则化、特征选择以及优化算法等方面都有广泛应用。下面为你详细介绍它们的定义、区别以及设置方法。

L0 范数、L1 范数和 L2 范数的定义

对于一个向量:

L0 范数：向量中非零元素的个数。
L1 范数（曼哈顿距离）：向量元素绝对值的和，公式为。
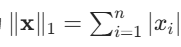L2 范数（欧几里得距离）：向量元素平方和的平方根，公式为

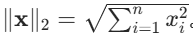
L1 和 L2 的主要区别

特性	L1 范数	L2 范数
几何意义	曼哈顿距离（城市街区距离）	欧几里得距离（直线距离）
函数图像	在原点处不可导，呈棱形	处处可导，呈圆形
稀疏性	会使参数向量变得稀疏，常用于特征选择	参数趋向于均匀分布，不会产生稀疏解
抗噪性	对异常值更鲁棒	对异常值敏感
应用场景	Lasso 回归、特征选择、压缩感知	Ridge 回归、权重衰减、正则化

在深度学习中的应用

1. 归一化（Normalization）

L1 归一化：将向量的 L1 范数缩放为 1，即每个元素除以所有元素绝对值的和。
```
import torch
x = torch.tensor([1.0, -2.0, 3.0])
x_l1 = torch.nn.functional.normalize(x, p=1, dim=0)  # 输出: [0.1667, -0.3333, 0.5000]
```
L2 归一化：将向量的 L2 范数缩放为 1，即每个元素除以所有元素平方和的平方根。
```
x_l2 = torch.nn.functional.normalize(x, p=2, dim=0)  # 输出: [0.2673, -0.5345, 0.8018]
```
2. 正则化（Regularization）

L1 正则化：在损失函数中添加参数绝对值的和，公式为

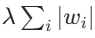
# 在PyTorch中手动实现L1正则化
l1_lambda = 0.001
l1_reg = l1_lambda * sum(p.abs().sum() for p in model.parameters())
loss = original_loss + l1_reg

L2 正则化（权重衰减）：在损失函数中添加参数平方和，公式为

# 在优化器中直接设置weight_decay参数（等价于L2正则化）
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, weight_decay=0.001)

3. 优化算法

L1 优化：由于 L1 在原点处不可导，通常使用近端梯度下降（Proximal Gradient Descent）等特殊算法。
L2 优化：可以直接使用梯度下降等标准优化算法。

如何选择 L1 还是 L2？

需要稀疏解时：选择 L1 正则化。比如在特征选择任务中，它能让不重要的特征权重变为 0。
需要平滑解时：选择 L2 正则化。它有助于防止过拟合，提高模型的泛化能力。
处理高维数据时：L1 可以有效减少特征维度；而 L2 在处理相关特征时表现更好。
对异常值敏感时：L1 的鲁棒性更强；L2 则可能会受到异常值的较大影响。

常见问题解答

L1 为什么会产生稀疏解？
- L1 的损失函数在原点处有 “棱角”，优化过程中更容易使参数更新到零点。
L2 为什么能防止过拟合？
- L2 会惩罚较大的权重，使模型更加平滑，从而减少对训练数据噪声的拟合。
能否同时使用 L1 和 L2？
- 可以，这种方法称为 Elastic Net，它结合了 L1 和 L2 的优点。
```
# Elastic Net损失函数
elastic_net_loss = original_loss + l1_lambda * l1_reg + l2_lambda * l2_reg
```
  通过合理选择 L1 或 L2 范数，你可以根据具体的任务需求来调整模型的性能和行为。

1.归一化操作的默认范数

PyTorch：torch.nn.functional.normalize 函数的默认范数为 L2（通过 p=2 参数指定）。

# 默认使用L2范数归一化
normalized_x = F.normalize(x, dim=-1)  # 等价于 F.normalize(x, p=2, dim=-1)

TensorFlow：tf.nn.l2_normalize 函数直接实现 L2 归一化。

2. 正则化的默认设置

权重衰减（Weight Decay）：
- 在优化器（如 Adam、SGD）中，weight_decay 参数默认值通常为 0（即不使用正则化），但当启用时，默认采用 L2 正则化。
```
# Adam优化器的weight_decay默认是0，启用后为L2正则化
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, weight_decay=0.001)
```
- L1 正则化：需要手动实现（如通过循环参数计算绝对值和），没有直接的默认设置。

3. 机器学习模型的默认选择

线性回归：
- Ridge 回归（L2 正则化）是更常见的默认选择（如 sklearn.linear_model.Ridge）。
- Lasso 回归（L1 正则化）需要显式指定（如 sklearn.linear_model.Lasso）。
深度学习框架：
- 大多数预训练模型（如 BERT、ResNet）默认使用 Batch Normalization 和 Dropout 来正则化，而非显式的 L1/L2。

为什么 L2 更常用？

数学性质优良：L2 范数处处可导，优化算法（如梯度下降）更容易处理。
防止过拟合：通过惩罚大权重，使模型更平滑，泛化能力更强。
计算效率高：L2 正则化可以直接嵌入到优化器中（如权重衰减），无需额外计算。
对异常值敏感：在大多数场景下，异常值可能包含有价值的信息，L2 不会像 L1 那样直接忽略它们。

何时需要手动指定 L1？

特征选择：希望自动筛选重要特征（通过将不重要特征的权重置为 0）。
处理高维稀疏数据：如文本分类中的词袋模型。
模型压缩：生成更简洁的模型（更少的非零参数）。

总结

默认选择 L2：在没有特殊需求时，L2 是更安全的选择，能有效防止过拟合。
手动指定 L1：当需要稀疏解或特征选择时，需显式实现 L1 正则化。

如果需要同时使用 L1 和 L2，可以考虑 Elastic Net（如 sklearn.linear_model.ElasticNet）。

L0 范数、L1 范数和 L2 范数详解(归一化+正则化)