目录
时间序列预测是金融、气象、交通等领域的核心问题,其本质是通过挖掘数据中的时序规律,对未来状态进行推断。传统单一模型(如纯 LSTM 或纯 SVM)在处理复杂时序数据时往往存在局限性:LSTM 虽擅长捕捉长短期依赖,却可能因过度拟合时序噪声导致泛化能力不足;SVM 虽在非线性映射上表现优异,却难以直接处理原始时序序列的动态特征。本文基于 “LSTM+SVM” 混合模型的实现逻辑,从理论层面阐述其设计原理、协同机制及应用价值,揭示混合模型如何突破单一模型的瓶颈。
1、单一模型的局限性:混合架构的设计动机
时间序列数据的核心挑战在于时序依赖性与非线性特征的双重复杂性。单一模型在应对这一挑战时存在明显短板:
| 模型类型 | 核心优势 | 局限性 |
|---|---|---|
| LSTM(深度学习) | 1. 通过门控机制捕捉长短期时序依赖 2. 自动学习时序特征的动态演化规律 |
1. 对噪声敏感,易过度拟合时序波动 2. 高维输出特征的非线性映射能力有限 3. 训练需大量数据,小样本场景泛化性差 |
| SVM(传统机器学习) | 1. 通过核函数实现低维到高维的非线性映射 2. 基于结构风险最小化,小样本泛化能力强 3. 对高维特征的冗余信息不敏感 |
1. 无法直接处理原始时序序列的动态依赖 2. 依赖人工特征工程,难以捕捉时序深层规律 |
混合模型的设计逻辑正是 “取长补短”:利用 LSTM 的时序特征提取能力处理动态依赖,再通过 SVM 的非线性拟合能力优化预测精度,形成 “特征提取 — 非线性映射” 的二级处理流程。
2、LSTM 的时序特征提取:从原始序列到高阶表征
LSTM(长短期记忆网络)作为循环神经网络(RNN)的变种,其核心价值在于通过门控机制解决传统 RNN 的 “梯度消失” 问题,实现对长序列依赖的有效捕捉。在混合模型中,LSTM 的角色是 “时序特征提取器”,其工作原理可分解为三个层次:
2.1、门控机制的时序过滤能力
LSTM 通过遗忘门、输入门和输出门的协同作用,动态筛选时序信息:
- 遗忘门:过滤无关历史噪声(如股票价格的短期随机波动);
- 输入门:保留关键新信息(如突发政策对价格的影响);
- 输出门:生成当前时间步的有效特征表示。
这种机制使 LSTM 能从原始序列(如代码中的收盘价、成交量、波动率)中提炼出蕴含时序规律的高阶特征(如趋势延续性、波动聚集性)。
2.2、隐藏状态的特征压缩作用
在代码实现中,LSTM 的最终输出是 “最后一层隐藏状态”(hn[-1]),其维度由hidden_size(如 64)控制。这一过程本质是特征压缩:将长度为 20 的原始序列(sequence_length=20)和 5 维特征(收盘价、MA10 等)压缩为 64 维的紧凑向量,既保留核心时序模式,又降低后续模型的计算复杂度。
2.3、预训练的特征优化逻辑
代码中 LSTM 通过全连接层(nn.Linear(hidden_size, 1))与 MSE 损失函数进行预训练,其目的并非直接预测,而是引导 LSTM 学习 “对预测有价值的特征”。这种 “有监督的特征学习” 确保提取的隐藏状态与目标变量(如收盘价)存在强相关性,为后续 SVM 的预测奠定基础。
3、SVM 的非线性映射:从高阶特征到预测输出
SVM(支持向量机)通过核函数实现低维特征到高维空间的非线性映射,在混合模型中承担 “最终预测器” 的角色。其与 LSTM 的协同逻辑体现在三个方面:
3.1、核函数对非线性关系的建模能力
代码中采用 RBF(径向基函数)核,其本质是通过非线性变换将 LSTM 输出的 64 维特征映射到更高维空间,使原本线性不可分的特征关系变得可分。例如,股票价格的 “趋势反转” 往往依赖于 “波动率放大 + 成交量骤增” 的联合条件,SVM 能通过核函数捕捉这种复杂交互特征,而 LSTM 单独预测时易忽略此类非线性组合。
3.2、小样本场景下的泛化优势
SVM 基于 “结构风险最小化” 原则,通过最大化分类间隔(回归场景中为最小化 ε- 不敏感损失)降低过拟合风险。在金融时间序列等小样本场景中(如代码中仅 500 条数据),SVM 能有效利用 LSTM 提取的紧凑特征,避免深度学习模型对数据量的过度依赖。
3.3、对冗余特征的 “免疫性”
LSTM 输出的高阶特征可能包含少量冗余信息(如重复的趋势特征),而 SVM 通过支持向量的选择机制,仅关注对预测起关键作用的特征组合,进一步提升模型的稳健性。
4、混合模型的协同机制:1+1>2 的核心逻辑
LSTM 与 SVM 的融合并非简单拼接,而是通过 “时序特征提取 — 非线性映射” 的流水线式协同,实现对时间序列复杂性的分层破解。其核心机制可概括为三个层面:
4.1、特征传递的层级性
原始数据(如收盘价、成交量)首先经 LSTM 处理,转化为蕴含时序规律的高阶特征(隐藏状态),再传递给 SVM 进行最终预测。这种 “原始数据→时序特征→预测结果” 的层级传递,使模型能分阶段处理数据的不同属性:LSTM 专注于 “时序动态性”,SVM 专注于 “特征非线性”,避免单一模型同时应对双重复杂性。
4.2、误差矫正的互补性
LSTM 的预测误差往往源于对短期噪声的过度拟合,而 SVM 的误差多源于对长周期趋势的捕捉不足。混合模型中,LSTM 的高阶特征过滤了部分噪声,SVM 的核函数又强化了对趋势的非线性建模,两者误差形成互补,最终降低整体预测偏差(如代码中通过 MSE 和 R² 评估的优化效果)。
4.3、计算效率的平衡性
LSTM 的训练复杂度随序列长度呈线性增长,而 SVM 的复杂度随样本量呈平方增长。混合模型中,LSTM 的特征压缩(如 64 维隐藏状态)大幅降低了 SVM 的输入维度,在保证精度的同时平衡了计算成本,使模型更适用于实时预测场景(如高频交易中的价格预测)。
5、应用场景与理论延伸
LSTM+SVM 混合模型的理论框架不仅适用于金融时间序列,还可推广至其他时序预测领域:
- 气象预测:LSTM 提取气温、湿度的时序依赖,SVM 捕捉 “温度 - 降水” 的非线性关系;
- 交通流量预测:LSTM 学习早晚高峰的周期性规律,SVM 建模特殊事件(如节假日)的突发波动;
- 工业故障预测:LSTM 挖掘设备传感器数据的趋势变化,SVM 识别 “振动 - 温度” 的异常关联。
6、完整代码
"""
文件名: LSTM+SVM
作者: 墨尘
日期: 2025/7/27
项目名: d2l_learning
备注: 基于LSTM和SVM的混合模型进行时间序列预测,结合了深度学习和传统机器学习的优势
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import torch
import torch.nn as nn
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, r2_score
# 设置中文字体,确保图表中的中文正常显示
plt.rcParams["font.family"] = ["SimHei"] # 指定默认中文字体
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示问题
class LSTMFeatureExtractor(nn.Module):
"""LSTM特征提取器:将时序数据转换为固定维度的特征向量,用于后续的SVM回归"""
def __init__(self, input_size, hidden_size, num_layers=1, dropout=0.0):
"""
初始化LSTM特征提取器
参数:
input_size: 输入特征的维度
hidden_size: LSTM隐藏层的维度
num_layers: LSTM层数
dropout: Dropout概率,用于防止过拟合
"""
super().__init__()
# 定义LSTM层,batch_first=True表示输入格式为(batch, seq_len, feature)
self.lstm = nn.LSTM(
input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True,
dropout=dropout,
bidirectional=False # 使用单向LSTM
)
# 添加全连接层,将LSTM的隐藏状态映射到与目标变量相同的维度
# 这用于训练LSTM学习有意义的特征表示
self.fc = nn.Linear(hidden_size, 1)
def forward(self, x):
"""
前向传播函数,定义数据如何通过网络
参数:
x: 输入张量,形状为(batch_size, sequence_length, input_size)
返回:
output: 预测值,形状为(batch_size, 1)
"""
# LSTM的输出格式为(output, (h_n, c_n))
# output: 每个时间步的隐藏状态,形状为(batch_size, seq_len, hidden_size)
# h_n: 最后一个时间步的隐藏状态,形状为(num_layers, batch_size, hidden_size)
# c_n: 最后一个时间步的细胞状态,形状同上
_, (hn, _) = self.lstm(x)
# 提取最后一层的隐藏状态,形状调整为(batch_size, hidden_size)
last_hidden = hn[-1]
# 通过全连接层得到最终输出,形状为(batch_size, 1)
output = self.fc(last_hidden)
return output
def create_sequences(df, target_col="Close", seq_len=20):
"""
将时间序列数据转换为监督学习格式(序列-目标对)
参数:
df: 包含特征的DataFrame
target_col: 目标变量列名
seq_len: 序列长度(用于预测的历史时间步数)
返回:
X: 特征序列,形状为(samples, seq_len, features)
y: 目标值,形状为(samples,)
"""
X, y = [], []
for i in range(seq_len, len(df)):
X.append(df.iloc[i - seq_len:i].values) # 历史特征序列
y.append(df.iloc[i][target_col]) # 对应的目标值
return np.array(X), np.array(y)
def plot_training_loss(losses, epochs):
"""可视化训练过程中的损失变化"""
plt.figure(figsize=(10, 5))
plt.plot(range(epochs), losses, 'b-', linewidth=2)
plt.title('训练损失变化')
plt.xlabel('Epoch')
plt.ylabel('损失值 (MSE)')
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('training_loss.png') # 保存图表
plt.close()
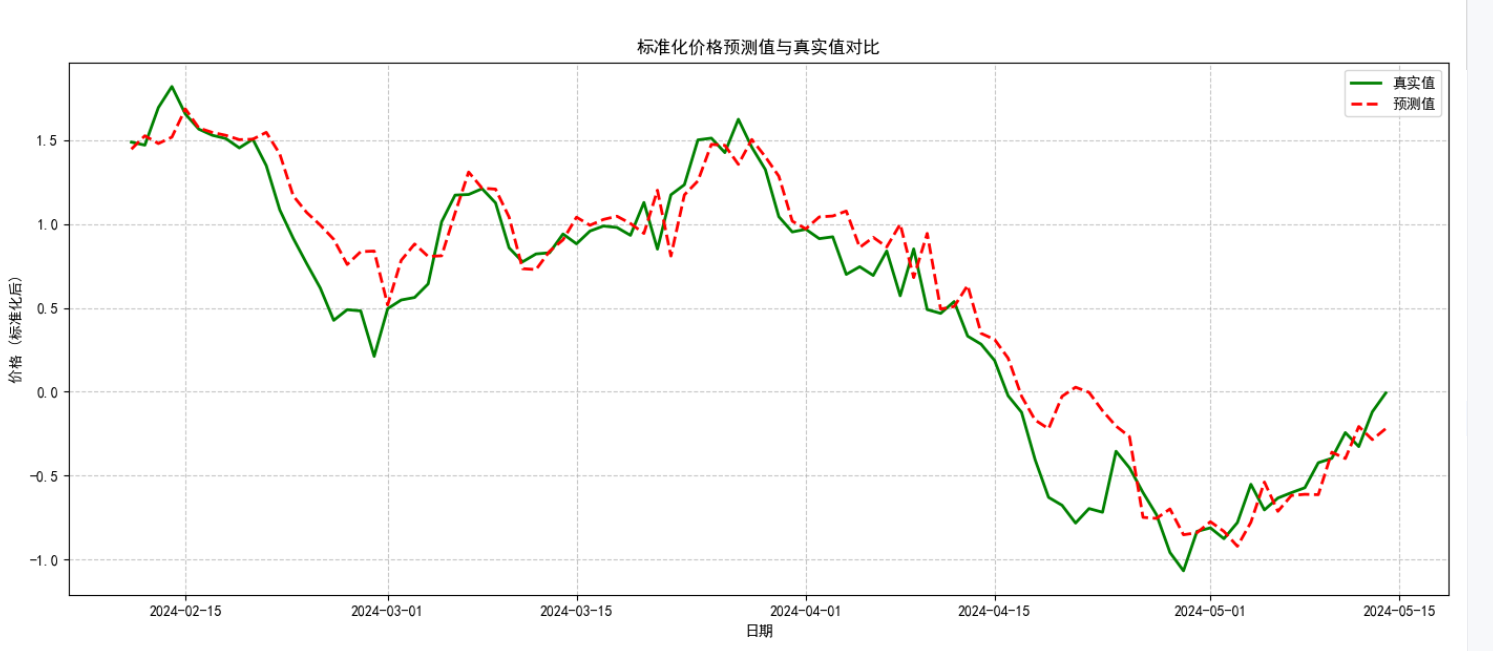
def plot_prediction_vs_actual(dates, actual, predicted, title="预测值与真实值对比"):
"""可视化预测结果与真实值对比"""
plt.figure(figsize=(14, 6))
plt.plot(dates, actual, 'g-', label='真实值', linewidth=2)
plt.plot(dates, predicted, 'r--', label='预测值', linewidth=2)
plt.title(title)
plt.xlabel('日期')
plt.ylabel('价格 (标准化后)')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('prediction_results.png') # 保存图表
plt.close()
def main():
"""主函数:协调数据处理、模型训练和评估的整个流程"""
# 步骤1: 生成虚拟金融数据
print("正在生成虚拟金融数据...")
date_range = pd.date_range(start="2023-01-01", periods=500, freq="D")
price = np.cumsum(np.random.randn(500)) + 100 # 随机游走模拟股票价格
volume = np.random.randint(100, 1000, size=500) # 随机成交量
data = pd.DataFrame({
"Date": date_range,
"Close": price,
"Volume": volume
}).set_index("Date") # 设置日期为索引
# 步骤2: 添加技术指标
print("正在计算技术指标...")
data["MA10"] = data["Close"].rolling(window=10).mean() # 10日移动平均线
data["Return"] = data["Close"].pct_change() # 每日收益率
data["Volatility"] = data["Return"].rolling(window=10).std() # 10日滚动波动率
data.dropna(inplace=True) # 删除包含NaN的行,确保数据完整性
# 步骤3: 数据可视化
print("正在生成数据可视化图表...")
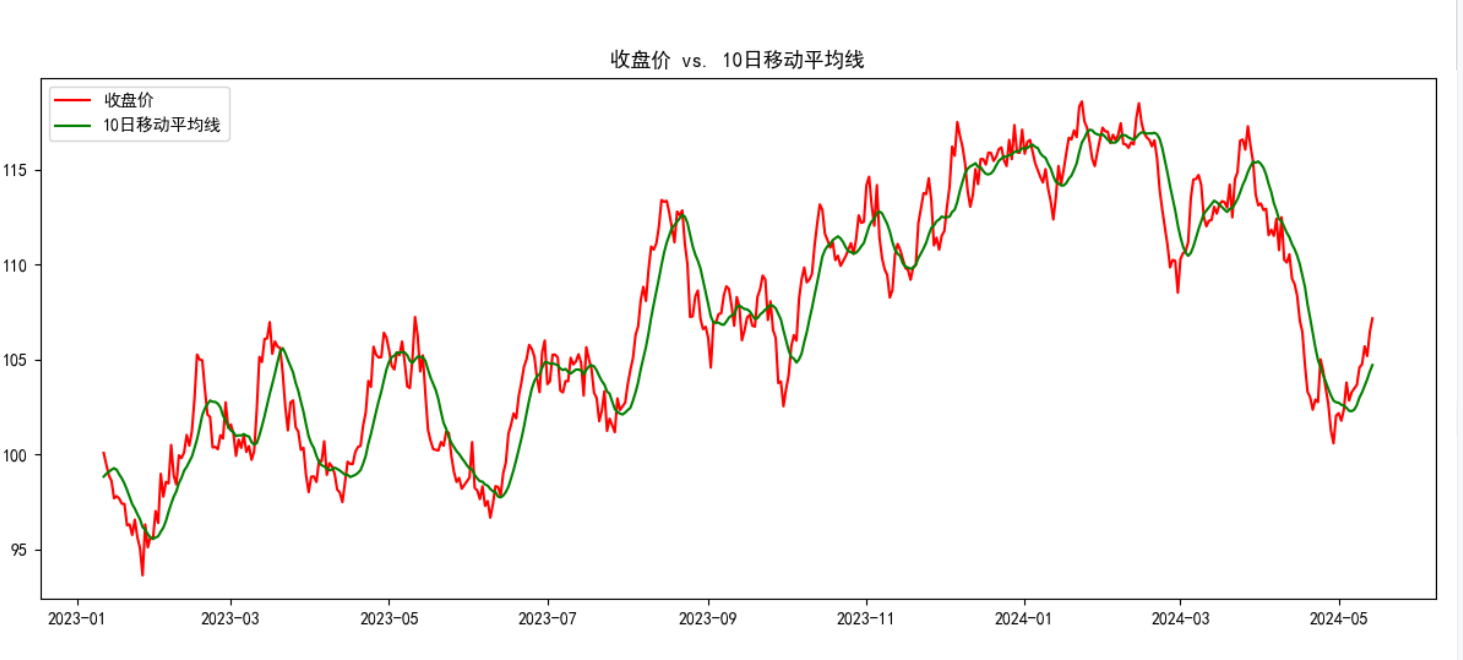
# 可视化1: 收盘价与MA10
plt.figure(figsize=(12, 5))
plt.plot(data.index, data["Close"], label="收盘价", color="red")
plt.plot(data.index, data["MA10"], label="10日移动平均线", color="green")
plt.title("收盘价 vs. 10日移动平均线")
plt.legend()
plt.tight_layout()
plt.savefig("price_vs_ma10.png")
plt.close()
# 可视化2: 成交量
plt.figure(figsize=(12, 3))
plt.bar(data.index, data["Volume"], color="blue")
plt.title("成交量随时间变化")
plt.tight_layout()
plt.savefig("volume.png")
plt.close()
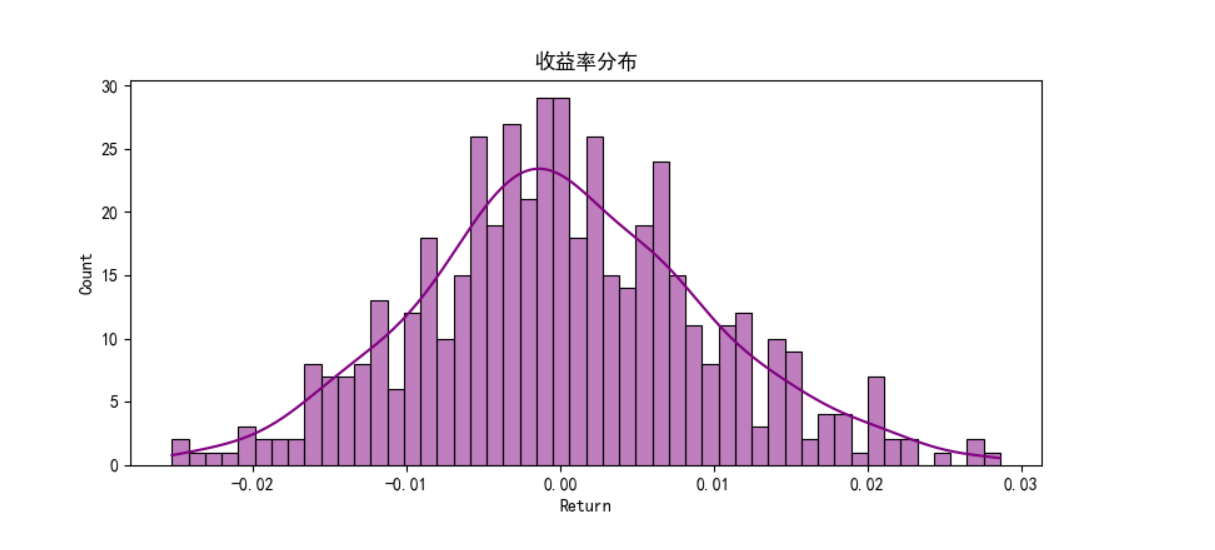
# 可视化3: 收益率分布
plt.figure(figsize=(8, 4))
sns.histplot(data["Return"], bins=50, kde=True, color="purple")
plt.title("收益率分布")
plt.tight_layout()
plt.savefig("return_distribution.png")
plt.close()
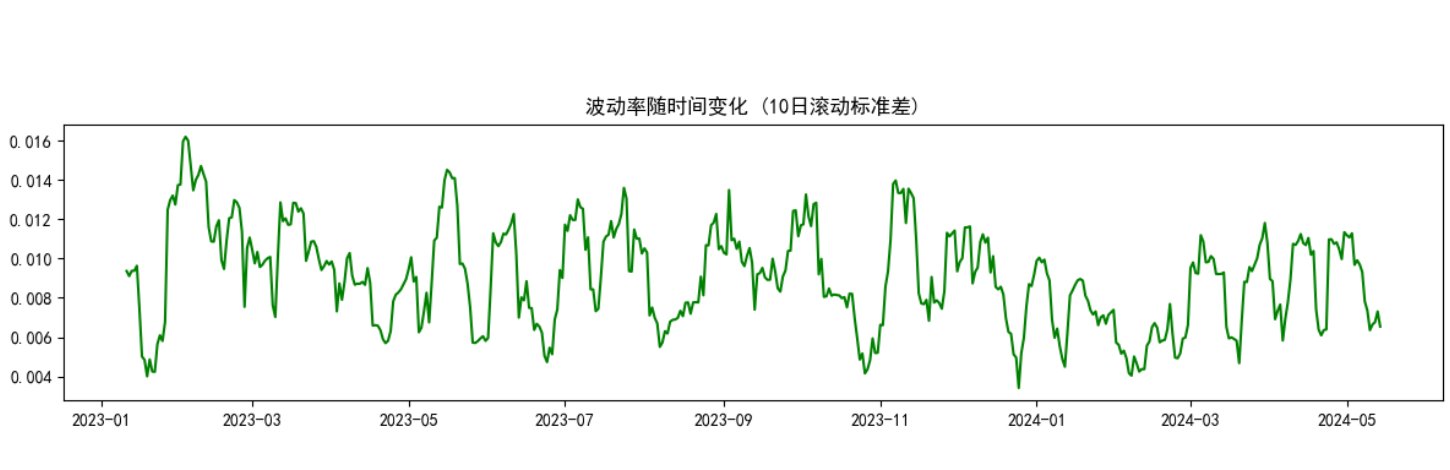
# 可视化4: 波动率
plt.figure(figsize=(12, 3))
plt.plot(data.index, data["Volatility"], color="green")
plt.title("波动率随时间变化 (10日滚动标准差)")
plt.tight_layout()
plt.savefig("volatility.png")
plt.close()
# 步骤4: 数据预处理
print("正在进行数据预处理...")
features = ["Close", "MA10", "Return", "Volatility", "Volume"] # 选择用于预测的特征
sequence_length = 20 # 使用前20天的数据预测下一天
# 数据标准化:将所有特征缩放到均值为0,标准差为1的分布
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data[features])
scaled_df = pd.DataFrame(scaled_data, index=data.index, columns=features)
# 构造序列数据:将时间序列转换为监督学习格式
X, y = create_sequences(scaled_df, "Close", sequence_length)
# 划分训练集和测试集(按时间顺序划分,保持数据的时序性)
test_size = 0.2
split_idx = int(len(X) * (1 - test_size))
X_train, X_test = X[:split_idx], X[split_idx:]
y_train, y_test = y[:split_idx], y[split_idx:]
test_dates = data.index[-len(y_test):] # 记录测试集对应的日期
print(f"训练集大小: {len(X_train)}, 测试集大小: {len(X_test)}")
# 步骤5: 转换为PyTorch张量
X_train_tensor = torch.tensor(X_train, dtype=torch.float32)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32)
# 增加一个维度,使其形状为(batch_size, 1),与模型输出匹配
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
# 步骤6: 定义并训练LSTM特征提取器
print("正在训练LSTM特征提取器...")
input_size = len(features) # 输入特征维度
hidden_size = 64 # LSTM隐藏层维度
lstm = LSTMFeatureExtractor(input_size, hidden_size)
optimizer = torch.optim.Adam(lstm.parameters(), lr=0.001) # Adam优化器
loss_fn = nn.MSELoss() # 均方误差损失函数,用于回归问题
n_epochs = 30 # 训练轮数
training_losses = [] # 记录每轮的训练损失
for epoch in range(n_epochs):
lstm.train() # 设置为训练模式
optimizer.zero_grad() # 梯度清零
output = lstm(X_train_tensor) # 前向传播
loss = loss_fn(output, y_train_tensor) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新参数
training_losses.append(loss.item())
if epoch % 5 == 0:
print(f"[Epoch {epoch+1}/{n_epochs}] Loss: {loss.item():.4f}")
# 可视化训练损失变化
plot_training_loss(training_losses, n_epochs)
# 步骤7: 提取LSTM特征
print("正在提取LSTM特征...")
lstm.eval() # 设置为评估模式
with torch.no_grad(): # 不计算梯度,节省内存和计算资源
# 提取LSTM最后一层的隐藏状态作为特征
# 这些特征将被用于训练SVM模型
_, (train_feats, _) = lstm.lstm(X_train_tensor)
train_feats = train_feats[-1].numpy() # 取最后一层的隐藏状态
_, (test_feats, _) = lstm.lstm(X_test_tensor)
test_feats = test_feats[-1].numpy()
# 步骤8: 训练SVM回归模型
print("正在训练SVM回归模型...")
# 使用RBF核函数的SVM回归器,C是正则化参数,epsilon控制允许的误差范围
svm = SVR(kernel="rbf", C=100, epsilon=0.01)
svm.fit(train_feats, y_train) # 训练SVM模型
# 步骤9: 模型评估
print("正在评估模型性能...")
predictions = svm.predict(test_feats) # 预测测试集
# 计算评估指标
mse = mean_squared_error(y_test, predictions) # 均方误差
r2 = r2_score(y_test, predictions) # 决定系数,解释方差的比例
print(f"\nSVM模型评估结果:")
print(f"MSE: {mse:.4f}, R²: {r2:.4f}")
# 步骤10: 可视化预测结果
plot_prediction_vs_actual(test_dates, y_test, predictions, "标准化价格预测值与真实值对比")
print("模型训练和评估完成!")
print("图表已保存至当前目录下的PNG文件中")
if __name__ == "__main__":
main() # 程序入口点7、实验结果
8、补充:评估模式和训练模式的区别?
8.1、评估模式与训练模式的核心区别
模型在训练和评估时的行为存在本质差异,主要体现在随机性操作的启用与否:
| 模式 | 核心特点 | 典型随机性操作 |
|---|---|---|
| 训练模式(train mode) | 启用随机性操作,用于模型参数学习 | 1. Dropout 层随机丢弃部分神经元 2. Batch Normalization 使用当前批次的均值和方差 3. 随机数据增强(如随机裁剪、翻转) |
| 评估模式(eval mode) | 关闭随机性操作,用于稳定推理 | 1. Dropout 层不丢弃神经元(保留全部特征) 2. Batch Normalization 使用训练时保存的全局均值和方差 3. 关闭数据增强(使用原始数据) |
8.2、特征提取时必须用评估模式的 3 个关键原因
8.2.1、避免特征随机性波动
训练模式中的Dropout等操作会随机丢弃部分神经元输出,导致同一输入在不同时刻提取的特征不一致。例如:
- 训练模式下,对同一图像连续提取 10 次特征,会得到 10 个略有差异的特征向量(因 Dropout 随机丢弃的神经元不同);
- 评估模式下,Dropout 关闭,同一输入始终得到相同的特征向量,保证特征的稳定性。
特征的一致性是后续任务(如分类、聚类、SVM 训练)的基础,否则会因特征波动导致下游模型学习混乱。
8.2.2、保证特征分布与训练一致
Batch Normalization(BN 层) 在训练和评估时的计算方式不同:
- 训练时,BN 层使用当前批次数据的均值和方差进行归一化;
- 评估时,BN 层使用训练过程中累计的全局均值和方差(而非当前批次的统计量)。
若特征提取时仍用训练模式,BN 层会用测试数据的批次统计量归一化特征,导致特征分布与模型训练时的分布不一致(分布偏移)。例如,训练时某特征的全局均值为 0.5,而测试批次的均值为 0.8,直接使用测试批次均值会导致特征整体偏移,影响下游任务效果。
8.2.3、确保特征完整度
训练模式中,部分层的设计是为了防止过拟合(如 Dropout),而非特征提取。例如:
- 若在特征提取时启用 Dropout,会导致部分关键特征被随机丢弃,提取的特征向量缺失重要信息;
- 评估模式下,所有神经元正常工作,能完整保留模型学到的特征表达,确保特征的完整性和代表性。