决策树实现回归任务
决策树实现回归任务就是根据特征向量来决定对应的输出值。回归树就是将特征空间划分成若干单元,每一个划分单元有一个特定的输出。因为每个结点都是“是”和“否”的判断,所以划分的边界是平行于坐标轴的。对于测试数据,我们只要按照特征将其归到某个单元,便得到对应的输出值。
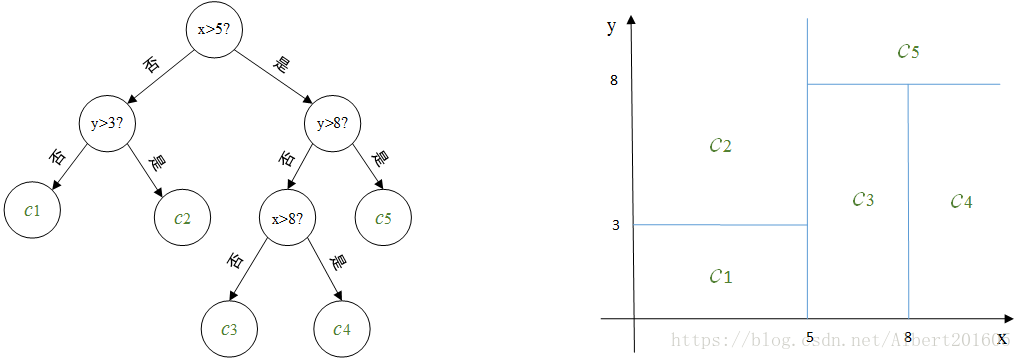
左边为对二维平面划分的决策树,右边为对应的划分示意图,其中c1,c2,c3,c4,c5是对应每个划分单元的输出。
如现在对一个新的向量(6,6)决定它对应的输出。第一维分量6介于5和8之间,第二维分量6小于8,根据此决策树很容易判断(6,6)所在的划分单元,其对应的输出值为c3.
划分的过程也就是建立树的过程,每划分一次,随即确定划分单元对应的输出,也就多了一个结点。当根据停止条件划分终止的时候,最终每个单元的输出也就确定了,也就是叶结点。
算法综述
输入:数据集D={(xi,yi)}i=1n\mathcal{D}=\{(\boldsymbol{x}_i,y_i)\}_{i=1}^nD={(xi,yi)}i=1n
输出: 回归树f(x)f(\boldsymbol{x})f(x)
过程: 在训练数据集所在的输入空间中,递归地将每一个区域划分为两个子区域上的输出值,构建二叉决策树:
(1) 选择最优化切分特征jjj与阈值sss,
求解以下最优化:
argj,smin∑m=12∑xi∈Rm(j,s)(yi−cm)2\arg_{j,s} \min \sum_{m=1}^2\sum_{\boldsymbol{x}_i\in R_m(j,s)}(y_i-c_m)^2argj,sminm=1∑2xi∈Rm(j,s)∑(yi−cm)2
R1(j,s)={(xi,yi)∣yi≥s} R_1(j,s)=\{(\boldsymbol{x}_i,y_i)|y_i\ge s\} R1(j,s)={(xi,yi)∣yi≥s}
R2(j,s)={(xi∣yi)≤s} R_2(j,s)=\{(\boldsymbol{x}_i|y_i)\leq s\} R2(j,s)={(xi∣yi)≤s}
其中,Rm(j,s)R_m(j,s)Rm(j,s)是基于切分特征jjj与阈值sss的两个切分区域,m=1m=1m=1时,取正类;m=2m=2m=2时,取反类。NmN_mNm为切分区域后的样本总数。
cmc_mcm由最小二乘参数估计得到:
cm=1Nm∑xi∈Rm(j,s)yi(xi)c_m=\frac{1}{N_m}\sum_{\boldsymbol{x}_i\in R_m(j,s)}y_i(\boldsymbol{x_i})cm=Nm1xi∈Rm(j,s)∑yi(xi)
(2) 继续对两个子区域调用步骤(1),直至满足停止条件.
(3) 最终得到MMM个区域记为RM,m=1,2,3,...R_M,m=1,2,3,...RM,m=1,2,3,...,输出决策树:
f(x)=∑RMcMI(x∈RM)f(\boldsymbol{x})=\sum_{R_M}c_M\mathbb{I}(\boldsymbol{x}\in R_M)f(x)=RM∑cMI(x∈RM)
一个回归实例:房价预测
假设我们有以下数据集,包含3个特征(面积、房间数、楼龄)和对应的房价(万元):
| 样本 | 面积(㎡) | 房间数 | 楼龄(年) | 房价(万元) |
|---|---|---|---|---|
| 1 | 80 | 2 | 10 | 150 |
| 2 | 120 | 3 | 5 | 280 |
| 3 | 60 | 1 | 15 | 100 |
| 4 | 150 | 4 | 3 | 400 |
| 5 | 90 | 2 | 8 | 190 |
| 6 | 110 | 3 | 6 | 260 |
| 7 | 70 | 2 | 12 | 130 |
| 8 | 130 | 3 | 4 | 320 |
第一步:寻找最优切分
需遍历所有特征(面积、房间数、楼龄 )及可能阈值,计算平方误差,选误差最小的划分。
以**“面积”特征**,尝试阈值s=100m2s = 100\mathrm{m}^2s=100m2为例:
区域R1R_1R1(面积≥100):包含样本2、4、6、8
- 输出值 c1c_1c1(最小二乘估计,即样本均值 ):
c1=280+400+260+3204=12604=315c_1 = \frac{280 + 400 + 260 + 320}{4} = \frac{1260}{4} = 315c1=4280+400+260+320=41260=315 - 平方误差:
(280−315)2+(400−315)2+(260−315)2+(320−315)2=1225+7225+3025+25=1150(280 - 315)^2 + (400 - 315)^2 + (260 - 315)^2 + (320 - 315)^2 = 1225 + 7225 + 3025 + 25 = 1150(280−315)2+(400−315)2+(260−315)2+(320−315)2=1225+7225+3025+25=1150
- 输出值 c1c_1c1(最小二乘估计,即样本均值 ):
区域 R2R_2R2(面积<100):包含样本1、3、5、7
- 输出值 c2c_2c2:
c2=150+100+190+1304=5704=142.5 c_2 = \frac{150 + 100 + 190 + 130}{4} = \frac{570}{4} = 142.5 c2=4150+100+190+130=4570=142.5 - 平方误差:
(150−142.5)2+(100−142.5)2+(190−142.5)2+(130−142.5)2=56.25+1806.25+2256.25+156.25=4275 (150 - 142.5)^2 + (100 - 142.5)^2 + (190 - 142.5)^2 + (130 - 142.5)^2 = 56.25 + 1806.25 + 2256.25 + 156.25 = 4275 (150−142.5)2+(100−142.5)2+(190−142.5)2+(130−142.5)2=56.25+1806.25+2256.25+156.25=4275
- 输出值 c2c_2c2:
总误差:11500+4275=1577511500 + 4275 = 1577511500+4275=15775
经遍历所有可能,“面积=100㎡”划分的总误差最小,根节点确定为“面积≥100?”
(二)递归划分
对首次划分得到的两个子区域,继续递归划分,直到满足停止条件(此处设定“叶子节点样本数≤1时停止” )。
1. 对 R1R_1R1(面积≥100)划分
尝试**“房间数”特征**,阈值 s=3s = 3s=3:
- 区域 R11R_{11}R11(面积≥100且房间数≥3):包含样本2、4、6、8
- 输出值 c11=280+400+260+3204=315c_{11} = \frac{280 + 400 + 260 + 320}{4} = 315c11=4280+400+260+320=315
- 平方误差:115001150011500(同首次划分 R1R_1R1 )
- 区域 R12R_{12}R12(面积≥100且房间数<3):无样本(面积大的房子房间数均≥3 )
2. 对 R2R_2R2(面积<100)划分
尝试**“楼龄”特征**,阈值 s=10s = 10s=10:
- 区域 R21R_{21}R21(面积<100且楼龄≥10):包含样本1、3、7
- 输出值 c21c_{21}c21:
c21=150+100+1303≈126.67 c_{21} = \frac{150 + 100 + 130}{3} \approx 126.67 c21=3150+100+130≈126.67 - 平方误差:
(150−126.67)2+(100−126.67)2+(130−126.67)2≈544.44+711.11+11.11=1266.66 (150 - 126.67)^2 + (100 - 126.67)^2 + (130 - 126.67)^2 \approx 544.44 + 711.11 + 11.11 = 1266.66 (150−126.67)2+(100−126.67)2+(130−126.67)2≈544.44+711.11+11.11=1266.66
- 输出值 c21c_{21}c21:
- 区域 R22R_{22}R22(面积<100且楼龄<10):包含样本5
- 输出值 c22=190c_{22} = 190c22=190(仅1个样本,输出值为该样本房价 )
- 平方误差:000(单个样本无误差 )
因 R22R_{22}R22 样本数为1,满足“叶子节点样本数≤1”的停止条件,递归结束。
(三)最终回归树结构
根节点:面积≥100?
├─ 是 → 输出315
└─ 否 → 楼龄≥10?
├─ 是 → 输出126.67
└─ 否 → 输出190
三、预测示例
新样本:(面积=95㎡, 房间数=2, 楼龄=9年)
- 面积95 < 100 → 进入“否”分支(楼龄≥10? )
- 楼龄9 < 10 → 进入“否”分支
- 输出值为 190190190 万元
四、实际应用说明
实际场景中,划分会更复杂:
- 需遍历更多特征、更多阈值,找全局最优划分;
- 停止条件更丰富(如限制树的最大深度、设定最小样本划分数量、设置平方误差下降阈值等 ),避免过拟合或欠拟合。
此示例简化演示了回归树“递归划分特征空间 + 局部均值预测”的核心逻辑,帮助理解其工作原理。