初识无监督学习-聚类算法中的K-Means算法，从原理公式到简单代码实现再到算法优化

无监督学习

聚类算法

与分类算法区别：分类算法仍是监督学习的范畴，样本数据除了特征，还带有标签；而聚类算法是一种无监督学习算法，样本数据只有特征没有标签

查看数据集中所有数据，在数据集中找到彼此相似数据组，就称为聚类

K-Means 算法

算法描述

K-Means存储用于定义聚类的 k 个质心。如果一个点离哪个质心最接近，则该点被视为位于哪个聚类中

K-Means的目标是**最小化簇内平方误差和 WCSS**：每个点到其所属簇质心的距离的平方和
$$\begin{gathered} WCSS=\sum _{i=1}^K\sum _{x\in c^{(i)}}||x-{\mu }_i|{|}^2 \\ K:簇的数量 \\ {c}^{(i)}:第i个簇(类别)的点集 \\ {\mu }_i:第i个簇(类别)的质心 \end{gathered}$$
K-Means接受参数k，将事先输入的n个对象划分为k个聚类，以便使所获得的聚类满足：

• 同一聚类中的对象相似度较高
• 不同聚类中的对象相似度较小

K-Means通过交替进行下面两步来找到最佳质心：

• 根据当前质心将数据点划分到某聚类中
• 根据当前数据点计算聚类的质心

算法思想

以空间中k个点为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心的值，直至得到最好的聚类结果

算法步骤

1. 初始化 k 个聚类的质心μ

   1. $${\mu }_1,{\mu }_2,\dots ,{\mu }_k\in R^n$$

2. 重复以下两步，迭代直到收敛

4. 对于每个数据点 xi，找到距离最近的质心对应的类别

   • $$\begin{gathered} c^{(i)}=argmi{n}_j||x^{(i)}-{\mu }_j|{|}^2 \\ argmi{n}_{arg}(exp)是找到使exp最小的arg \\ 即c^{(i)}是使|x^{(i)}-{\mu }_j{|}^2最小的j \end{gathered}$$

   • ​

5. 对每个类别 j，根据这个类别中数据的平均值计算得到新的质心

   • μj:=∑i=1m1{c(i)=j}x(i)∑i=1m1{c(i)=j} \mu_j := \frac{\sum_{i=1}^{m}1\{{c^{(i)}=j\}}x^{(i)}}{\sum_{i=1}^{m}1\{{c^{(i)}=j\}}} μj​:=∑i=1m​1{c(i)=j}∑i=1m​1{c(i)=j}x(i)​

   • 

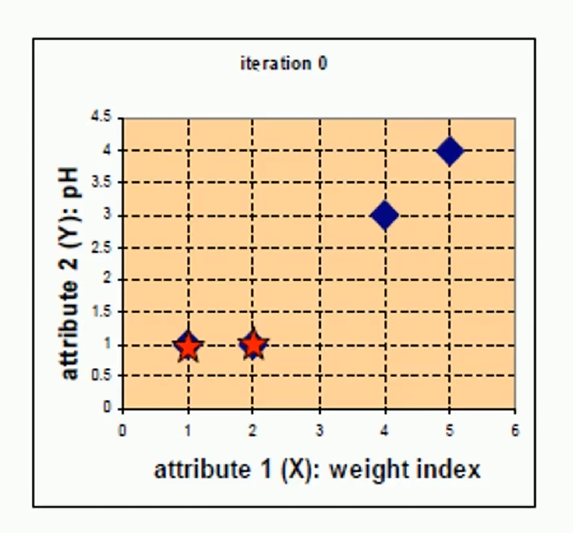
比如上面这张图

点集为[(1,1),(2,1),(4,3),(5,4)] = [A,B,C,D]

选取质心为(1,1),(2,1),那么所有点到质心的距离为

[0.         1.         3.60555128 5.        ] -- group-1
[1.         0.         2.82842712 4.24264069] -- group-2

使用one-hot表示这一轮后的点的分类

[1 0 0 0]
[0 1 1 1]
 A B C D

为什么这个矩阵一开始看起来这么诡异?

因为使用one-hot编码表示属于哪个质心对应的类别

更新质心

(1,1)对应的类别c1中，还是只有质心一个数据对象，不用更新

(2,1)对应的类别c2中，新增了2个数据对象，更新
$${\mu }_2=(\frac{2+4+5}{3},\frac{1+3+4}{3})=(\frac{11}{3},\frac{8}{3})$$
迭代上述过程，直到聚类不发生变化

代码实现

导入数据，使用sklearn.datasets.make_blobs()生成聚类数据

from sklearn.datasets import make_blobs

# 100个样本,5个聚类中心
X, y = make_blobs(n_samples=100, centers=5)

点图

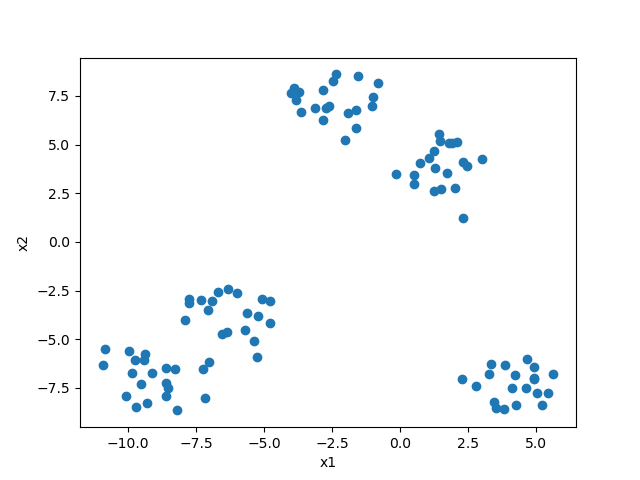
初始化质心

# 初始化质心
def init_centroid(X, k):
        sample_size, f_size = X.shape
        # k个质心的集合
        centroids = np.zeros((k, f_size))

        for i in range(k):
                # 随机索引
                index = int(np.random.uniform(low=0, high=sample_size))
                # 抽到的点加入质心集合
                centroids[i, :] = X[index, :]

        return centroids

K-Means

def kmeans(X, k):
        sample_size = X.shape[0]
        # 初始化质心
        centroids = init_centroid(X, k)
        # cluster_data[:,0]表示数据点所属的簇,cluster_data[:,1]表示数据点到簇质心的距离
        cluster_data = np.zeros((sample_size, 2))
        # 当簇是否更新的标志
        flag = True

        while flag:
                flag = False
                for i in range(sample_size):
                        # 最小距离
                        min_dist = np.inf
                        # 最近质心的索引
                        min_index = -1
                        for j in range(k):
                                diff = X[i, :] - centroids[j, :]
                                # print(f"diff.shape={diff.shape}")
                                dist = np.sqrt(np.sum(diff ** 2))
                                # print(f"dist={dist}")

                                # 更新与附近质心的最近距离
                                if dist < min_dist:
                                        min_dist = dist
                                        cluster_data[i][1] = dist
                                        min_index = j

                        # 聚类发生变化
                        if cluster_data[i][0] != min_index:
                                flag = True
                                cluster_data[i][0] = min_index

                for j in range(k):
                        # 类别为j的索引
                        index = np.nonzero(cluster_data[:, 0] == j)
                        # 所有类别为j的数据对象
                        data = X[index]
                        # 更新质心
                        centroids[j, :] = np.mean(data, axis=0)

        return centroids, cluster_data

绘制聚类图

def show(X, centroids, cluster_data, k):
        sample_size = X.shape[0]
        # 红色圆点，蓝色圆点，绿色圆点，黄色圆点
        mark = ['or', 'ob', 'og', 'oy']
        # 红色星星，蓝色星星，绿色星星，黄色星星
        m = ['*r', '*b', '*g', '*y']
        for i in range(sample_size):
                # 获取所属的簇
                index = int(cluster_data[i, 0])
                plt.plot(X[i, 0], X[i, 1], mark[index])

        for i in range(k):
                plt.plot(centroids[i, 0], centroids[i, 1], m[i], markersize=20)
        plt.show()

全部代码

import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobs


def plot_point(X):
        plt.scatter(X[:, 0], X[:, 1])
        plt.xlabel("x1")
        plt.ylabel("x2")
        plt.show()


# 初始化质心
def init_centroid(X, k):
        sample_size, f_size = X.shape
        # k个质心的集合
        centroids = np.zeros((k, f_size))

        for i in range(k):
                # 随机索引
                index = int(np.random.uniform(low=0, high=sample_size))
                # 抽到的点加入质心集合
                centroids[i, :] = X[index, :]

        return centroids


def kmeans(X, k):
        sample_size = X.shape[0]
        # 初始化质心
        centroids = init_centroid(X, k)
        # cluster_data[:,0]表示数据点所属的簇,cluster_data[:,1]表示数据点到簇质心的距离
        cluster_data = np.zeros((sample_size, 2))
        # 当簇是否更新的标志
        flag = True

        while flag:
                flag = False
                for i in range(sample_size):
                        # 最小距离
                        min_dist = np.inf
                        # 最近质心的索引
                        min_index = -1
                        for j in range(k):
                                diff = X[i, :] - centroids[j, :]
                                # print(f"diff.shape={diff.shape}")
                                dist = np.sqrt(np.sum(diff ** 2))
                                # print(f"dist={dist}")

                                # 更新与附近质心的最近距离
                                if dist < min_dist:
                                        min_dist = dist
                                        cluster_data[i][1] = dist
                                        min_index = j

                        # 聚类发生变化
                        if cluster_data[i][0] != min_index:
                                flag = True
                                cluster_data[i][0] = min_index

                for j in range(k):
                        # 类别为j的索引,np.nonzero()会返回布尔数组中为True的元素的索引
                        index = np.nonzero(cluster_data[:, 0] == j)
                        # 所有类别为j的数据对象
                        data = X[index]
                        # 更新质心
                        centroids[j, :] = np.mean(data, axis=0)

        return centroids, cluster_data


def show(X, centroids, cluster_data, k):
        sample_size = X.shape[0]
        # 红色圆点，蓝色圆点，绿色圆点，黄色圆点
        mark = ['or', 'ob', 'og', 'oy']
        # 红色星星，蓝色星星，绿色星星，黄色星星
        m = ['*r', '*b', '*g', '*y']
        for i in range(sample_size):
                # 获取所属的簇
                index = int(cluster_data[i, 0])
                plt.plot(X[i, 0], X[i, 1], mark[index])

        for i in range(k):
                plt.plot(centroids[i, 0], centroids[i, 1], m[i], markersize=20)
        plt.show()


# 100个样本,4个聚类中心
X, y = make_blobs(n_samples=100, centers=4, random_state=42)
k = 4
centroids, cluster_data = kmeans(X, k)

# 检验空簇
if np.isnan(centroids).any():
        print("Error")
else:
        print("Success")

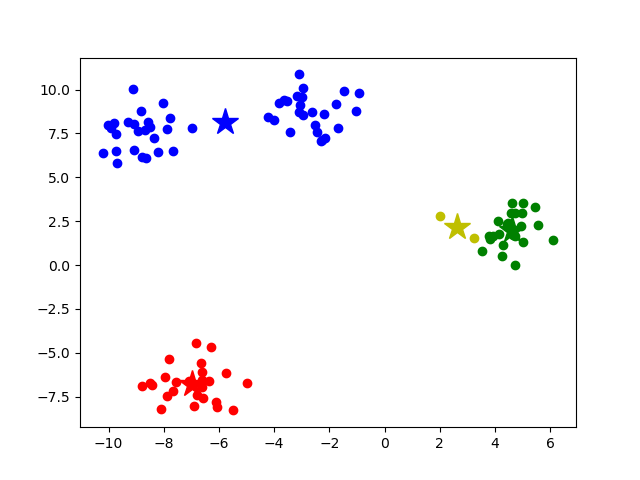
show(X, centroids, cluster_data, k)

得到的聚类图

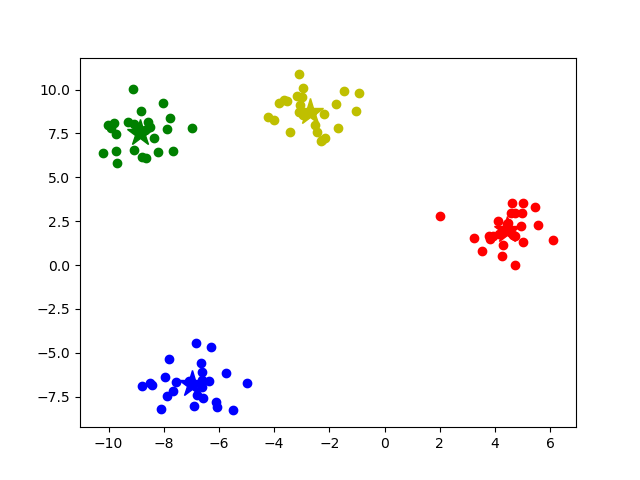
存在的问题

• 更新质心时应该是更新当前类别为j的数据对象，而不是更新所有的；传错参数最后会导致所有数据都是一个聚类
• 有时会出现簇消失的情况，最终分类的簇的个数小于我们预设的k，如图所示
  

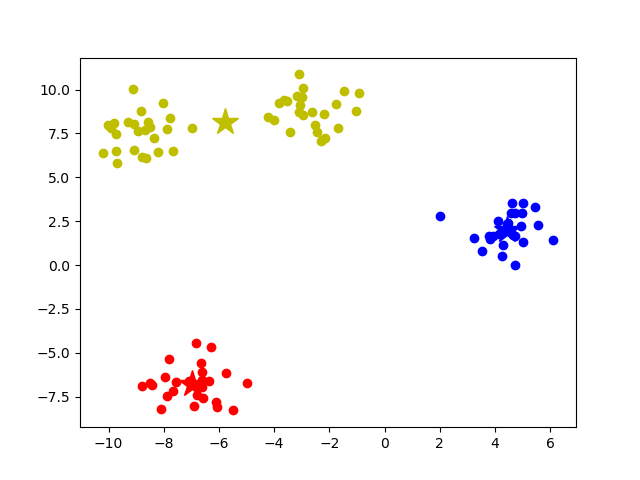
此时的质心列表

[[-6.9749469  -6.76471966]
 [ 4.44441765  2.02122148]
 [        nan         nan]
 [-5.77644235  8.14575097]]

为什么会这样呢？

因为j类簇是个空簇，所以获取j类别里元素索引列表的时候，获取的列表是空，取均值时会变成nan

出现空簇是因为:我们的质心是随机选取的，有质心重合的可能性，造成有一个质心对应的的簇变成空簇

解决:

抽取质心的时候就不让它重复

# 初始化质心:改用np.random.choice进行不充分抽样
def init_centroid(X, k):
        sample_size, f_size = X.shape

        # 从0-sample_size-1随机抽取k个不重复的数作为索引
        index = np.random.choice(sample_size, size=k, replace=False)
        centroids = X[index]

        return centroids

使用sklearn的api

基本使用

from sklearn.cluster import KMeans

数据

# 100个样本,5个聚类中心
X, y = make_blobs(n_samples=100, centers=4, random_state=42)
k = 4

模型

kmeans = KMeans(
        n_clusters=4,  # 分为k类
        init="random",  # 初始随机选取质心
        n_init=5,  # 初始质心数
        max_iter=100  # 最大迭代次数
)

拟合数据

kmeans.fit(X)

获取每个样本的聚类标签

cluster_label = kmeans.predict(X)
# 二者等价
cluster_label = kmeans.labels_

获取质心

kmeans.cluster_centers_

绘图

def fill(model, X, labels):
        X_min, X_max = X[:, 0].min(), X[:, 0].max()
        y_min, y_max = X[:, 1].min(), X[:, 1].max()

        # 创建网格
        xx, yy = np.meshgrid(
                np.arange(X_min, X_max, 0.02),
                np.arange(y_min, y_max, 0.02),
        )

        # np.c_[]表示按列拼接,比如[1,2,3]和[4,5,6]拼接后变成[[1,4],[2,5],[3,6]]
        # .ravel()和.flatten()都是将多维数组展平,但是.flatten返回的是副本,.ravel()返回视图
        z = model.predict(np.c_[xx.ravel(), yy.ravel()])
        # 模型预测结果是1D,升维
        z = z.reshape(xx.shape)
        # 绘制填充等高线
        cs = plt.contourf(xx, yy, z)

        data_size = X.shape[0]
        # 红色圆点，蓝色圆点，绿色圆点，黄色圆点
        mark = ['or', 'ob', 'og', 'oy']
        for i in range(data_size):
                plt.plot(X[i, 0], X[i, 1], mark[labels[i]], alpha=0.3)

        for i in range(k):
                plt.plot(centers[i, 0], centers[i, 1], '*w', markersize=20)

        plt.show()

最终聚类结果图

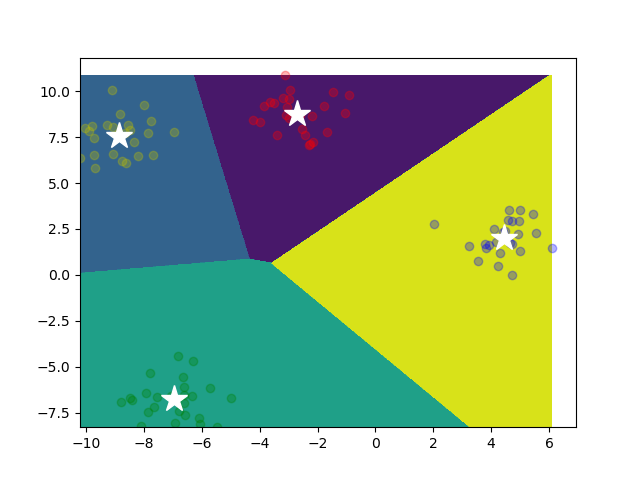
Mini Batch K-Means

Mini Batch K-Means是K-Means的一个变种；采用小批量的数据子集迭代更新聚类中心。小批量指的是每次训练算法时所随机抽取的数据子集

优点

• 只是用数据的一个小批量，计算量减少了，收敛速度加快
• 聚类结果与标准K-Means相近，但是速度更快

迭代步骤

• 从数据集中随机抽取一些数据形成小批量，把他们分配给最近的质心
• 更新质心，与K-Means相比，Mini Batch K-Means是在更小的样本集上更新

sklearn-api

from sklearn.cluster import MiniBatchKMeans
mini_batch_kmeans = MiniBatchKMeans(n_clusters=4)

KMeans缺点

• 对初始质心的选择较敏感

• k值选取是由用户决定，k不一定最优

  k太大

  

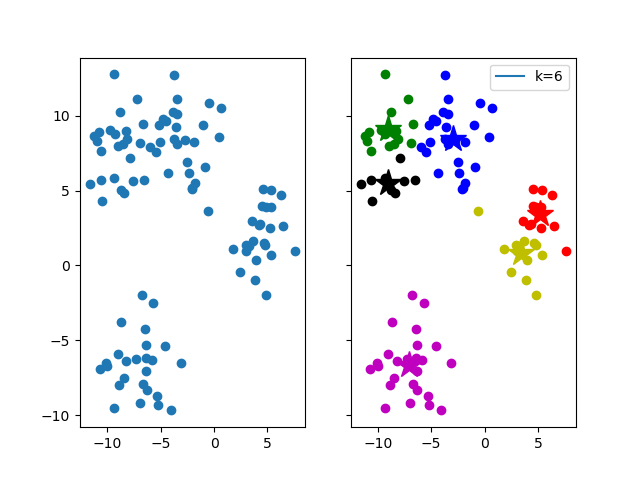
  有不必要的划分

  k太小

  

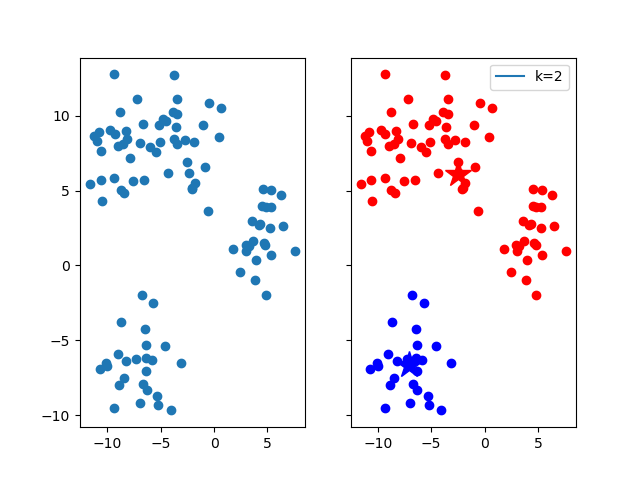
  没有完全区分开聚类

• 不适合非球型簇，K-means 假设每个簇是球形且大小相近

  用月牙形数据进行验证

  from sklearn.datasets import make_moons
  X, y = make_moons(n_samples=100, noise=0.05, random_state=42)
  

  原数据点与聚类结果，我们预想的应该是：每个月牙形是一个聚类

  

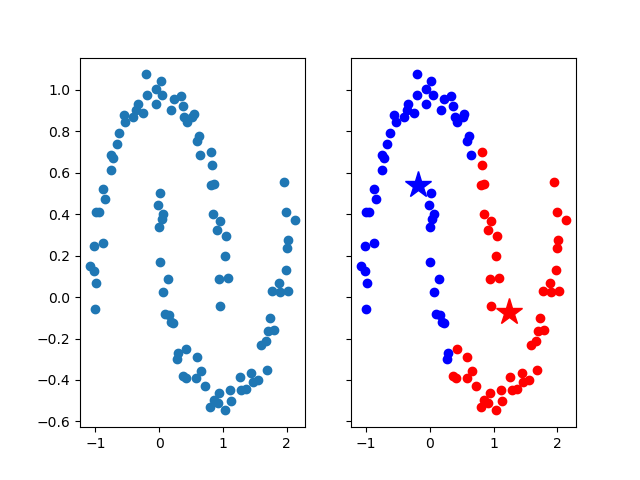
  但是实际上并没有，K-Means的搜索逻辑就是按距离搜索，所以聚类的形状会趋近于球型

• 容易陷入局部最优

  如图所示，确实是收敛了，但是只是收敛到了局部最小值

  

• 算法要求样本存在均值(为了更新质心)，限制了数据的种类

• 对噪声敏感

  使用cluster_std指定高斯分布簇的松散程度，相当于引入噪音

  X, y = make_blobs(
          n_samples=100,
          centers=4,
          random_state=42,
          cluster_std=10  # 控制松散程度，越大越松散，相当于引入噪音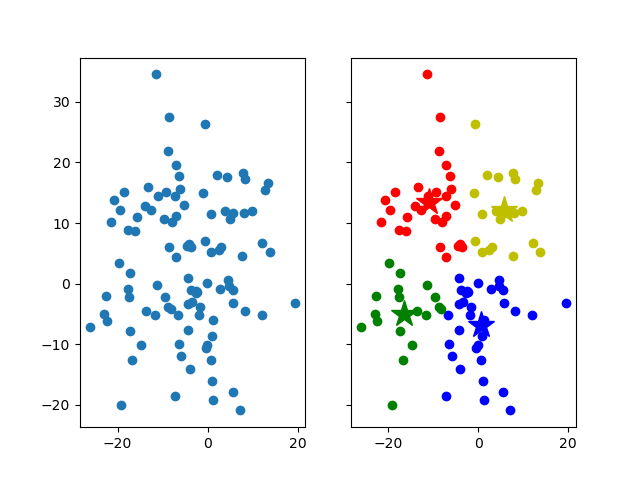
  )
  

  

K-Means优化

对初始质心的选择

使用多次的随机初始化，计算每一次建模得到的代价函数的值，选取代价函数最小的结果作为聚类结果

代价函数/簇内平方误差和WCSS

$$\begin{gathered} WCSS=\sum _{i=1}^K\sum _{x\in c^{(i)}}||x-{\mu }_i|{|}^2 \\ K:簇的数量 \\ {c}^{(i)}:第i个簇(类别)的点集 \\ {\mu }_i:第i个簇(类别)的质心 \\ ||||表示取模操作，方便将算法向量化 \end{gathered}$$

代码实现

循环:

K-Mean利用最开始的手动实现

def cost(cluster_data, X, centers):
        k = centers.shape[0]
        loss = 0
        for j in range(k):
                index = np.nonzero(cluster_data[:, 0] == j)
                cluster = X[index]
                diff = cluster - centers[j]
                loss += (np.sum(diff ** 2))

        return loss

使用向量化进行优化

模型使用sklearn的api

def WCSS(X, labels, centers):
        # 获取每个点对应的质心
        # 利用numpy的整数索引,相当于assigned_centers[i]=centers[labels[i]],shape=(labels.shape[0],centers.shape[1])
        assigned_centers = centers[labels]
        diff = X - assigned_centers

        return np.sum(diff ** 2)

模型

# 100个样本,5个聚类中心
X, y = make_blobs(
        n_samples=100,
        centers=4,
        random_state=42,
        cluster_std=2  # 控制松散程度，越大越松散，相当于引入噪音
)

k = 4

kmeans = KMeans(n_clusters=k)
kmeans.fit(X)
labels = kmeans.labels_
centers = kmeans.cluster_centers_

选出最优质心

改进后的KMeans

def kmeans(X, k, iters=100):
        '''
        
        :param X: 数据
        :param k: 最终分出的聚类数
        :param iters: 迭代多少次找到最优质心
        :return: 
        '''
        sample_size = X.shape[0]
        best_centers = np.zeros((k, 2))
        best_cluster_data = np.zeros((k, 2))
        best_wcss = np.inf

        for _ in range(iters):
                # 当簇是否更新的标志
                flag = True
                
                # 初始化质心
                centroids = init_centroid(X, k)
                # cluster_data[:,0]表示数据点所属的簇,cluster_data[:,1]表示数据点到簇质心的距离
                cluster_data = np.zeros((sample_size, 2))
                while flag:
                        flag = False
                        for i in range(sample_size):
                                # 最小距离
                                min_dist = np.inf
                                # 最近质心的索引
                                min_index = -1
                                for j in range(k):
                                        diff = X[i, :] - centroids[j, :]
                                        # print(f"diff.shape={diff.shape}")
                                        dist = np.sqrt(np.sum(diff ** 2))
                                        # print(f"dist={dist}")

                                        # 更新与附近质心的最近距离
                                        if dist < min_dist:
                                                min_dist = dist
                                                cluster_data[i][1] = dist
                                                min_index = j

                                # 聚类发生变化
                                if cluster_data[i][0] != min_index:
                                        flag = True
                                        cluster_data[i][0] = min_index

                        for j in range(k):
                                # 类别为j的索引
                                index = np.nonzero(cluster_data[:, 0] == j)
                                # 所有类别为j的数据对象
                                if len(index) > 0:
                                        data = X[index]
                                        # 更新质心
                                        centroids[j, :] = np.mean(data, axis=0)
                                else:
                                        print("空簇")
                wcss = cost(cluster_data, X, centroids)
                if wcss < best_wcss:
                        best_wcss = wcss
                        best_centers = centroids
                        best_cluster_data = cluster_data
        return best_centers, best_cluster_data


def show(X, centroids, cluster_data, ax, k):
        sample_size = X.shape[0]
        # 圆点（circle）
        mark = ['or', 'ob', 'og', 'oy', 'ok', 'om', 'oc']  # 红、蓝、绿、黄、黑、品红、青

        # 星星（star）
        m = ['*r', '*b', '*g', '*y', '*k', '*m', '*c']
        for i in range(sample_size):
                # 获取所属的簇
                index = int(cluster_data[i, 0])
                ax.plot(X[i, 0], X[i, 1], mark[index])

        for i in range(k):
                ax.plot(centroids[i, 0], centroids[i, 1], m[i], markersize=20)

        ax.plot([], [], label=f"k={k}")
        plt.legend()
        plt.show()


def cost(cluster_data, X, centers):
        k = centers.shape[0]
        loss = 0
        for j in range(k):
                index = np.nonzero(cluster_data[:, 0] == j)
                cluster = X[index]
                diff = cluster - centers[j]
                loss += (np.sum(diff ** 2))

        return loss

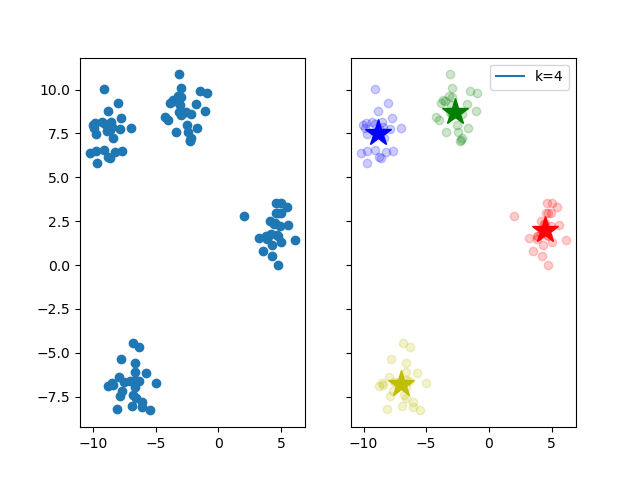
最终聚类图

K-Means++

核心思想

让每个新的聚类中心尽可能远离已选的聚类中心

算法流程

1. 随机选取一个聚类中心μ1，从数据集中随机选取一个点
2. 对第i个聚类中心(i=2,…,k)

• 计算每个样本x到当前已选的所有聚类中心的最短距离D(x)
  $$\begin{gathered} D(x)=\underset{{\mu }_1,\dots ,{\mu }_{i-1}}{\min }||x-{\mu }_j|| \\ j=1,\dots ,i-1 \end{gathered}$$

• 按照概率P(x)选择下一个聚类中心
  $$P(x)=\frac{D(x{)}^2}{{\sum }_{x}D(x{)}^2}$$
  并不是选取概率最大的，而是按照概率分布选择(?)

  • 得到每个点的概率之后，我们需要计算累积概率，比如概率分布[0.1,0.2,0.7],累积概率分布为[0.1,0.3,1.0]
  • 生成一个[0,1]之间的随机数r
  • 找到第一个累积概率大于等于r的点作为下一个质心

3.一旦所有 k 个初始聚类中心选定，后续步骤与标准 K-Means 相同

sklearn中使用K-Means++

init属性默认使用k-means++；也可以构建K-Means模型时显式指定init属性为k-means++

kmeans = KMeans(
        n_clusters=k,  # 分为k类
        init="k-means++",  # 使用k-means++选取质心
        n_init=5,  # 初始质心数
        max_iter=100  # 最大迭代次数
)

手动实现

def get_min_dists(X, centers):
        '''
        
        :param X: 数据
        :param centers: 当前的所有质心
        :return: 所有样本点与其最近的质心的距离
        '''
        sample_size = X.shape[0]
        min_dists = np.zeros(sample_size)

        for i in range(sample_size):
                min_dist = np.inf
                for center in centers:
                        dist = np.sum((X[i] - center) ** 2)
                        if dist < min_dist:
                                min_dist = dist
                min_dists[i] = min_dist

        return min_dists


def kmeans_pp(X, k):
        sample_size, _ = X.shape
        centers = []

        # 随机选择第一个中心点
        first_idx = np.random.choice(sample_size, size=1)[0]
        centers.append(X[first_idx])

        for _ in range(k - 1):
                dists = get_min_dists(X, centers)

                # 构建概率分布
                probs = dists / dists.sum()
                # 计算累计和
                cum_probs = np.cumsum(probs)
                
                # 使用转盘法
                # 生成一个 [0,1] 之间的随机数
                r = np.random.rand()
                # 找到第一个累积概率大于等于 r 的样本点
                for i in range(sample_size):
                        if cum_probs[i] >= r:
                                centers.append(X[i])
                                break

        return np.array(centers)

K值选取

肘部法则

绘制不同k值下WCSS的图像，寻找"肘部"点作为最佳K值

核心思想

随着k值的增大，聚类的误差会不断减小，但当k增大到某个值之后，误差下降的幅度会显著变小，形成一个肘部形状的拐点

绘图代码

K-Means使用前面对选取初始质心优化后的代码

def manba(Ks):
        X, y = make_blobs(n_samples=300, centers=4, random_state=42)

        wcss = []

        for k in Ks:
                centroids, cluster_data = kmeans(X, k, iters=10)
                current_wcss = cost(cluster_data, X, centroids)
                wcss.append(current_wcss)

        plt.figure(figsize=(8, 5))
        plt.plot(Ks, wcss, 'bo-', linewidth=2, markersize=8)
        plt.title('Elbow Method for Optimal k')
        plt.xlabel('Number of clusters (k)')
        plt.ylabel('Within-Cluster Sum of Squares (WCSS)')
        plt.grid(True)
        # 用k的取值作为横轴刻度
        plt.xticks(Ks)
        plt.show()

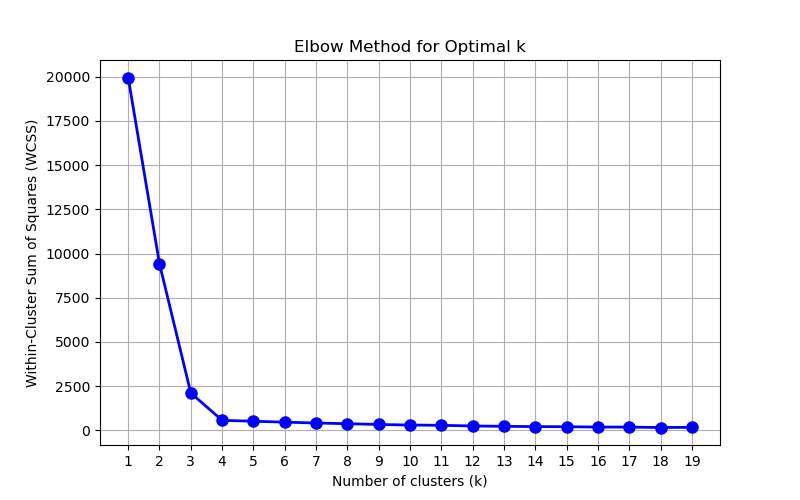
由图中我们可以看到k=4是拐点，而我们创建的数据集设置簇为4，所以最终聚类聚成4个类最合适

缺点:主观性较强，尤其是如果肘部不明显

轮廓系数

用于衡量聚类结果中每个样本的“聚类合理性”,即该样本是否被正确分配到正确的簇中

对于每个样本点i，其轮廓系数s(i)的计算公式如下:
s(i)=b(i)−a(i)max{a(i),b(i)}a(i):样本点i到同簇其他点的平均距离b(i):样本点i到最近其他簇中所有点的平均距离 s(i)= \frac{b(i)-a(i)}{max\{a(i),b(i)\}} \\ a(i):样本点i到同簇其他点的平均距离\\ b(i):样本点i到最近其他簇中所有点的平均距离\\ s(i)=max{a(i),b(i)}b(i)−a(i)​a(i):样本点i到同簇其他点的平均距离b(i):样本点i到最近其他簇中所有点的平均距离
轮廓系数的取值范围位于[-1,1]

• -1:样本点可能错误地被分配到了其他簇
• 0:样本点位于两个簇之间
• 1:样本点被聚类得很好

使用sklearn实现

# 计算整体轮廓系数和单个样本轮廓系数
from sklearn.metrics import silhouette_score,silhouette_samples

寻找最优的k:轮廓系数最大对应的k

def get_best_K(Ks):
        X, y = make_blobs(
                n_samples=100,
                centers=4,
                random_state=42,
        )
        plt.scatter(X[:, 0], X[:, 1], c='b')
        scores = []

        for k in Ks:
                kmeans = KMeans(n_clusters=k)
                kmeans.fit(X)
                labels = kmeans.labels_
                score = silhouette_score(X, labels)
                print(score)
                scores.append(score)

        plt.figure(figsize=(8, 5))
        plt.plot(Ks, scores, 'bo-', linewidth=2, markersize=8)
        plt.xlabel('Number of clusters (k)')
        plt.ylabel('silhouette_score')
        plt.grid(True)
        # 用k的取值作为横轴刻度
        plt.xticks(Ks)
        plt.show()

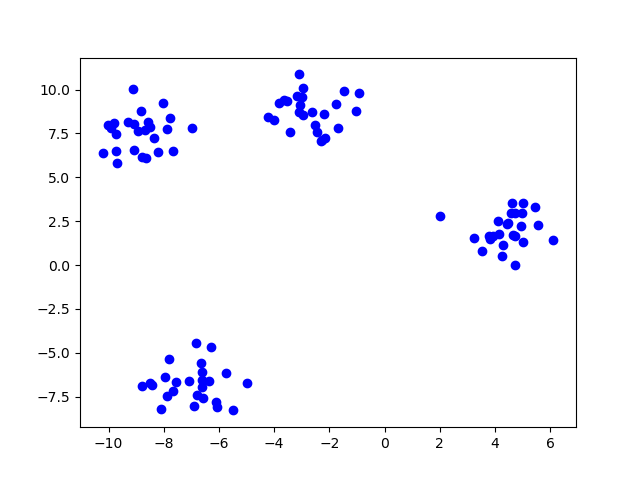
样本点图

绘制的整体轮廓系数与k的关系曲线

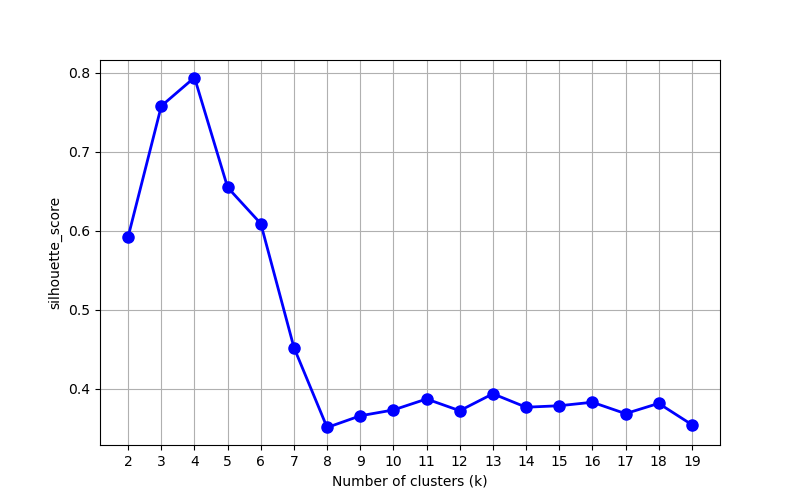
可以看到当k=4时，整体轮廓系数最大，也就是说，分成4簇是最优的

Calinski-Harabasz 指数/方差比准则

核心思想:簇间离散度越大越好，簇内离散度越小越好

直观上理解就是每个簇内部抱得很紧，外部与其他簇保持距离，形成很鲜明的聚类
$$\begin{gathered} CH=\frac{B(k)}{W(k)}\times \frac{N-k}{k-1} \\ B(k):簇间离散度 \\ B(k)=\sum _{i=1}^k{n}_i||{\mu }_i-\mu |{|}^2 \\ {n}_i:第i个簇的样本数 \\ {\mu }_i:第i个簇的中心 \\ \mu :整个数据集的均值向量 \\ W(k):簇内离散度 \\ W(k)=WCSS=\sum _{i=1}^k\sum _{x\in c^{(i)}}||x-{\mu }_i|{|}^2 \\ N:样本总数 \\ k:簇的数量 \end{gathered}$$

sklearn实现

from sklearn.metrics import calinski_harabasz_score as CH

选择最优k并绘制CH与k的关系曲线

def get_best_K_by_CH(Ks):
        X, y = make_blobs(
                n_samples=100,
                centers=4,
                random_state=42,
        )
        plt.scatter(X[:, 0], X[:, 1], c='b')
        scores = []
        max_score = -1
        best_k = 0
        for k in Ks:
                kmeans = KMeans(n_clusters=k)
                kmeans.fit(X)
                labels = kmeans.labels_
                score = CH(X, labels)
                print(score)

                if score > max_score:
                        max_score = score
                        best_k = k
                scores.append(score)

        plt.figure(figsize=(8, 5))
        plt.plot(Ks, scores, 'bo-', linewidth=2, markersize=8)
        plt.xlabel('Number of clusters (k)')
        plt.ylabel('CH')
        plt.grid(True)
        # 用k的取值作为横轴刻度
        plt.xticks(Ks)
        plt.show()
        return best_k

得到的CH与k的关系曲线

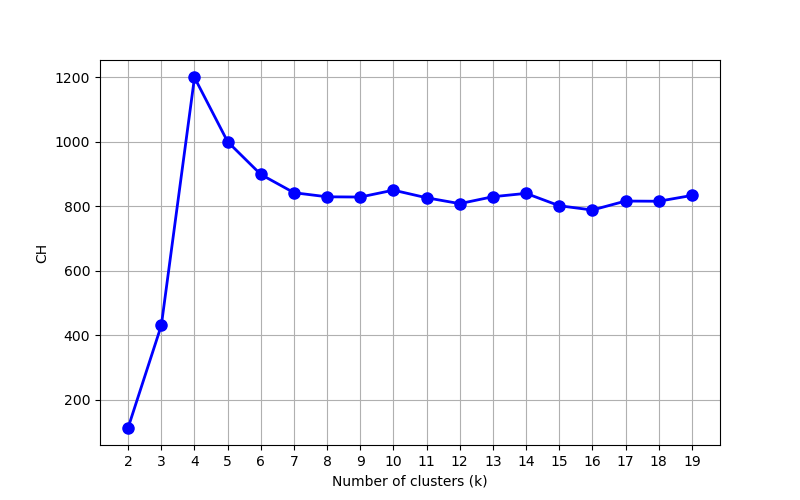
最优k为4