【数据结构初阶】--二叉树（三）-EW帮帮网

😘个人主页：@Cx330❀

👀个人简介：一个正在努力奋斗逆天改命的二本觉悟生

📖个人专栏：《C语言》《LeetCode刷题集》《数据结构-初阶》

前言：上篇博客中我们完成了堆结构的实现和堆排序的实现，在实现堆排序中，我们使用了向下调整算法建堆，那能不能用向上调整算法建堆呢？这篇博客讲给大家，并且再给大家讲解一个经典问题Top-K问题

一.向上调整算法建堆和向下调整算法建堆的时间复杂度计算

二.向上调整算法建堆和向下调整算法建堆的时间复杂度对比以及堆排序的时间复杂度

一.向上调整算法建堆和向下调整算法建堆的时间复杂度计算

首先我们看一下向上调整算法建堆（向下调整算法建堆在上篇博客里）

//向上调整算法建堆
for (int i = 0; i < n; i++)
{
	AdjustUp(arr, i);
}

本质就是从第一个节点开始，依次向下使用向上调整算法建堆

那向上和向下调整算法都可以建堆，那我们使用哪个呢？当然是哪个“好”用哪个，那这里的“好”，显然易见要算时间复杂度啦

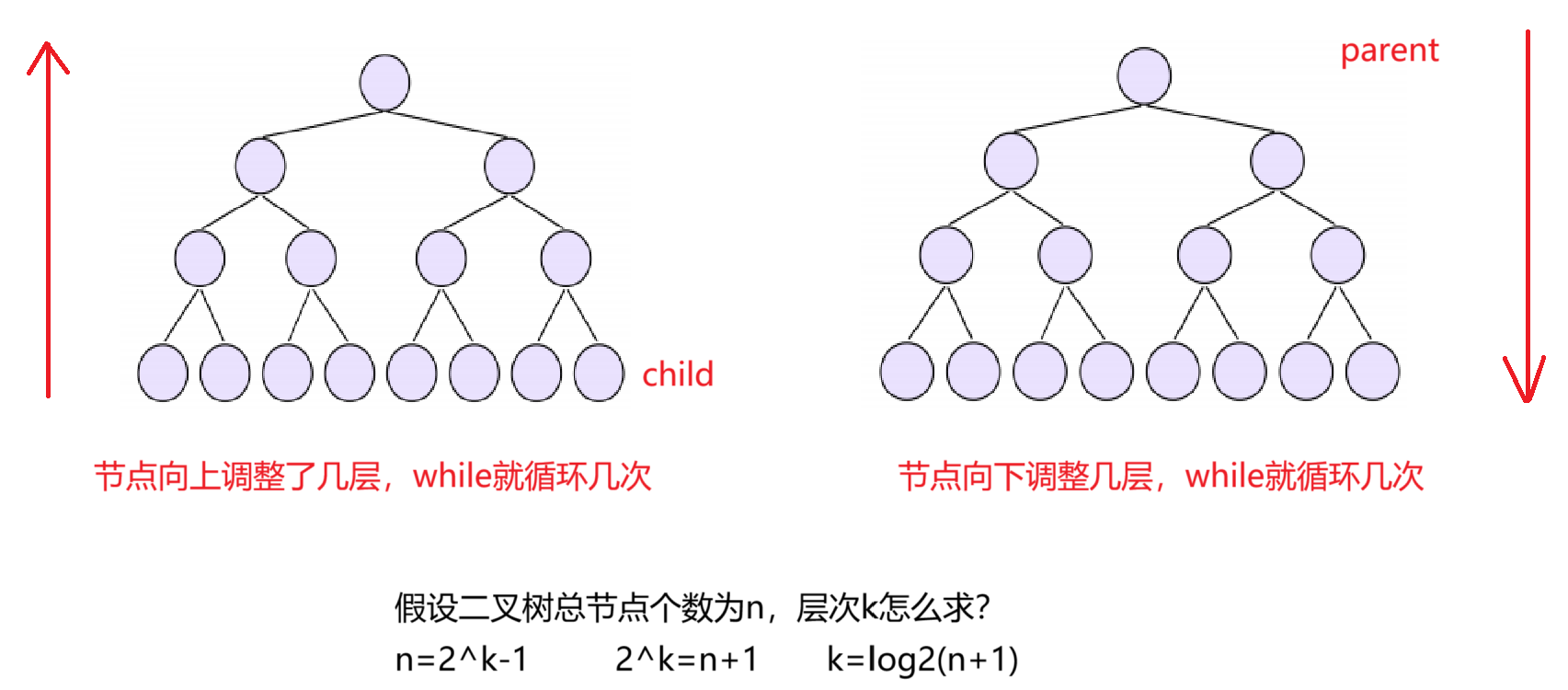
我们来看一下向上调整算法和向下调整算法的时间复杂度

如图所示我们可知向上调整算法和向下调整算法的时间复杂度都是O(logn)

那么我们来看一下向上/下建堆的时间复杂度是否相同呢？

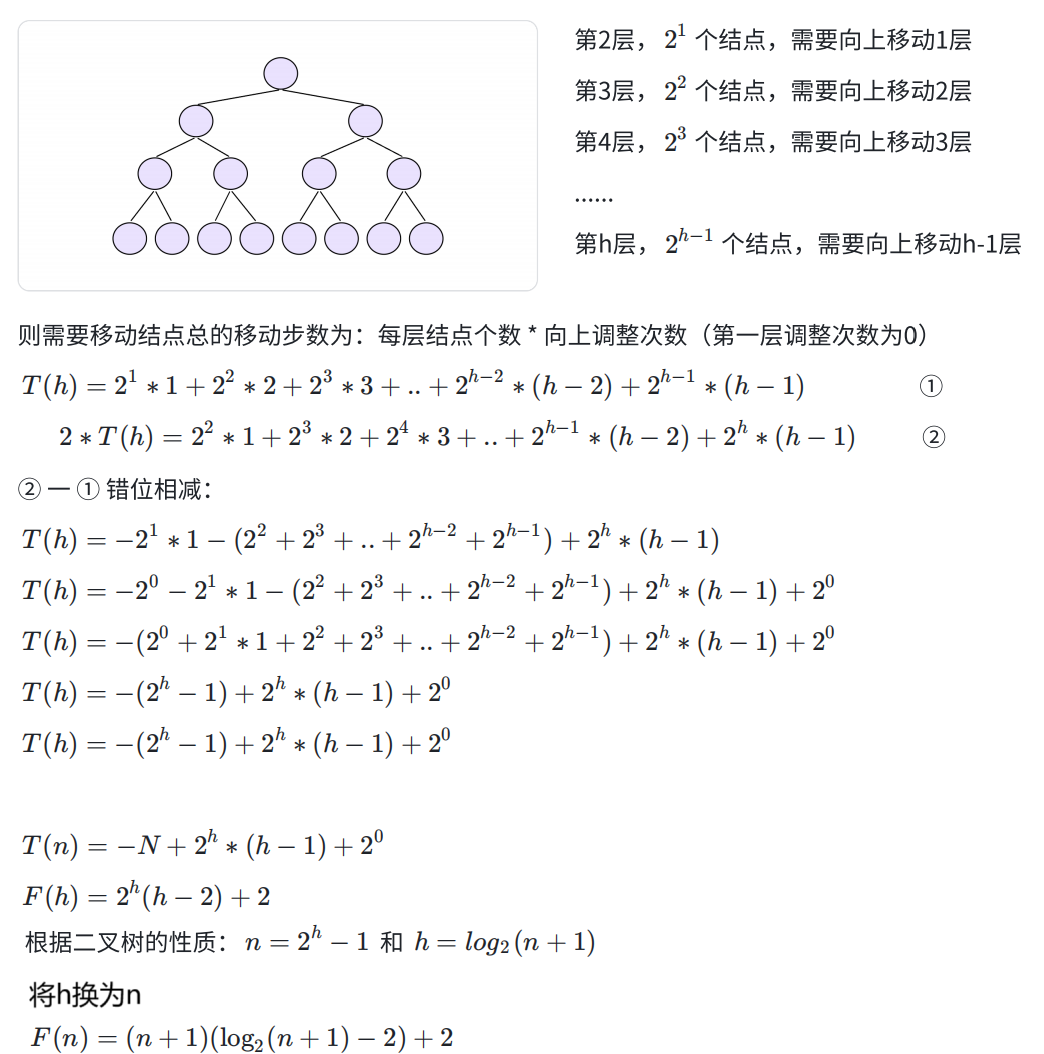
向上调整算法建堆：O(n*logn)--证明过程如下图：

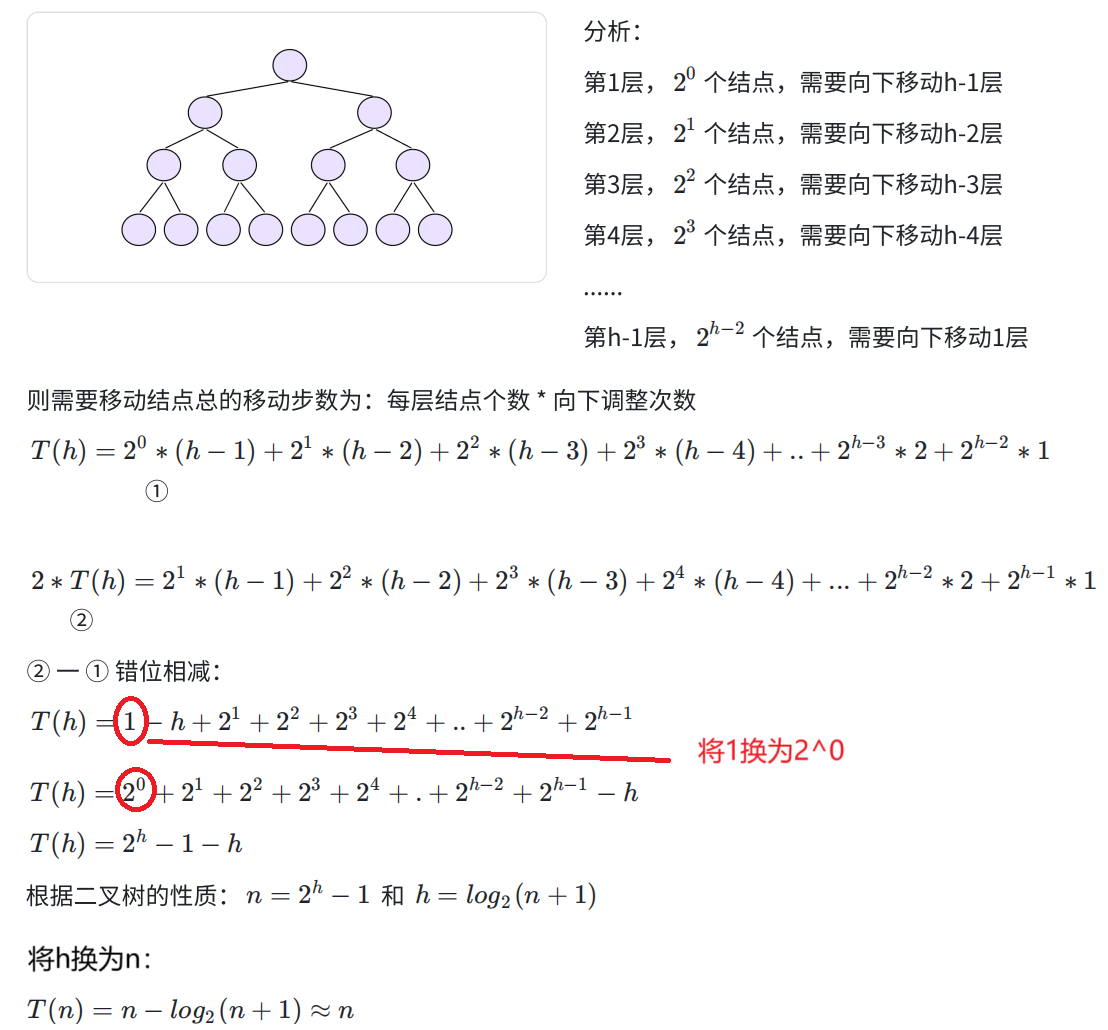
向下调整算法建堆：O(n)--证明过程如下图：

二.向上调整算法建堆和向下调整算法建堆的时间复杂度对比以及堆排序的时间复杂度

为什么向上调整算法和向下调整算法时间复杂度一样，但是他们建堆的时间复杂度会有区别呢？

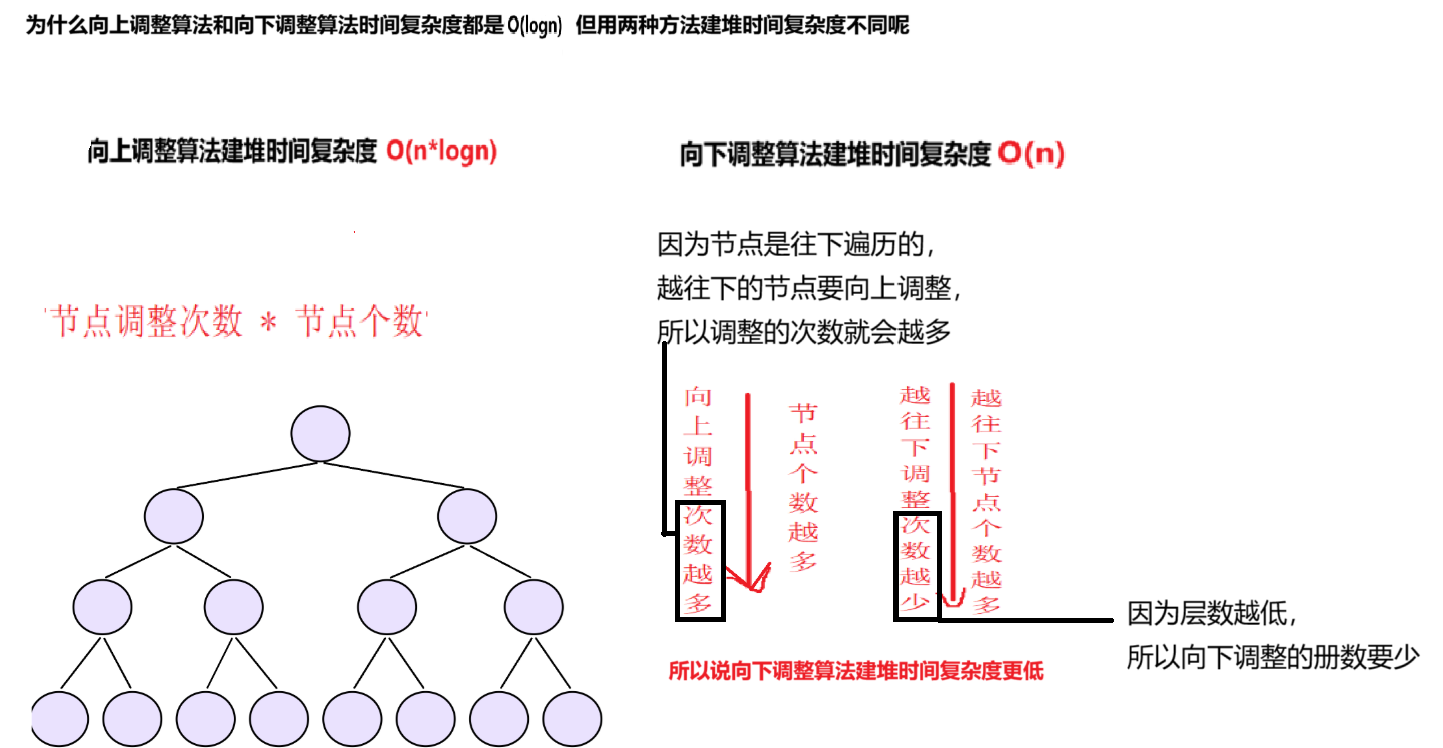
我们从图中可以看出,建堆的复杂度由节点调整次数和节点个数决定，向上调整算法建堆越往下节点个数越多，调整次数也越多，自然时间复杂度是没有向下调整算法低的。

堆排序的时间复杂度： O(n*logn)

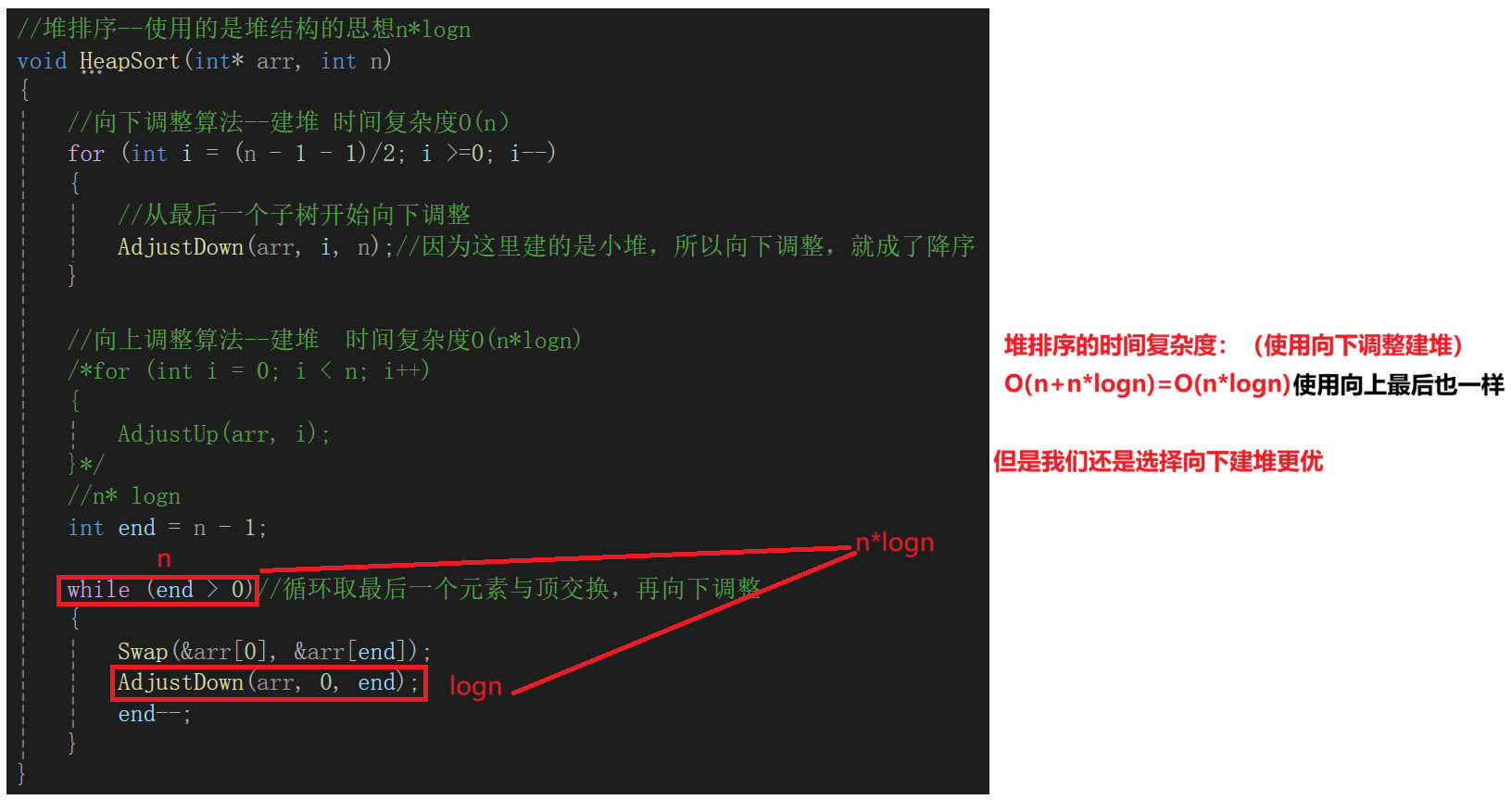
堆排序的时间复杂度为n*logn，这个时间复杂度算是比较优秀的一种排序算法

三、Top-K问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了 (可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决

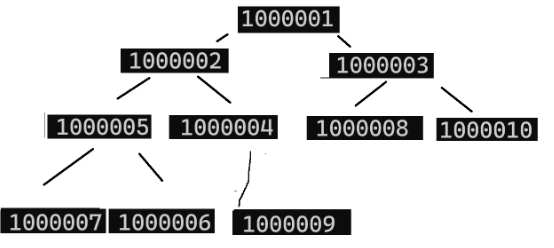
图解：

思路：

1.用数据前k个数据建堆

前k个最大的元素，则建小堆
前k个最小的元素，则建大堆

2.用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素：

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素

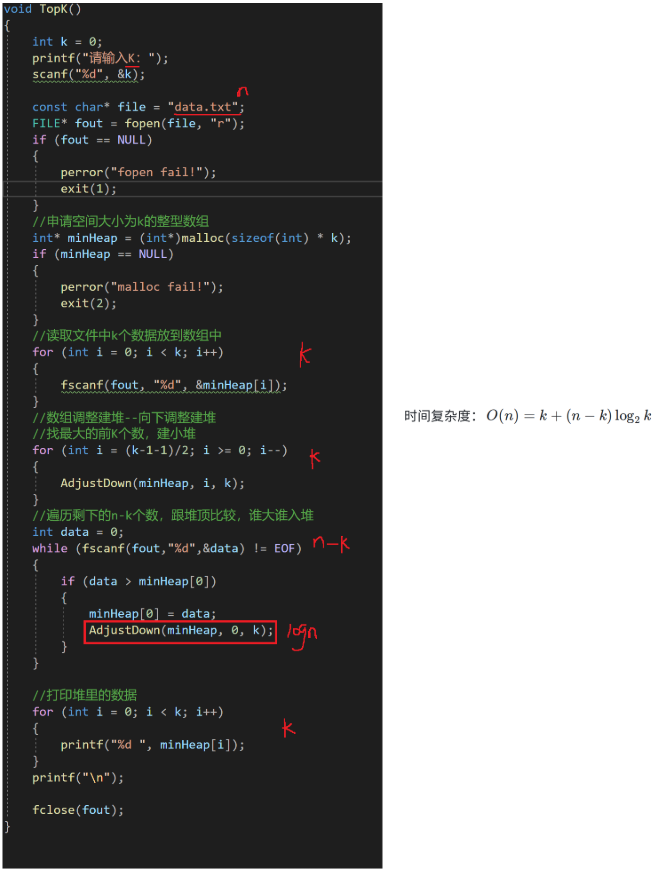
代码展示：

先给大家回顾一下向上调整算法和向下调整算法处理小堆的实现代码

//交换
void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//向上调整
void AdjustUp(HPDataType* arr, int child)
{
	int parent = (child - 1) / 2; 
	while (child > 0)
	{
		//建大堆 >
		//建小堆 <
		if (arr[child] < arr[parent])//小堆
		{
			Swap(&arr[child],&arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}


//向下调整
void AdjustDown(HPDataType* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//找大的孩子
		//建大堆 <
		//建小堆 >
		if (child + 1 < n && arr[child] > arr[child + 1])//xiao堆
		{
			child++;
		}
		//孩子和父亲比较
		//建大堆 <
		//建小堆 >
		if (arr[parent]> arr[child])//xiao堆
		{
			Swap(&arr[parent], &arr[child]);
			parent = child;
			child= parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

主代码:

void CreateNDate()
{
	// 造数据
	int n = 100000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}
	for (int i = 0; i < n; ++i)
	{
		int x = (rand() + i) % 1000000;
		fprintf(fin, "%d\n", x);
	}
	fclose(fin);
}

void TopK()
{
	int k = 0;
	printf("请输入k:\n");
	scanf("%d", &k);

	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen file!");
		exit(1);
	}
	//申请空间大小为k的整型数组
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail!");
		exit(2);
	}
	//读取文件中k个数据放到数组中
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	//数组调整建堆--向下调整建堆
	//找最大的k个数据--建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(minHeap, i, k);
	}
	//遍历剩下n-k个数据，大于堆顶的入堆
	int data = 0;
	while (fscanf(fout, "%d", &data) != EOF)
	{
		if (data > minHeap[0])
		{
			minHeap[0] = data;
			AdjustDown(minHeap, 0, k);
		}
	}
	//打印堆里的数据
	for (int i = 0; i < k; i++)
	{
		printf("%d ", minHeap[i]);
	}
	printf("\n");

	fclose(fout);
	fout = NULL;
}
int main()
{
	CreateNDate();
	TopK();
	return 0;
}