《动手学深度学习》读书笔记—10.5多头注意力

本文记录了自己在阅读《动手学深度学习》时的一些思考，仅用来作为作者本人的学习笔记，不存在商业用途。

注意力机制通过计算查询$\mathbf{q}$和每个键${\mathbf{k}}_{\mathbf{i}}$的注意力评分函数$a$，再将评分函数的计算结果经过$softmax$操作后产生注意力权重矩阵，最后通过矩阵乘法实现注意力权重矩阵引导值${\mathbf{v}}_i$产生相应的输出，具体来说就是下面的公式。
$$\begin{array}{r}\begin{array}{rl}f(\mathbf{q},({\mathbf{k}}_1,{\mathbf{v}}_1),\dots ,({\mathbf{k}}_m,{\mathbf{v}}_m))& =\sum _{i=1}^n\alpha (\mathbf{q},{\mathbf{k}}_i){\mathbf{v}}_i\\ & =\sum _{i=1}^n\mathrm{softmax}(a(\mathbf{q},{\mathbf{k}}_i)){\mathbf{v}}_i\end{array}\end{array}$$

在前面几节中我们都是这样计算注意力机制的，现在思考一个问题，我们能不能基于给定的查询、键和值使用同样的注意力评分函数$a$但是得到不同的输出？即只要求原始输入中的查询、键和值都是一样的，计算注意力汇聚时使用的注意力评分函数都是$a$，得到的最终输出结果不一样。

一个可行的思路是将查询、键和值经过不同的线性层进行变换，将变换后的查询、键和值作为查询、键和值，这样只要线性层中的权重矩阵$\mathbf{W}$和偏置$\mathbf{b}$不同，就能产生不同的输出结果。但是这样产生了很多组尺寸相同的输出，我们还需要将所有输出拼起来再通过一个线性层变换得到最终输出。这种想法被称为多头注意力。

🏷多头注意力的思路
多头注意力（multihead attention）的具体过程：用独立学习得到的$h$组不同的 线性投影（linear projections）来变换查询、键和值。 然后，这$h$组变换后的查询、键和值将并行地送到注意力汇聚中。 最后，将这$h$个注意力汇聚的输出拼接在一起， 并且通过另一个可以学习的线性投影进行变换， 以产生最终输出。

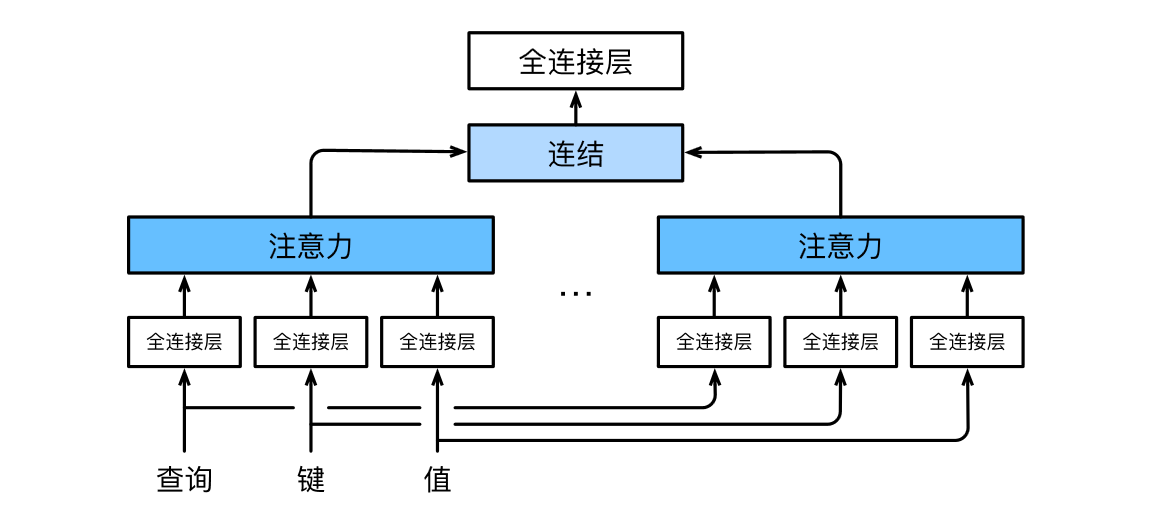
🏷多头注意力的具体过程

10.5.1 模型

给定查询$\mathbf{q}\in {\mathbb{R}}^{d_q}$、 键$\mathbf{k}\in {\mathbb{R}}^{d_k}$和 值$\mathbf{v}\in {\mathbb{R}}^{d_v}$， 每个注意力头${\mathbf{h}}_i（i=1,\dots ,h）$的计算方法为：
$${\mathbf{h}}_i=f({\mathbf{W}}_i^{(q)}\mathbf{q},{\mathbf{W}}_i^{(k)}\mathbf{k},{\mathbf{W}}_i^{(v)}\mathbf{v})\in {\mathbb{R}}^{p_v}$$
其中，可学习的参数包括${\mathbf{W}}_i^{(q)}\in {\mathbb{R}}^{p_q\times d_q}$、${\mathbf{W}}_i^{(k)}\in {\mathbb{R}}^{p_k\times d_k}$和${\mathbf{W}}_i^{(v)}\in {\mathbb{R}}^{p_v\times d_v}$，以及代表注意力汇聚的函数$f$。$f$可以是10.3 注意力评分函数中的加性注意力和缩放点积注意力。多头注意力的输出需要经过另一个线性转换，它对应着$h$个头连结后的结果，因此其可学习参数是${\mathbf{W}}_o\in {\mathbb{R}}^{p_o\times h{p}_v}$:
$$\begin{array}{r}{\mathbf{W}}_o\left[\begin{array}{c}{\mathbf{h}}_1\\ ⋮\\ {\mathbf{h}}_h\end{array}\right]\in {\mathbb{R}}^{p_o}.\end{array}$$
每个头都可能会关注输入的不同部分， 可以表示比简单加权平均值更复杂的函数。

10.5.2 实现

在实现过程中通常选择缩放点积注意力作为每一个注意力头。 为了避免计算代价和参数代价的大幅增长， 我们设定$p_q=p_k=p_v=p_o/h$。 值得注意的是，如果将查询、键和值的线性变换的输出数量设置为$p_{q}h=p_{k}h=p_{v}h=p_o$ ， 则可以并行计算$h$个头。 在下面的实现中，$p_o$是通过参数num_hiddens指定的。

🏷并行的意思

import math
import torch
from torch import nn
from d2l import torch as d2l

#@save
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        # 头的数量
        self.num_heads = num_heads
        # 缩放点击注意力, 输出是(批量大小，查询的步数，值的维度)
        self.attention = d2l.DotProductAttention(dropout)
        # 查询、键和值经过线性层变换(这里已经是复制了num_heads次拼接后的查询、键和值了)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        # 最终线性层, 将不同head拼接后的输出再次映射
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        # 输入的查询、键和值的形状(批量大小，查询或者“键－值”对的个数，隐藏层维数)
        # 注意,这里是将原始的查询、键和值复制了num_heads次后拼起来的查询、键和值
        # valid_lens　的形状:(批量大小，)或(批量大小，查询的个数)
        # 经过变换后，输出的查询、键和值的形状:
        # (批量大小*num_heads，查询或者“键－值”对的个数，隐藏层维数/num_heads)
        # 这里的变换实际上将不同head的查询、键和值进行了分别映射, 只不过使用了矩阵乘法后看不出来
        # transpose_qkv把不同head的映射分开
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # 得到不同head的output
        # output的形状:(批量大小*num_heads，查询的个数，隐藏层维数/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # transpose_output将不同head的output拼接起来得到output_concat
        # output_concat的形状:(批量大小，查询的个数，隐藏层维数)
        output_concat = transpose_output(output, self.num_heads)
        # 将拼接后的输出送入线性层得到最终输出
        return self.W_o(output_concat)

为了能够使多个头并行计算， 上面的MultiHeadAttention类将使用下面定义的两个转置函数。 具体来说，transpose_output函数反转了transpose_qkv函数的操作。

#@save
def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    # 输入X的形状:(批量大小，查询或者“键－值”对的个数，隐藏层维数)
    # 输出X的形状:(批量大小，查询或者“键－值”对的个数，num_heads，隐藏层维数/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # 输出X的形状:(批量大小，num_heads，查询或者“键－值”对的个数,隐藏层维数/num_heads)
    X = X.permute(0, 2, 1, 3)

    # 最终输出的形状:(批量大小*num_heads,查询或者“键－值”对的个数, 隐藏层维数/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])


#@save
def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    # 输入X的形状:(批量大小*num_heads,查询或者“键－值”对的个数, 隐藏层维数/num_heads)
    # reshape后:(批量大小, num_heads, 查询或者“键－值”对的个数, 隐藏层维数/num_heads)
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    # permute(0, 2, 1, 3):(批量大小, 查询或者“键－值”对的个数, num_heads, 隐藏层维数/num_heads)
    X = X.permute(0, 2, 1, 3)
    # reshape后:(批量大小，查询或者“键－值”对的个数，隐藏层维数)
    return X.reshape(X.shape[0], X.shape[1], -1)

下面使用键和值相同的小例子来测试MultiHeadAttention类。 多头注意力输出的形状是（batch_size，num_queries，num_hiddens）。

# 隐藏层维数:100, 头的数量:5
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                               num_hiddens, num_heads, 0.5)
attention.eval()

运行结果

MultiHeadAttention(
  (attention): DotProductAttention(
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (W_q): Linear(in_features=100, out_features=100, bias=False)
  (W_k): Linear(in_features=100, out_features=100, bias=False)
  (W_v): Linear(in_features=100, out_features=100, bias=False)
  (W_o): Linear(in_features=100, out_features=100, bias=False)
)

# 批量大小:2, 查询的数量: 4
batch_size, num_queries = 2, 4
# 键值对数量:6, 第一个序列的有效长度是3, 第二个序列的有效长度是2
num_kvpairs, valid_lens =  6, torch.tensor([3, 2])
# 创建查询X
X = torch.ones((batch_size, num_queries, num_hiddens))
# 创建键和值Y
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
attention(X, Y, Y, valid_lens).shape

运行结果

torch.Size([2, 4, 100])

10.5.3 小结

• 多头注意力融合了来自于多个注意力汇聚的不同知识，这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
• 基于适当的张量操作，可以实现多头注意力的并行计算。