53. 最大子数组和
力扣题目链接
给你一个整数数组nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组(数组中连续的非空元素序列)是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
一、暴力解法【都会超时】
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
"""
最暴力解法
时间复杂度 O(n^3):遍历i、遍历j、sum(nums[i:j+1])都是O(n)。
空间复杂度 O(1)
"""
max_sum = float('-inf')
for i in range(len(nums)):
for j in range(i, len(nums)): # j=i的情况也要
sum_ = sum(nums[i:j+1])
max_sum = max(max_sum, sum_)
return max_sum
###### 第二暴力(但其实差不多) ######
def maxSubArray(self, nums: List[int]) -> int:
"""
时间复杂度 O(n^2):遍历i、遍历j
空间复杂度 O(1)
"""
max_sum = float('-inf')
for i in range(len(nums)):
cur_sum = 0
for j in range(i, len(nums)):
cur_sum += nums[j] # 累加,避免重复计算
max_sum = max(max_sum, cur_sum)
return max_sum
二、Kadane’s 算法
- 【思路】Kadane’s 算法是解决最大子数组和问题的经典动态规划算法,其核心思想是:
对于数组中的每个位置,我们只需要决定:是重新开始一个新的子数组,还是将当前元素加入到之前的子数组中:
- 如果之前子数组的和为负数(
num > cur_sum + num),那么不如直接从当前元素重新开始;- 如果之前子数组的和为正数(
num < cur_sum + num),那么加上当前元素会让总和更大,所以继续延长。
这样我们就将问题转化为:在每个位置,选择局部最优解,最终得到全局最优解。
【步骤】
1. 初始化:
cur_sum:记录以当前位置结尾的最大子数组和
max_sum:记录全局最大子数组和2. 遍历数组:
对于每个元素num,计算以它结尾的最大子数组和
状态转移方程:cur_sum = max(num, cur_sum + num)
更新全局最大值:max_sum = max(max_sum, cur_sum)3. 返回结果: 遍历完返回
max_sum.
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
# 初始化:第一个元素既是当前最大和,也是全局最大和
cur_sum = max_sum = nums[0]
# 从第二个元素开始遍历
for num in nums[1:]:
cur_sum = max(num, cur_sum + num) # 要么重新开始(num大),要么继续累加(num小)
max_sum = max(max_sum, cur_sum) # 更新全局最大值
return max_sum
- 时间复杂度 O(n)
- 空间复杂度 O(1)
56. 合并区间
力扣题目链接
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
(若没有1 <= intervals.length 条件的话别忘记加 if not intervals: return [])
【思路】排序 + 贪心合并
【步骤】
1. 排序: 按每个区间的起始位置进行排序,让可能重叠的区间相邻2. 初始化: 将第一个区间加入结果数组
3. 遍历合并:
- 对于每个后续区间,检查是否与**结果数组最后一个区间(上一个区间)**重叠
- 若重叠:更新最后一个区间的结束位置
- 如若不重叠:直接将当前区间加入结果数组
重叠条件:
cur_start ≤ last_end(注意等号)
对于排序后的两个相邻区间[a, b]和[c, d](其中a ≤ c):
如果b >= c,则两个区间重叠,合并后的区间为[a, max(b, d)]4. 返回结果
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
intervals.sort() # 默认按第一个元素排序,或者显式指定intervals.sort(key=lambda x: x[0])
res = [intervals[0]]
for start, end in intervals[1:]:
if start <= res[-1][1]: # 与 上一个区间的end 比较
res[-1][1] = max(res[-1][1], end) # 若能合并,则合并进去(只用改end就好)
else:
res.append([start, end]) # 若不能合并,则直接添加新区间
return res
- 时间复杂度 O(n log n)
- 空间复杂度 O(n)
189. 轮转数组
力扣题目链接
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105进阶:
尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗?
以下五种方法,除暴力解法外都不会超时,但若要求空间复杂度为 O(1) ,则直接看法四五。(法四最推荐)
一、暴力解法(会超时)
- 【思路】每次向右移动1,逐个移动(k次)
def rotate(nums, k):
n = len(nums)
k = k % n
for _ in range(k):
# 保存最后一个元素
temp = nums[-1]
# 每个元素向右移动一位
for i in range(n - 1, 0, -1):
nums[i] = nums[i - 1]
# 将最后一个元素放到开头
nums[0] = temp
- 时间复杂度 O(n×k)
- 空间复杂度 O(1)
二、使用额外数组(用了额外空间)
- 【思路】
- 创建一个新数组,将每个元素放到轮转后的正确位置
- 元素
nums[i]轮转后的新位置是(i + k) % n
def rotate(nums, k):
n = len(nums)
k = k % n # 取余数,k>n时也涵盖,k<n时余数就为k
# 创建新数组存储结果
rotated = [0] * n
# 将每个元素放到轮转后的位置
for i in range(n):
rotated[(i + k) % n] = nums[i] # (i + k) % n = | (i + k), if (i+k) < n
# | (i + k) - m n, if (i+k) > n
# 将结果复制回原数组
nums[:] = rotated # 这算不算是“拆包”?(类似于a,b,c = [1,2,3])
- 时间复杂度 O(n)
- 空间复杂度 O(n)
三、双端队列(用了额外空间)
- 【思路】从队尾取出k个元素,放到队头。(非常直观!)
from collections import deque
def rotate(nums, k):
n = len(nums)
k = k % n
dq = deque(nums) # 转换为双端队列
for _ in range(k):
dq.appendleft(dq.pop()) # 从右端弹出,插入到左端
nums[:] = list(dq) # 将结果复制回原数组
- 时间复杂度 O(n + k) :转换为队列&转换回数组 操作都是O(n),加上k次O(1)的队列操作。
- 空间复杂度 O(n)
四、三次反转【最优】
- 【例子】把 [1,2,3,4,5,6,7] 变成 [5,6,7,1,2,3,4]
- 首先要 5,6,7 在 1,2,3,4 前面,这可以通过反转整个数组做到。
- 反转后变成 [7,6,5,4,3,2,1],发现前三个数需要反转,后四个数需要反转,就得到了最终结果。
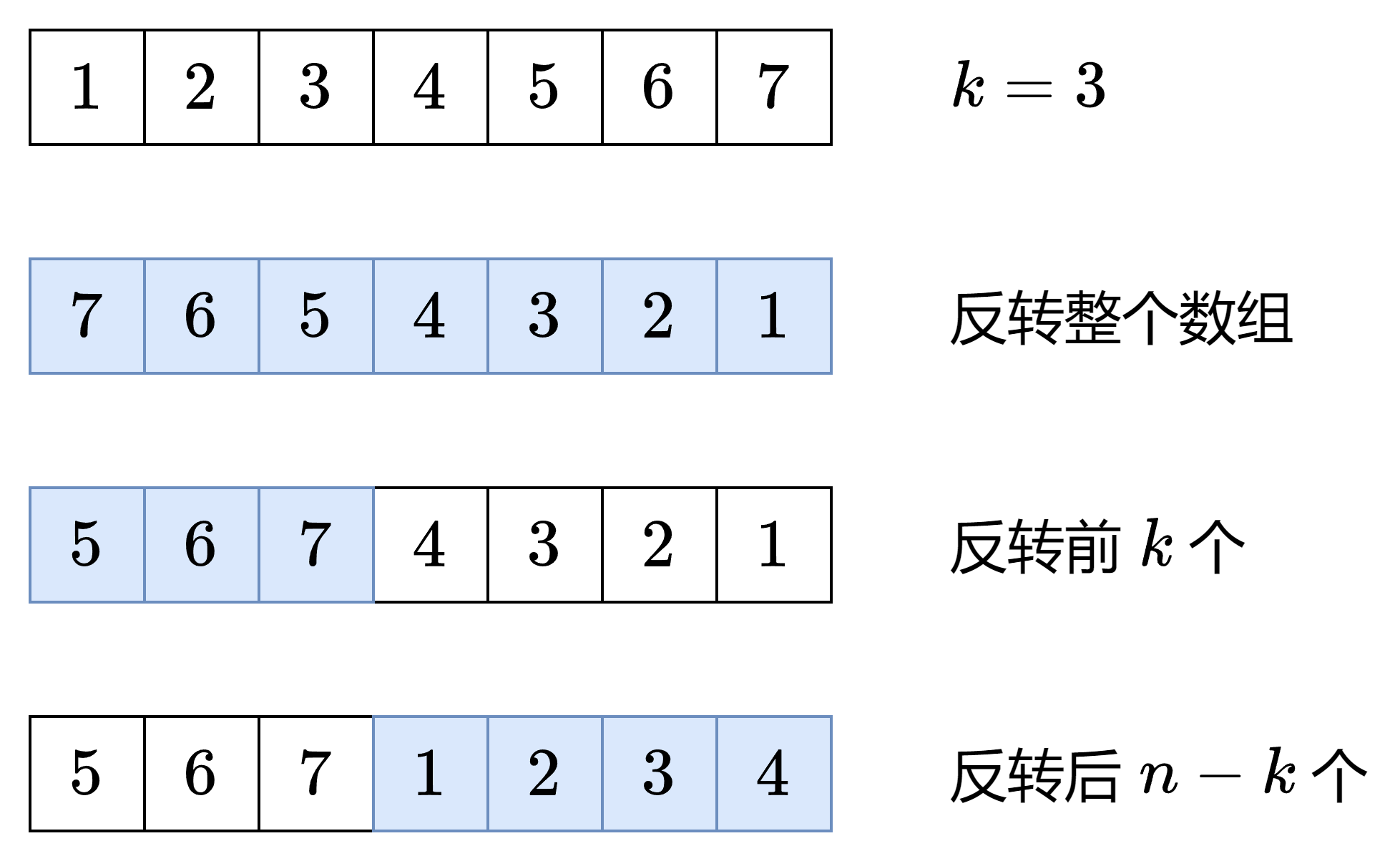
- 数学证明见原帖:灵茶山艾府
# 注:请勿使用切片,会产生额外空间
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
def reverse(start: int, end: int) -> None:
while start < end:
nums[start], nums[end] = nums[end], nums[start]
start += 1
end -= 1
n = len(nums)
k %= n # 轮转 k 次等于轮转 k % n 次
reverse(0, n - 1) # 反转整个数组
reverse(0, k - 1) # 反转前k个
reverse(k, n - 1) # 反转后n-k个
- 时间复杂度 O(n)
- 空间复杂度 O(1)
- 【但其实】我试了直接用切片或reverse()也是O(1),可能是“有一定风险创建临时列表”?但代码更简洁:
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
k %= len(nums) # 两行并一行了k = k % n
nums.reverse()
nums[:k] = reversed(nums[:k]) # 或 nums[:k] = nums[:k][::-1]
nums[k:] = reversed(nums[k:]) # 或 nums[k:] = nums[k:][::-1]
五、环状替换【最优但逻辑复杂】
【思路】
将每个元素直接放到其最终位置
如果遇到环,则从下一个未访问的位置开始新的环【步骤】
- 从位置0开始,将元素放到其目标位置
- 继续处理被替换位置的元素,直到回到起点(形成环)
- 如果还有未处理的元素,从下一个位置开始新的环
def rotate(nums, k):
n = len(nums)
k = k % n
count = 0 # 已处理的元素数量
start = 0 # 当前环的起始位置
while count < n:
current = start
prev = nums[start]
# 处理当前环
while True:
next_idx = (current + k) % n # 计算目标位置
nums[next_idx], prev = prev, nums[next_idx] # 交换元素
current = next_idx
count += 1
# 如果回到起点,环结束
if start == current:
break
start += 1 # 开始下一个环
- 时间复杂度 O(n)
- 空间复杂度 O(1)
238. 除自身以外数组的乘积
力扣题目链接
给你一个整数数组nums,返回数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在O(n)时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
【进阶】:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
一、暴力解法
【思路】对于每个位置i,计算除nums[i]外所有元素的乘积。
def productExceptSelf(nums):
n = len(nums)
res = [1] * n
for i in range(n):
product = 1
for j in range(n):
if i != j: # 跳过自己
product *= nums[j]
res[i] = product
return res
- 时间复杂度 O(n^2):双层循环嵌套
- 空间复杂度 O(1):不算输出数组的话
二、前后缀数组
- 【思路】用两个数组
pre和suf分别表示i左右边所有数的乘积,则answer[i]=pre[i]⋅suf[i]。- 定义
pre[i]表示从nums[0]到nums[i−1]的乘积 (i>0——从第二个开始)。 - 定义
suf[i]表示从nums[i+1]到nums[n−1]的乘积 (i<n-1——从第二个开始)。
- 定义
- 【步骤】
- 初始化并创建
pre;(注意pre[0]初始化为1而不是nums[0]!) - 初始化并创建
suf;(注意suf[n-1]初始化为1而不是nums[n-1]!) - 返回它们的乘积数组(结果数组)
- 初始化并创建
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
pre = [1] * n
for i in range(1, n): # 注意要从第二个元素开始!!
pre[i] = pre[i - 1] * nums[i - 1]
suf = [1] * n
for i in range(n-2, -1, -1): # 注意要从第二个元素开始!!
suf[i] = suf[i + 1] * nums[i + 1]
return [p * s for p, s in zip(pre, suf)]
- 时间复杂度 O(n)
- 空间复杂度 O(n):2n ~ O(n),题目说「输出数组不被视为额外空间」所以不是3n。
三、前后缀数组【优化版】——不使用额外空间
- 【思路】先计算
suf,然后一边计算pre,一边把pre直接乘到suf[i]中。最后返回suf。
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
n = len(nums)
suf = [1] * n
for i in range(n - 2, -1, -1):
suf[i] = suf[i + 1] * nums[i + 1]
pre = 1
for i, num in enumerate(nums):
# 此时 pre 为 nums[0] 到 nums[i-1] 的乘积,直接乘到 suf[i] 中
suf[i] *= pre
pre *= num
return suf
- 时间复杂度 O(n)
- 空间复杂度 O(1):这种做法比上面少遍历了一次,且题目说「输出数组不被视为额外空间」。
41. 缺失的第一个正数
力扣题目链接
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
解释:最小的正数 1 没有出现。
零、关键点【以下所有算法都基于此】
对于长度为
n的数组,缺失的第一个正数一定在[1, n+1]范围内。
【为什么?】
- 如果数组包含 1, 2, 3, …, n,那么缺失的第一个正数是 n+1
- 如果数组缺少 [1, n] 中的任何一个数,那么答案就是这个缺失的数
- 所以答案的范围被限制在 [1, n+1]
一、原地哈希
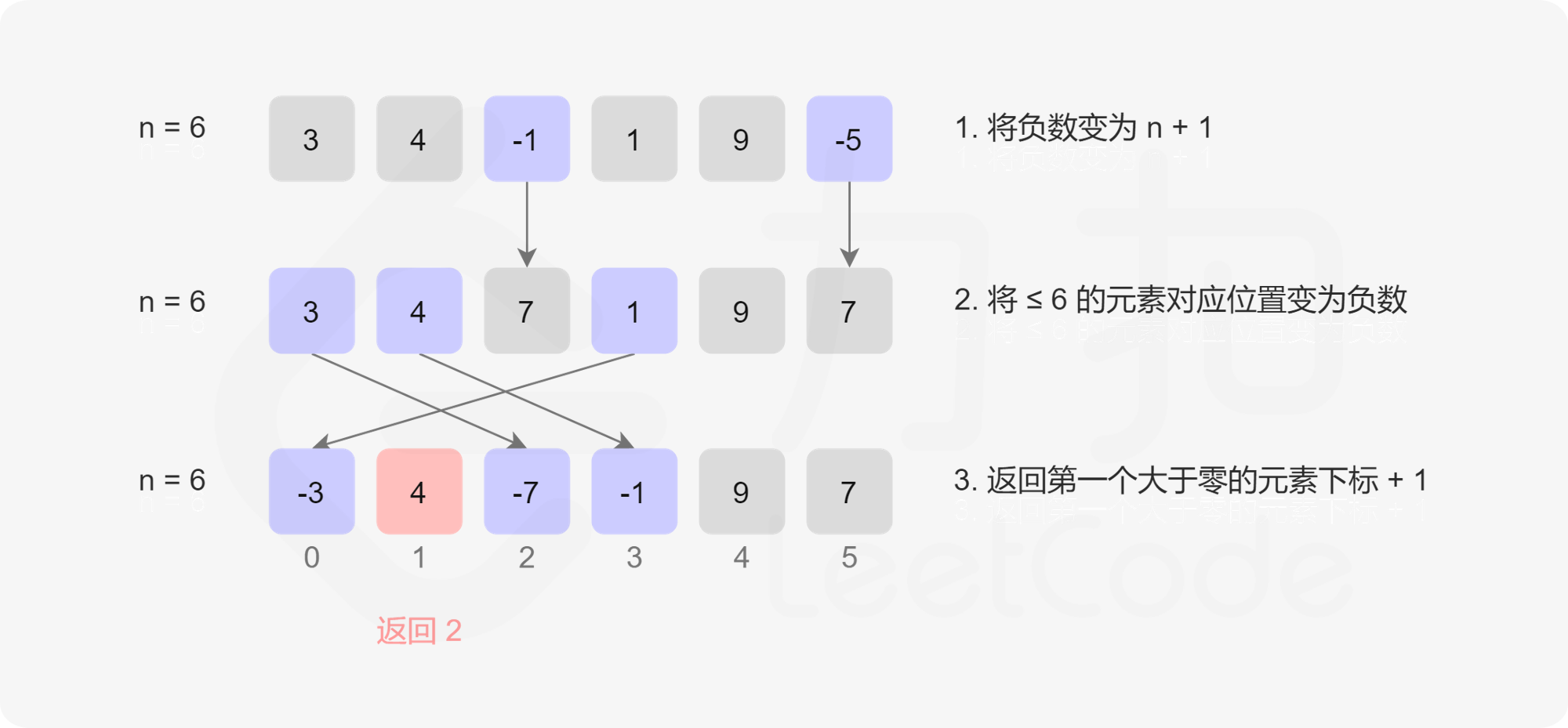
- 【思路】既然答案在 [1, n+1] 范围内,我们可以将数组本身作为哈希表,让 nums[i] 存储数字 i+1 是否存在的信息,通过负号标记存在性。
- 【步骤】
步骤1:预处理 - 处理非正数和超范围数
将≤ 0的数和> n的数都替换为n+1(一个不影响结果的数)步骤2:标记存在性
遍历数组,对于每个数字 x(取绝对值)
如果1 ≤ |x| ≤ n,将nums[|x|-1]标记为负数
负号表示数字x存在于原数组中步骤3:查找答案
遍历数组,找到第一个正数的位置i
答案就是i+1
如果所有数都是负数,答案是n+1
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
# 第一遍:预处理,将无效数字替换
for i in range(n):
if nums[i] <= 0 or nums[i] > n:
nums[i] = n + 1 # 替换为一个不会影响结果的数
# 第二遍:标记存在的数字
for i in range(n):
num = abs(nums[i]) # 取绝对值,可能已被标记为负
if 1 <= num <= n:
index = num - 1 # 数字num对应的索引
if nums[index] > 0: # 避免重复标记
nums[index] = -nums[index] # 用负号标记
# 第三遍:找答案
for i in range(n):
if nums[i] > 0: # 第一个未被标记的位置
return i + 1
return n + 1 # 1~n都存在,答案是n+1
- 时间复杂度 O(n)
- 空间复杂度 O(1)
二、置换排序
- 【思路】待补充
n = len(nums)
# 将每个数字放到正确位置:nums[i] = i+1
for i in range(n):
while 1 <= nums[i] <= n and nums[nums[i] - 1] != nums[i]:
# 交换 nums[i] 和 nums[nums[i] - 1]
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
# 找到第一个不在正确位置的数
for i in range(n):
if nums[i] != i + 1:
return i + 1
return n + 1
- 时间复杂度 O(n)
- 空间复杂度 O(1)
三、哈希集合
【思路】从小到大遍历 [1, 2,…, n+1] ,直到第一个不在set(nums)中的就是答案。——既然缺失的第一个正数一定在 [1, n+1] 范围内,就一定能找到,不会无穷循环。
def firstMissingPositive(nums):
num_set = set(nums)
i = 1
while i in num_set: #
i += 1
return i
- 时间复杂度 O(n)
- 空间复杂度 O(n):要新建set所以不满足题目要求
四、排序遍历
【思路】先排序,再设一个target变量,遍历时逐次加1,首次没“跟上”该元素时就是答案。
def firstMissingPositive(nums):
nums.sort()
target = 1
for num in nums:
if num == target:
target += 1
elif num > target:
break
return target
- 时间复杂度 O(n logn) :不满足题目要求
- 空间复杂度 O(1)
各解法对比
| 解法 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|
| 原地哈希 | O(n) | O(1) | 最优解,巧妙利用负号标记 |
| 置换排序 | O(n) | O(1) | 直观,将数字放到正确位置 |
| 哈希集合 | O(n) | O(n) | 简单直接,但空间不符合要求 |
| 排序遍历 | O(n logn) | O(1) | 思路简单,但时间复杂度不optimal |