梯度下降法
1、基本思想:先设定一个学习率η\etaη,参数沿梯度的反方向移动。假设需要更新的参数为w,梯度为g,更新策略可以表示为
w←w−η∗g w \leftarrow w - \eta*g w←w−η∗g
2、梯度下降算法有三种不同的形式:
- BGD(Batch Gradient Descent):批量梯度下降,每次参数更新使用
所有样本 - SGD(Stochastic Gradient Descent):随机梯度下降,每次参数更新只使用
一个样本 - MBGD(Mini-Batch Gradient Descent):小批量梯度下降,每次参数更新使用
小部分数据样本
三个优化算法虽然采用的数据量不同,但是步骤相同
step1g=∂loss∂wstep2求梯度的平均值step3更新权重w←w−η∗g \text{step1} \qquad g = \frac{\partial loss}{\partial w} \\ step2 \qquad 求梯度的平均值 \\ step3 \qquad 更新权重 w \leftarrow w - \eta * g step1g=∂w∂lossstep2求梯度的平均值step3更新权重w←w−η∗g
缺点
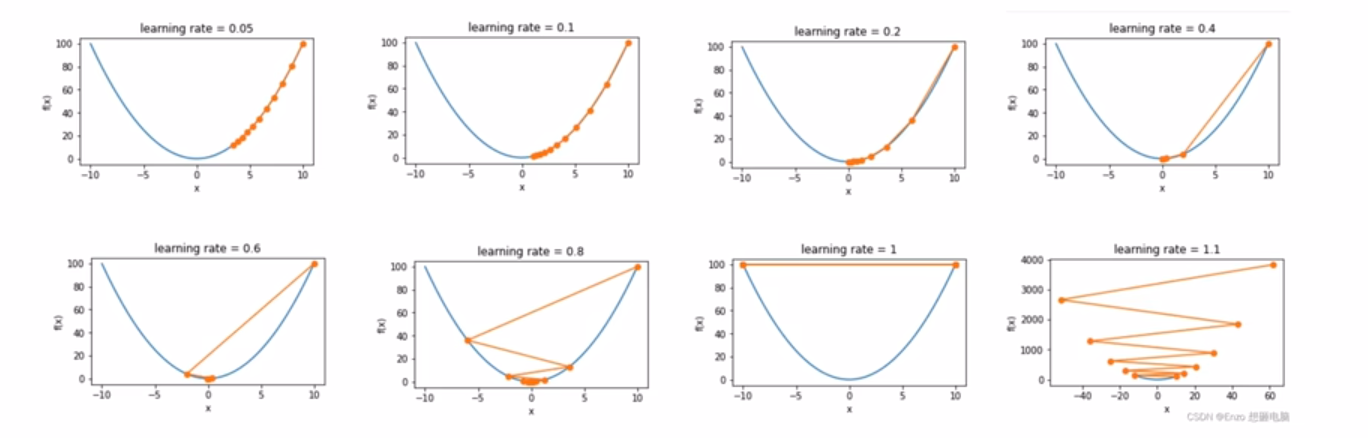
- 对超参数学习率敏感:过小导致收敛速度过慢,过大又越过极值点
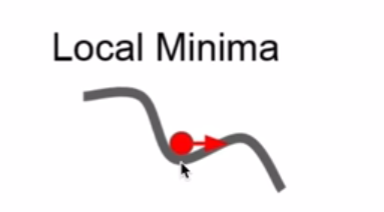
- 容易卡在鞍点位置,即梯度为0的地方
- 在比较平坦的区域,由于梯度接近于0,优化算法会因误判,还未到达极值点,就提前结束迭代,陷入局部最小值
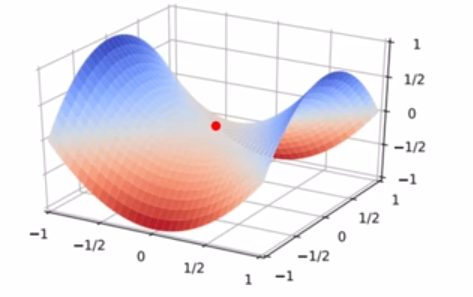
多维梯度下降法
即有多个参数需要优化X=[x1,x2....,xd]TX = [x_1,x_2....,x_d]^TX=[x1,x2....,xd]T
多元损失函数,梯度也是多元的,由d个偏导数组成
∇f(X)=∇fx∇x1,∇fx∇x2..,∇fx∇xdT \nabla f(X) = {\frac{\nabla f_x}{\nabla x_1},\frac{\nabla f_x}{\nabla x_2}..,\frac{\nabla f_x}{\nabla x_d}}^T ∇f(X)=∇x1∇fx,∇x2∇fx..,∇xd∇fxT
xi←xi−η∗∇f(X) x_i \leftarrow x_i - \eta * \nabla f(X) xi←xi−η∗∇f(X)
构造一个目标函数f(x)=x12+2x22f(x) = x_1^2 + 2x_2^2f(x)=x12+2x22,损失函数的梯度为∇f(x)=[2x1,,4x2]T\nabla f(x) = [2x_1,,4x_2]^T∇f(x)=[2x1,,4x2]T
动量
思想:让参数的更新具有惯性,每一步更新都是由前面梯度的累积v和当前点梯度g组合而成
公式:
累计梯度更新:v←αv+(1−α)gv \leftarrow \alpha v+(1-\alpha)gv←αv+(1−α)g,其中α\alphaα为动量参数,v为累计梯度,η\etaη为学习率。
梯度更新:x←x−η∗vx \leftarrow x- \eta*vx←x−η∗v
优点:
- 加快收敛帮助参数在正确的方向上加速前进
- 跳出局部最小值
Adagrad
自适应学习率优化算法
之前的随机梯度下降法,对所有的参数,都是使用相同的、固定的学习率进行优化,但是不同的参数的梯度差异可能很大,使用相同的学习率,效果不会很好。

Adagrad思想:对于不同参数,设置不同的学习率,如果一个参数的梯度一直很大,那么其对应的学习率就变小一点,防止振荡,如果梯度小,就学习率大一点。
方法:对于每个参数,初始化一个累计平方梯度 r=0,然后每次将该参数的梯度平方求和累加到这个变量r上:
r←r+g2 r \leftarrow r +g^2 r←r+g2
更新参数时,学习率为:
ηr+σ,σ为极小值,防止分母为0 \frac{\eta}{\sqrt{r+\sigma}},\sigma为极小值,防止分母为0 r+ση,σ为极小值,防止分母为0
权重更新:
w←w−ηr+σ∗g w \leftarrow w - \frac{\eta}{\sqrt{r+ \sigma}}*g w←w−r+ση∗g
RMSProp
RMSProp:Root Mean Square Propagation 均方根传播
RMSProp在Adagrad的基础上,进一步在学习率的方向上优化
累计平方梯度:r←λr+(1−λ)g2r \leftarrow \lambda r +(1-\lambda)g^2 r←λr+(1−λ)g2
权重更新:
w←w−ηr+σ∗g w \leftarrow w - \frac{\eta}{\sqrt{r+ \sigma}}*g w←w−r+ση∗g
就是多了一个λ\lambdaλ衰减系数
Adam
缝合怪,缝合了上述所有优化器
1、梯度方面增加momentum, 使用累计梯度:v←αv+(1−α)gv \leftarrow \alpha v+(1-\alpha)gv←αv+(1−α)g
2、同RMSProp优化算法一样,对学习率进行优化,使用累计平方梯度:
r←λr+(1−λ)g2r \leftarrow \lambda r +(1-\lambda)g^2 r←λr+(1−λ)g2
3、偏差纠正
v^=v1−αt,r=r1−λt \hat{v} = \frac{v}{1-\alpha^t},r=\frac{r}{1-\lambda^t} v^=1−αtv,r=1−λtr
Adam 的偏差纠正就是通过 m^,t^\hat{m},\hat{t}m^,t^ 把指数加权平均在初期“偏小”的问题修正掉,从而保证优化器在早期能稳定、合理地更新参数。
初始v=0,r=0
