3.5 Margin and Regularization
3.5 边界和正则化
边界和正则化
求一个点距离线性分类器的距离
考虑一个线性分类器,其分界面为:
f ( x ) = w T x + b = 0 对于所有在边界上的 x f(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + b = 0 \quad \text{对于所有在边界上的} \ \mathbf{x} f(x)=wTx+b=0对于所有在边界上的 x
向量 w \mathbf{w} w 垂直于线性判别式

证明过程
假设在边界上有两个点 x ( 1 ) \mathbf{x}^{(1)} x(1) 和 x ( 2 ) \mathbf{x}^{(2)} x(2):
f ( x ( 1 ) ) = w T x ( 1 ) + b = 0 (1) f(\mathbf{x}^{(1)}) = \mathbf{w}^T \mathbf{x}^{(1)} + b = 0 \tag{1} f(x(1))=wTx(1)+b=0(1)
f ( x ( 2 ) ) = w T x ( 2 ) + b = 0 (2) f(\mathbf{x}^{(2)}) = \mathbf{w}^T \mathbf{x}^{(2)} + b = 0 \tag{2} f(x(2))=wTx(2)+b=0(2)
用式 (2) 减去式 (1):
w T ( x ( 2 ) − x ( 1 ) ) = 0 \mathbf{w}^T \left( \mathbf{x}^{(2)} - \mathbf{x}^{(1)} \right) = 0 wT(x(2)−x(1))=0由此可得: w ⊥ ( x ( 2 ) − x ( 1 ) ) \mathbf{w} \perp \left( \mathbf{x}^{(2)} - \mathbf{x}^{(1)} \right) w⊥(x(2)−x(1))
即权重向量 W 与边界上的任意两个点的连线方向垂直。
求距离margin
设 x ( s ) \mathbf{x}^{(s)} x(s) 是特征空间中的一个点,它在边界上的投影为 x ( p ) \mathbf{x}^{(p)} x(p):
f ( x ( p ) ) = w T x ( p ) + b = 0 (3) f(\mathbf{x}^{(p)}) = \mathbf{w}^T \mathbf{x}^{(p)} + b = 0 \tag{3} f(x(p))=wTx(p)+b=0(3)

根据向量计算, x ( s ) = x ( p ) + r w ^ (4) \mathbf{x}^{(s)} = \mathbf{x}^{(p)} + r \hat{\mathbf{w}}\tag{4} x(s)=x(p)+rw^(4)
w ^ \hat{\mathbf{w}} w^是 w \mathbf{w} w的方向向量,长度为1,
w ^ = w ∥ w ∥ (5) \hat{\mathbf{w}}=\frac{\mathbf{w}}{\|\mathbf{w}\|}\tag{5} w^=∥w∥w(5)
求训练数据点 x ( s ) \mathbf{x}^{(s)} x(s)的标签值, f ( x ( s ) ) = w T x ( s ) + b f(\mathbf{x}^{(s)}) = \mathbf{w}^T \mathbf{x}^{(s)} + b f(x(s))=wTx(s)+b, 将(4)代入,
f ( x ( s ) ) = w T ( x ( p ) + r w ^ ) + b f ( x ( s ) ) = w T x ( p ) + r w T w ^ + b f(\mathbf{x}^{(s)})= \mathbf{w}^T \left( \mathbf{x}^{(p)} + r \hat{\mathbf{w}} \right) + b\\ \\ f(\mathbf{x}^{(s)})= \mathbf{w}^T \mathbf{x}^{(p)} + r \mathbf{w}^T \hat{\mathbf{w}} + b\\ f(x(s))=wT(x(p)+rw^)+bf(x(s))=wTx(p)+rwTw^+b将(5)代入,
f ( x ( s ) ) = w T x ( p ) + b + r w T w ∥ w ∥ f(\mathbf{x}^{(s)})= \mathbf{w}^T \mathbf{x}^{(p)} + b + r \, \mathbf{w}^T \frac{\mathbf{w}}{\|\mathbf{w}\|} f(x(s))=wTx(p)+b+rwT∥w∥w
代入(3),
f ( x ( s ) ) = 0 + r w T w ∥ w ∥ f ( x ( s ) ) = 0 + r w T w ∥ w ∥ f ( x ( s ) ) = 0 + r ∥ w ∥ f ( x ( s ) ) = r ∥ w ∥ f(\mathbf{x}^{(s)})=0+r \, \mathbf{w}^T \frac{\mathbf{w}}{\|\mathbf{w}\|}\\ f(\mathbf{x}^{(s)})= 0+r \frac{\mathbf{w}^T\mathbf{w}}{\|\mathbf{w}\|}\\ f(\mathbf{x}^{(s)})=0 + r \|\mathbf{w}\| \\f(\mathbf{x}^{(s)})= r \|\mathbf{w}\| f(x(s))=0+rwT∥w∥wf(x(s))=0+r∥w∥wTwf(x(s))=0+r∥w∥f(x(s))=r∥w∥
由此,
r = f ( x ( s ) ) ∥ w ∥ r = \frac{f(\mathbf{x}^{(s)})}{\|\mathbf{w}\|} r=∥w∥f(x(s))
解释: r r r 表示点 x ( s ) \mathbf{x}^{(s)} x(s) 到边界的有符号距离, w \mathbf{w} w 是法向量, w ^ \hat{\mathbf{w}} w^ 是单位法向量。
举一个实例
r r r 的距离是如何计算出来的?
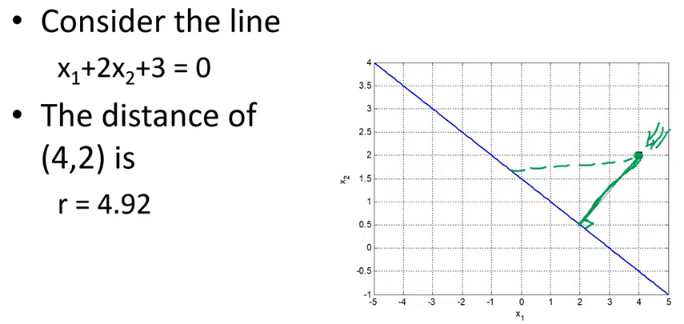
r = f ( x ( s ) ) ∥ w ∥ = 4 + 2 ∗ 2 + 3 1 2 + 2 2 = 11 5 ≈ 4.92 r = \frac{f(\mathbf{x}^{(s)})}{\|\mathbf{w}\|} = \frac{4+2*2+3}{\sqrt{1^2+2^2}} = \frac{11}{\sqrt{5}}\approx4.92 r=∥w∥f(x(s))=12+224+2∗2+3=511≈4.92
支持向量机的另一个视角

Hinge Loss: l ( f ( x ) , y ) = max ( 0 , 1 − y f ( x ) ) l(f(x), y) = \max(0, 1 - y f(x)) l(f(x),y)=max(0,1−yf(x))
基于链式损失函数限制:
y ⋅ f ( x ) ≥ 1 y \cdot f(x) \geq 1 y⋅f(x)≥1
对于正类( y = + 1 y=+1 y=+1):
f ( x ) ≥ 1 f(x) \geq 1 f(x)≥1
对于负类( y = − 1 y=-1 y=−1):
f ( x ) ≤ − 1 f(x) \leq -1 f(x)≤−1
恰好在间隔边界上的支持向量满足:
y ⋅ f ( x ) = 1 y \cdot f(x) = 1 y⋅f(x)=1
因此正类支持向量:
f ( x ( s ) ) = 1 f(x^{(s)}) = 1 f(x(s))=1
代入得到:
r = f ( x ( s ) ) ∥ w ∥ r = \frac{f(\mathbf{x}^{(s)})}{\|\mathbf{w}\|} r=∥w∥f(x(s))
r = 1 ∥ w ∥ r = \frac{1}{\lVert \mathbf{w} \rVert} r=∥w∥1
SVM(支持向量机)优化问题的两种等价形式
无约束优化问题 (Unconstrained Optimization Problem)
min w 1 2 w ⊤ w + C N ∑ i = 1 N max { 0 , 1 − y i f ( x i ; w ) } \min_{w}\;\; \frac{1}{2} w^{\top} w \;+\; \frac{C}{N}\sum_{i=1}^{N} \max\!\{0,\; 1 - y_i\, f(x_i; w)\} wmin21w⊤w+NCi=1∑Nmax{0,1−yif(xi;w)}
有约束优化问题 (Constrained Optimization Problem)
min w , ξ 1 2 w ⊤ w + C N ∑ i = 1 N ξ i s.t. y i f ( x i ; w ) ≥ 1 − ξ i , i = 1 , … , N , ξ i ≥ 0. \begin{aligned} \min_{w,\,\xi}\;\; & \frac{1}{2}\, w^{\top} w \;+\; \frac{C}{N}\sum_{i=1}^{N} \xi_i \\ \text{s.t.}\;\; & y_i\, f(x_i; w) \;\ge\; 1 - \xi_i,\quad i=1,\dots,N,\\ & \xi_i \;\ge\; 0. \end{aligned} w,ξmins.t.21w⊤w+NCi=1∑Nξiyif(xi;w)≥1−ξi,i=1,…,N,ξi≥0.
对应关系
ξ i = max { 0 , 1 − y i f ( x i ; w ) } \xi_i \;=\; \max\{0,\; 1 - y_i\, f(x_i; w)\} ξi=max{0,1−yif(xi;w)}
Note: 边距最大化 = 正则化