2024年全国研究生数学建模竞赛华为杯
C题 数据驱动下磁性元件的磁芯损耗建模
原题再现:
一、背景
随着国民经济发展和社会进步,基于电力电子技术的电能变换(电能变换是指将电能从一种形式转变成另一种形式,如直流电转换为不同电压的直流电,直流电转换为不同频率和大小的交流电等)得到迅速发展,尤其是新能源和信息通讯领域。电能变换技术在通讯电源、算力电源、数据中心电源、新能源功率变换、轨道交通、电动汽车、电气传动、智能电网、绿色照明等各个方面都有广泛应用。随着第三代功率半导体技术的发展,高频、高功率密度和高可靠性成为功率变换器产品的发展方向。磁性元件(变压器、电感等)作为功率变换器中必不可少的器件,担负着磁能的传递、存储、滤波等功能,对功率变换器的体积、重量、损耗、成本等都具有重要的影响。为了获得高效率和高功率密度的设计,除了满足磁性元件电气参数的可行性设计外,还要求其损耗小。因此,必须详细研究和分析磁性元件的损耗特性,磁性元件的损耗包括绕组损耗和磁芯损耗。铜导体的绕组损耗可以通过电磁场有限元仿真技术准确获得,但磁芯损耗是磁性材料在高频交变磁通作用下产生的功率损耗(本题中损耗都是指功率损耗),由于高频磁性材料(如铁氧体、合金磁粉芯、非晶/纳米晶等)本身的微观结构复杂,且其损耗与工作频率、磁通密度、励磁波形、工作温度、磁芯材料等诸多因素有关,并呈现复杂的非线性和相互关联性。现有的磁芯材料损耗模型与实际应用的需求有较大差异。
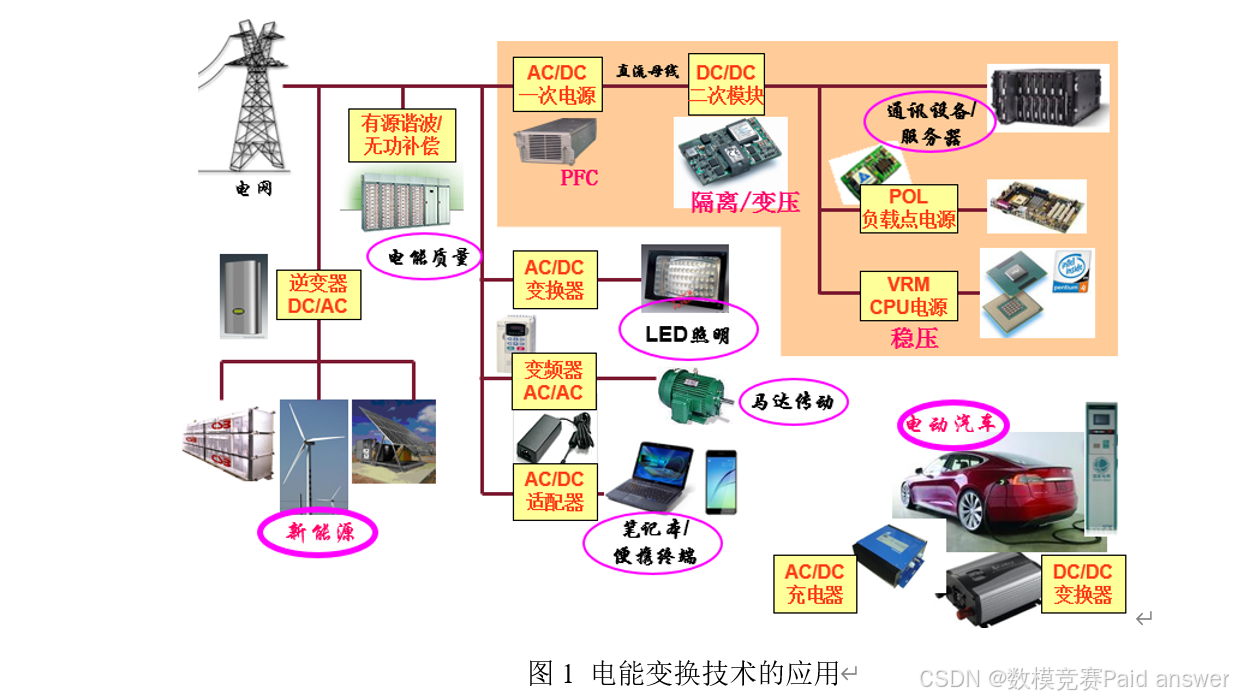

目前,磁芯损耗模型主要分为两大类:损耗分离模型和经验计算模型。
1.磁芯损耗分离模型
磁芯损耗可分成3个部分:磁滞损耗、涡流损耗和剩余损耗[1]。这种计算磁芯损耗的方法称为损耗分离模型,这种模型试图通过分别计算这些成分的损耗来得到总损耗。其计算公式如下:

2.磁芯损耗经验计算模型
经验计算模型则是一种更简便的方法,它基于实验数据或理论推导得出的经验公式来估算磁芯损耗。
斯坦麦茨方程(Steinmetz-equation(SE)[2])是最著名的经验计算模型之一。在正弦波励磁(励磁是指电流通过磁件的线圈产生磁场)下,磁芯损耗计算公式如下:
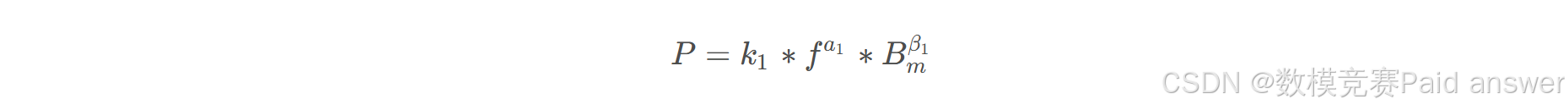
其中: P为磁芯损耗;f是频率; Bm是磁通密度的峰值; k1,α1,β1是根据实验数据拟合的系数,一般 , 。公式表明了单位体积的磁芯损耗(磁芯损耗密度)P取决于频率f和磁通密度峰值Bm的幂函数。SE方程仅适用于正弦波励磁,并且不同的磁芯材料和工况(工况指的是磁性材料所处的不同工作环境,包括温度、频率、励磁波形等),其系数 k1,α1,β1未必相同(更详细内容请参阅参考文献后备注1)。
由上述可以看出,磁芯损耗与温度、材料、频率、磁通密度的峰值有关系。但影响磁芯损耗的因素较多,现阶段,鲜有普遍适用并且精度高的模型,这使得业内在使用磁性元件时无法对磁芯损耗做出精确的评估,进而影响到对功率变换器效率的评估。因此,希望基于数据驱动,建立一个高精度并且普遍适用于各种工况的磁芯损耗模型成为亟待解决的问题(参考文献后有备注1:磁芯损耗模型的相关知识,及备注2:人工智能软件辅助答题规范,请注意参阅)。
二、问题描述
为解决磁性元件磁芯材料损耗精确计算问题,通过实测磁性元件在给定工况(不同温度、频率、磁通密度)下磁芯材料损耗的数据,通过数学建模(或算法)方法 ,建立功率磁性元件的磁芯材料损耗模型,并且将其预测磁性元件在其他工况中的磁芯损耗,检测模型精确度。
1. 实验场景和采集数据
磁芯损耗的测量目前一般采用交流功率法,如图3所示,被测磁芯一般采用圆环形(le是平均磁路长度;Ae是磁芯截面积),在磁芯上均匀绕制励磁绕组和感应绕组( N1和N2分别是励磁绕组和感应绕组的匝数,一般取 N1=N2 ),信号发生器产生给定频率 f(周期 T=1/f)的正弦波或者其他波形,经过高频功率放大器高频作为励磁源施加到励磁绕组上,根据安培环路定律,绕组励磁电流i(t)在磁芯上产生磁场强度 H(t)(磁场强度是指单位电流元在磁场中所受到的洛伦兹力,是描述磁场强弱的重要参数),磁场强度作用于导磁材料磁芯上产生磁通密度 (磁通密度是指单位面积垂直于磁力线的磁通量,即单位面积上垂直于磁场方向的磁通量),根据电磁感应定律,磁芯中交变的磁通则在感应绕组上产生感应电压u(t),进一步通过采集被测磁芯绕组的励磁电流i(t) ,从而得到磁场强度H(t)和磁通密度B(t) ,利用式(3)计算出励磁源的输出功率(单位体积),即磁芯损耗密度P。
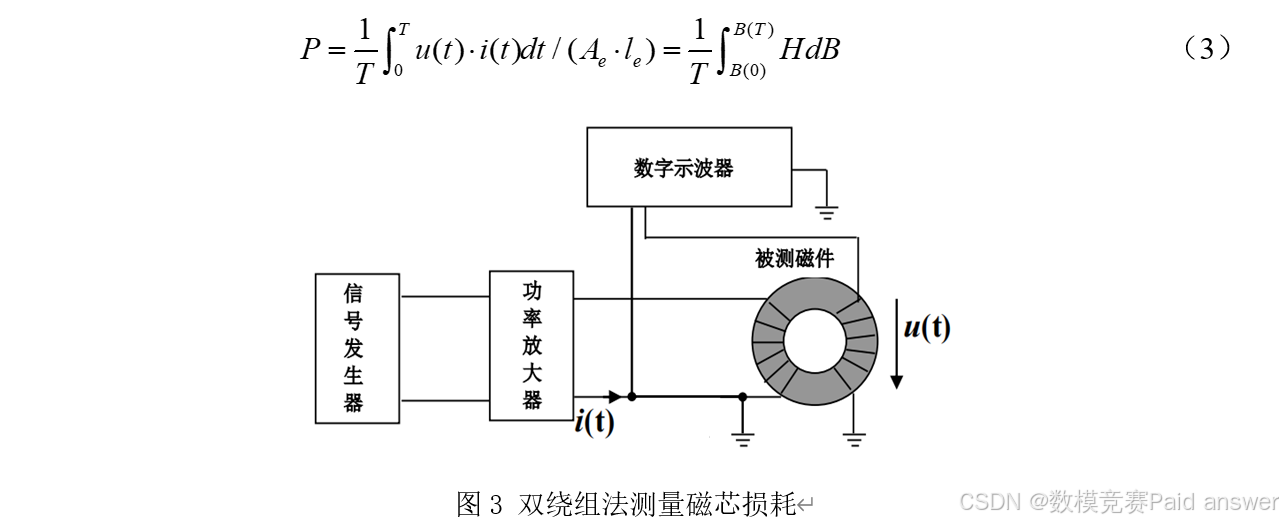
由式(3)也可知:一个励磁周期内的单位体积磁芯损耗就等于B-H磁滞回线的面积,如图4所示。
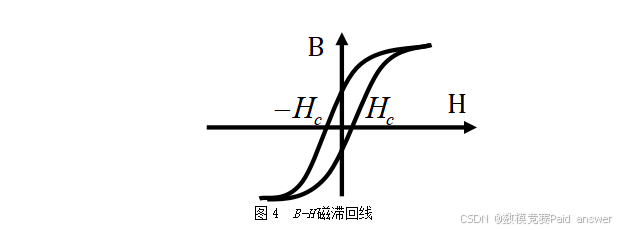
2. 数据说明
(1)解压附件(数据).rar,附件一为训练集,有4个数据表,分别表示来自4种不同磁芯材料所测的数据(由于磁芯材料的复杂性,我们仅用材料1、材料2、材料3、材料4来表示不同材料),4个数据表结构相同,其中:
第1列是温度,取4个值:25、50、70、90,单位:摄氏度;
第2列是频率,取值范围:50000—500000,单位:赫兹;
第3列是磁芯损耗,单位:每立方米瓦特;
第4列是励磁波形类型:正弦波、三角波和梯形波;
第5—1029列是磁通密度,共1024个采样点(一个周期时间内,相同间距采样),单位:特斯拉T;
每一行表示磁芯在一种工况下的实验结果,不同行表示不同的工况。
(2)附件二、附件三均为测试集,其中附件二:
第1列是样本序号;第2列是温度;第3列是频率;第4列是磁芯材料:材料1、材料2、材料3、材料4;第5—1029列是磁通密度(与附件一中相应的结构、格式、含义相同)。
附件三:第1列是样本序号;其他除磁芯损耗改为磁芯材料外,与附件一中相应的结构、格式、含义相同。
三、完成如下问题
问题一 励磁波形分类
励磁波形作为影响磁芯性能的核心要素之一,其形态深刻影响着磁芯的损耗特性。励磁波形的独特形状直接塑造了磁芯内部磁通的动态行为,不同的波形轮廓影响了磁通密度随时间的变化速率,导致其损耗特性呈现出显著差异。因此,准确识别出励磁波形,对于深入理解磁芯损耗机制、优化磁芯设计具有至关重要的价值。
励磁波形主要体现在磁通密度随时间变化的分布规律上,不同的励磁波形会导致磁通密度呈现出不同的增长、衰减或波动模式。请利用附件一中磁通密度数据,首先分析磁通密度的分布特征及不同波形的形状特征,提取出反映磁通密度分布及波形的形状特征变量;然后利用这些特征变量建立分类模型,识别出励磁的三种波形,分析分类模型的合理性及有效性;并对附件二中的样本识别出相应波形,把分类结果填入附件四(Excel表格)中第2列,要求:
(1)按样本序号填入相应分类结果,只填数字,1表示正弦波,2表示三角波,3表示梯形波,比如:附件二中第1个样品分类结果是三角波,在第2列样本序号为1对应行就填数字2;
(2)结果填入附件四后,保留原文件名,以附件材料上传;
(3)统计出附件二中三种波形的各自数量,呈现在论文正文中;
(4)特别把附件二中样本序号为:1、5、15、25、35、45、55、65、75、80的分类结果,以表格形式呈现在论文正文中。
问题二 斯坦麦茨方程(Steinmetz-equation)修正
在传统磁芯损耗模型中,斯坦麦茨方程(Steinmetz-equation)(公式(2))虽作为经典模型被广泛应用,却显著受限于其特定的适用条件,如:该方程主要针对正弦波形设计;对于不同种类的磁芯材料及工作温度的变化,SE方程会造成较大的误差,这在实际工程应用中带来了诸多不便与复杂性。目前已经有针对非正弦波形下磁芯损耗模型进行修正(见公式(7)、(8))。
请通过分析斯坦麦茨方程(公式(2)),在同一种磁芯材料、正弦波形下,对于不同温度变化,磁芯损耗预测效果存在的差异性,构造一种可适用于不同温度变化的磁芯损耗修正方程(即在原斯坦麦茨方程基础上,增加温度这个因素,以适应不同温度变化,使磁芯损耗预测效果更好);并以附件一材料1中正弦波形的数据为例,分析你构造的修正方程与斯坦麦茨方程,他们预测磁芯损耗的效果(误差)哪个更好?
问题三 磁芯损耗因素分析
在磁性元件的设计与优化领域,磁芯损耗是一个核心指标,其大小直接关系到设备的效率与稳定性。在众多影响磁芯损耗的因素中,温度、励磁波形以及磁芯材料被公认为是最常见且比较重要的三大要素。为了精准提升磁性元件的性能,我们亟需依托实验数据,深入剖析这三者如何独立或协同作用于磁芯损耗,并探索实现最低损耗的最优条件。
请根据附件一中的实验数据,通过数据分析技术,分析温度、励磁波形和磁芯材料这三个因素,是如何独立及协同影响着磁芯损耗(仅讨论两两之间协同影响);以及他们各自的影响程度;并给出这三个因素在什么条件下,磁芯损耗可能达到最小?
问题四 基于数据驱动的磁芯损耗预测模型
在磁芯损耗的研究领域中,尽管存在着众多传统模型(如文首“背景”所述),这些模型各自在不同的条件下展现了一定的应用价值,但普遍面临精度不足或适用范围受限的挑战。当前,业界缺乏一个既广泛适用又能提供高精度预测结果的磁芯损耗模型,这直接制约了磁性元件设计中对损耗的精确评估,进而影响了整体功率变换器效率的有效预估。鉴于这一现状,业界对构建更为便捷、精准的数据驱动模型寄予了厚望,旨在开发出一个能够跨越不同材料类型与工况条件的磁芯损耗预测模型。这样的模型将极大提升磁性元件设计的精确性与效率,为电力电子技术的进一步发展奠定坚实基础。
请利用附件一中的实验数据,通过数据分析与建模技术,构建磁芯损耗预测模型,分析模型的预测精度、泛化能力,以及对业界的各种指导意义;同时对附件三中样本的磁芯损耗进行预测,把预测结果填入附件四(Excel表格)中第3列,要求:(1)按样本序号填入相应的磁芯损耗预测结果,只保留小数点后1位;(2)结果填入附件四后,保留原文件名,(与问题一的结果一起)以附件材料上传;(3)特别把附件三中样本序号为:16、76、98、126、168、230、271、338、348、379的磁芯损耗预测结果,以表格形式呈现在论文正文中。
问题五 磁性元件的最优化条件
在磁性元件的设计与优化领域内,磁芯损耗固然是一个不容忽视的核心评价指标,但在工程实践中,为了实现磁性元件整体性能的卓越与最优化,需要综合考虑多个评价指标,其中,传输磁能就是重要的评价指标之一,因此,同时考虑磁芯损耗与传输磁能这二个评价指标,对于指导磁性元件的设计方向、优化其性能表现,具有重要的理论及实践意义。
请以问题四构建的磁芯损耗预测模型为目标函数,同时考虑传输磁能这个重要指标(由于传输磁能概念的复杂性,我们仅以频率与磁通密度峰值的乘积来衡量传输磁能大小),利用附件一中的实验数据,建立优化模型,分析在什么条件下(温度、频率、波形、磁通密度峰值及磁芯材料),能达到最小的磁芯损耗以及具有最大的传输磁能(即f∗Bm 达到最大)?
整体求解过程概述(摘要)
磁性元件(如变压器、电感)是功率变换器中不可或缺的核心器件,广泛应用于轨道交通、电动汽车、信息通讯等领域。在设计磁性元件时,除了电气参数需要符合要求外,还要求磁性材料在高频交变磁通下的磁芯损耗较低。然而,目前尚无一种高精度且通用的损耗预测模型能够满足实际应用需求。为此,本文构建了一种基于数据驱动的磁芯损耗模型,并进一步探索磁性元件损耗特性。
针对问题一,为提取反映磁通量密度分布的波形形状特征,我们从两个角度进行特征提取。首先,通过统计特征分析,选取波形的峰度、偏度等 8 种统计特征;其次,通过几何特征分析,利用可视化探索几何分布,并筛选出 11 种数学表征的几何特征。接着,基于决策树和随机森林算法计算特征的重要性,最终选取峰度、幅度前 k 大的频率和幅度为有效特征,并进行相关性分析。为提高模型预测的健壮性,选择决策树、随机森林和逻辑回归模型,分别对全部特征和筛选特征进行训练与测试,最终通过投票法确定分类结果,并对附件二中的数据进行预测。
针对问题二,题目要求对原始斯坦麦茨方程进行修正,构造可适用于不同温度下的磁芯损耗预测方程。对此,我们首先分析原始斯坦麦茨方程,经过对数变换后通过最小二乘法求解参数。我们结合统计误差分析和可视化数据分析,提出温度对磁芯损耗的线性/非线性影响假设。我们将温度作为线性项/对数变换项对斯坦麦茨方程进行修正,提出了 6种修正方程假设。经过模型参数求解和测试后,我们找出了拟合效果最好的修正方程,并对其在材料 1、正弦波下与原始斯坦麦茨方程的预测效果进行比较和分析。修正方程的误差相比原始斯坦麦茨方程显著减少,降低近 4 倍,R^2从 0.929979 提升至 0.985661。
针对问题三,要求分析温度、励磁波形、磁芯材料三种离散因素对磁芯损耗的影响。为满足方差齐性和正态性假设,我们对损耗数据进行了对数变换,使其更接近正态分布。对于三种因素下的 48 种组合方案,我们按频率排序,并采用分层随机抽样法随机抽取 50条数据。然后,通过单因素和双因素方差分析,评估各因素及其两两交互对磁芯损耗的影响。利用热力图和数据可视化分析,在低频条件下,材料 4、正弦波、90℃的组合表现出最低损耗;而在高频条件下,材料 4、正弦波、70℃为最优组合。
针对问题四,为设计通用的磁芯损耗预测模型,我们首先基于问题二中的修正斯坦麦茨方程,引入 one-hot 编码和等效正弦波频率对其进一步改进。尽管验证结果未取得理想效果,但为后续改进提供了重要思路。鉴于特征间存在复杂的非线性关系,我们采用了机器学习方法,构建了 9 种不同的机器学习模型,对温度、频率、波形、材料和磁通密度峰值五个主要特征进行训练,验证结果显示效果良好。为了进一步提升模型性能,我们增加了问题一中提取的峰值特征来描述磁通密度分布,验证表明模型拟合效果得到了进一步改进。随后,我们引入了基于磁通密度变化率(𝒅B(t)/dt)的 IGSE 预测模型,并通过模型堆叠的方式,将 IGSE 计算结果作为先验知识进行训练。此方法结合了可解释性与非线性学习能力,最终 CatBoost 模型在此特征组合上取得了最佳预测效果,取得平均相对误差0.03542。
针对问题五,为解决在实现最小磁芯损耗的同时最大化传输磁能(频率与磁通密度峰值的乘积)的双目标优化问题,我们结合问题三中的分析结果,设定最低磁芯损耗条件:材料 4、正弦波、70℃或 90℃。我们采用遗传算法、粒子群优化算法和灰狼优化算法,结合问题四中基于五种基本特征训练的 CatBoost 模型进行优化求解。结果表明,在频率约188,000 Hz、温度 90℃、正弦波、磁通密度峰值为 0.012、材料四的条件下,灰狼优化算法表现出最优解。为确保结果的严谨性,我们进一步使用灰狼优化算法对 48 种离散变量组合进行了优化实验,验证了其稳健性和效果。
模型假设:
假设 1:本题附件中提供的所有关于磁芯损耗相关数据全部真实有效;
假设 2:本题附件中的所有数据不存在异常值和缺失值,并且定类数据标注无误。
假设 3:在一定的温度条件下,实验所用材料的内部结构与外部形态不会发生变化
假设 4:本题附件中不同样本表示不同工况下的数据结果,样本之间都相互独立。
问题分析:
根据问题一的要求,需要深入理解磁通密度的分布特征和不同波型的形状特征提取出能够反映磁通密度分布和波型形状特征的变量,建立模型准确识别出励磁波型类型。观察附件一中的训练数据,每个样本磁通密度分布通过一组数量为 1024 的浮点类型数据进行表示,并且每个样本均标明所属的波型类型。
首先,我们从两个角度选取反映磁通密度分布和波型形状的特征:
1) 统计特征提取:通过计算一组数据的基本统计量,如最大值、最小值、均值、方差、偏度和峰度等,来描述数据的集中趋势和离散程度。
2) 几何特征分析:通过可视化方法来探索数据的分布形态特征,通过观察图形的形状、对称性和集中程度,识别潜在的特征。汇总以上两个角度选取的特征,整合样本波型类型作为标签,利用五折交叉验证方法将附件一中的全部样本划分为训练集和测试集,作为后续训练和测试分类模型的输入。为了更好的选取合适的特征,我们使用决策树模型和随机森林模型对特征重要性进行评价,判断挑选的特征对决策的影响。最后,根据题目要求我们对选取的有效特征尝试进行机理分析,总结经验并填写题目要求的相应结果表格。
根据题目要求,我们需要对现有的斯坦麦茨方程进行分析,探究不同温度下对方程预测效果的影响。题目明确告知以下信息:1. 斯坦麦茨方程主要针对正弦波形设计;2. 对于不同种类的磁芯材料及工作温度的变化,斯坦麦茨方程会造成较大的误差。因此我们解决本题的思路是:1. 数据分析和预处理;2. 首先分析目前斯坦麦茨方程,尝试理解并根据数据集求解参数;3. 对数据进行可视化,不同材料下温度对斯坦麦茨方程的影响,提出改进方程的可行方式假设;4. 不断对假设进行验证,分析改进方程对数据的拟合情况并提出新的假设,往复尝试并验证结果;5. 对不同改进方法的预测效果进行综合分析,总结经验为后续问题服务。
磁芯损耗是磁性元件设计与优化中的关键指标,直接影响设备的效率和稳定性。温度、励磁波形及磁芯材料是影响磁芯损耗的三大主要因素。本题旨在分析这三者对磁芯损耗的独立及协同影响,特别是探讨两两因素之间的交互作用,并找到在什么条件下磁芯损耗可能最小。通过对实验数据进行统计分析和建模,可以得到以下主要问题:
1. 温度、励磁波形和磁芯材料各自对磁芯损耗的影响程度如何?
2. 两两因素之间是否存在协同作用?如果有,这些交互作用如何影响磁芯损耗?
3. 在什么组合条件下,磁芯损耗可能达到最小?
本研究拟采用以下方法对数据进行分析:
1. 单因素方差分析:用于评估每个因素(温度、励磁波形、磁芯材料)对磁芯损耗的独立影响。通过比较不同水平的均值,判断该因素的影响显著性。
2. 双因素方差分析:用于评估两两因素之间的交互作用(例如温度与励磁波形、温度与磁芯材料、励磁波形与磁芯材料)。通过交互项的显著性分析来判断协同效应是否显著。
在磁芯损耗研究中,虽然已有众多传统模型存在,但它们往往在精度和适用范围上面临挑战,限制了对磁性元件设计中损耗的精确评估。因此,本题的核心要求旨在构建一个基于数据驱动的通用预测方法,构建能够在不同材料类型和工况条件下进行有效预测的磁芯损耗模型。这一模型的建立将有助于提高磁性元件设计的精确性与效率,进一步推动电力电子技术的发展。
在磁性元件的设计与优化中,磁芯损耗和传输磁能是两个重要的评价指标。为了实现整体性能的卓越与最优化,本研究将建立一个双目标优化模型,旨在同时最小化磁芯损耗和最大化传输磁能(频率与磁通密度峰值的乘积)。
模型的建立与求解整体论文缩略图



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序代码如下:
import pandas as pd
import numpy as np
data = pd.read_csv("./data/train_2.csv")
print(data.shape)
selectColumns = data[[str(i) for i in range(1024)]]
for j in range(2000,2500):
temp = selectColumns.iloc[j].to_numpy()
# 进行 FFT
fft_result = np.fft.fft(temp)
frequencies = np.fft.fftfreq(len(temp))
# 只取正频率部分
positive_frequencies = frequencies[:len(frequencies)//2]
fft_magnitude = np.abs(fft_result[:len(fft_result)//2])
# 归一化到 [0, 1] 之间
fm_min = np.min(fft_magnitude)
fm_max = np.max(fft_magnitude)
fft_magnitude = (fft_magnitude - fm_min) / (fm_max - fm_min)
data_X = []
data_Y = []
for i in range(len(positive_frequencies)):
if fft_magnitude[i] > 0.01:
data_X.append(positive_frequencies[i])
data_Y.append(fft_magnitude[i])
print(j,len(data_Y),data.iloc[j, 3])
import matplotlib.pyplot as plt
import pandas as pd
import math
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error, r2_score
# 读取数据
data = pd.read_csv("./data/train_4.csv")
# 初始化列表
X, Y, Z, T, XY, XT, YT, TT = [], [], [], [], [], [], [], []
# 数据处理
for d in data.iloc:
if d[3] != "正弦波":
continue
P = d[2]
f = d[1]
tt = d[0]
B = max([abs(i) for i in d[4:1028]])
logP = math.log(P)
logf = math.log(f)
logB = math.log(B)
logT = tt
X.append(logf)
Y.append(logB)
XY.append(logf*logB)
T.append(logT)
XT.append(logT*logf)
YT.append(logT*logB)
Z.append(logP)
x = np.array(X)
y = np.array(Y)
xy = np.array(XY)
t = np.array(T)
xt = np.array(XT)
yt = np.array(YT)
z = np.array(Z)
# 将 x, y, t 组合成一个特征矩阵
XMat = np.column_stack((x, y, t, xt, yt))
# K 折交叉验证
kf = KFold(n_splits=5, shuffle=True, random_state=42)
mse_list = [] # 存储每折的均方误差
mse_exp_list = []
r2_list = [] # 存储每折的 R^2 分数
r2_exp_list = []
for train_index, test_index in kf.split(XMat):
X_train, X_test = XMat[train_index], XMat[test_index]
y_train, y_test = z[train_index], z[test_index]
# 创建线性回归模型
model = LinearRegression()
# 拟合模型
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算均方误差和 R^2 分数
mse = mean_squared_error(y_test, y_pred)
mse_exp = mean_squared_error(np.exp(y_pred), np.exp(y_test))
r2 = r2_score(y_test, y_pred)
r2_exp = r2_score(np.exp(y_pred), np.exp(y_test))
mse_list.append(mse)
mse_exp_list.append(mse_exp)
r2_list.append(r2)
r2_exp_list.append(r2_exp)
# 计算平均均方误差和平均 R^2 分数
mean_mse = np.mean(mse_list)
mean_mse_exp = np.mean(mse_exp_list)
mean_r2 = np.mean(r2_list)
mean_r2_exp = np.mean(r2_exp_list)
# 提取最后一折的参数
final_model = LinearRegression()
final_model.fit(XMat, z) # 使用整个数据集训练
a = final_model.coef_[0]
b = final_model.coef_[1]
c = final_model.coef_[2]
d = final_model.coef_[3]
e = final_model.coef_[4]
k = final_model.intercept_
# 输出结果
print(f"参数 a: {a}, b: {b}, c: {c}, d: {d}, e: {e}, k: {k}")
print(f"平均均方误差: {mean_mse}")
print(f"平均均方误差 EXP: {mean_mse_exp}")
print(f"平均 R^2 分数: {mean_r2}")
print(f"平均 R^2 分数 EXP: {mean_r2_exp}")
# 对整个训练集进行训练
z_pred = final_model.predict(XMat) # 使用模型预测整个训练集
# 创建三维图形
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=4, azim=-15)
# 绘制真实值的三维散点图
scatter_real = ax.scatter(x, y, z, c='#D64161', alpha=0.2, marker='.')# 绘制预测值的三维散点图
scatter_pred = ax.scatter(x, y, z_pred, c='#8A2BE2', alpha=0.5, marker='.')
# 设置坐标轴标签
ax.set_xlabel('log(f)')
ax.set_ylabel('log(B)')
ax.set_zlabel('log(P)')
ax.set_xticks([11, 11.5, 12, 12.5]) # X 轴刻度
ax.set_yticks([-2, -3, -4]) # Y 轴刻度
ax.set_zticks([8, 10, 12, 14]) # Z 轴刻度
ax.set_xlabel('log(f)', fontsize=14, labelpad=10)
ax.set_ylabel('log($B_m$)', fontsize=14, labelpad=10)
ax.set_zlabel('log(P)', fontsize=14, labelpad=10)
plt.savefig("./q2_opt4.png", dpi=300)
# 显示图形
plt.show()
import math
import numpy as np
import pandas as pd
from catboost import CatBoostRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from scipy.stats import kurtosis, skew
# 读取数据
data1 = pd.read_csv("data/train_1.csv")
data1['材料'] = '材料 1'
data2 = pd.read_csv("data/train_2.csv")
data2['材料'] = '材料 2'
data3 = pd.read_csv("data/train_3.csv")
data3['材料'] = '材料 3'
data4 = pd.read_csv("data/train_4.csv")
data4['材料'] = '材料 4'
data = pd.concat([data1, data2, data3, data4])
# 特征处理函数
def checkFeature0(t):
return [1 if t == x else 0 for x in [25, 50, 70, 90]]
def checkFeatureMaterial(data):
return [1 if data == f'材料{i+1}' else 0 for i in range(4)]
def checkFeature3(t):
return [1 if t == wave else 0 for wave in ['正弦波', '三角波', '梯形波']]# 处理数据
dataX = []
dataY = []
for index, row in data.iterrows():
feature = []
feature.append(math.log(row[0])) # 温度
feature.append(math.log(row[1])) # 频率
feature.extend(checkFeature3(row[3])) # 波形
feature.extend(checkFeatureMaterial(row['材料'])) # 材料特征向量maxB = max(abs(i) for i in row[4:1028])
peak_kurtosis = kurtosis(row[4:1028].to_numpy().astype(np.float32))peak_skewness = skew(row[4:1028].to_numpy().astype(np.float32))
feature.append(maxB) # B 最大值
dataX.append(feature)
dataY.append(math.log(row[2]))
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(dataX, dataY, test_size=0.3,random_state=42)
# 创建 CatBoost 回归器
catboost_model = CatBoostRegressor(iterations=1000, depth=6, learning_rate=0.1,loss_function='RMSE', verbose=0)
# 训练模型
catboost_model.fit(X_train, y_train)
# 预测
y_pred = catboost_model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
tss = np.mean((y_test - np.mean(y_test)) ** 2)
r2 = 1 - (mse / tss)