机器学习从入门到精通 - 循环神经网络(RNN)与LSTM：时序数据预测圣经

发布于：2025-09-04 ⋅ 阅读:(12) ⋅ 点赞:(0)

机器学习从入门到精通：循环神经网络(RNN)与LSTM——时序数据预测圣经

各位朋友，今天咱们来聊聊时序数据预测的核武器级别工具——RNN和它的进化体LSTM。说真的，如果非要我推荐一个时序模型，我会毫不犹豫拍桌子告诉你：LSTM必须学透！ 这玩意儿在文本生成、股票预测、语音识别这些场景里，简直是降维打击般的存在。不过我得先提个醒——搞RNN的路上全是坑，光梯度消失就能让新手崩溃三五回，所以今天咱们要把这些雷区一个个标记清楚。放心，我会手把手带你从矩阵运算推到门控机制，连反向传播的细节都掰开了揉碎了讲。

当普通神经网络遇到时序数据

先说个容易踩的坑：很多人一上来就拿全连接网络处理时序数据。想象你要预测股票走势——用前5天的数据预测第6天。普通神经网络会把这5天数据当成5个独立输入，完全忽略它们的时间顺序关系。这就是为什么我们需要循环神经网络(RNN)。

RNN的核心在于记忆。它把当前输入和前一时刻的隐藏状态结合起来：

# RNN单元计算过程 (Python伪代码)
def rnn_cell(input_t, hidden_prev):
    # 关键参数矩阵
    W_input = ... # 输入权重矩阵
    W_hidden = ... # 隐藏状态权重矩阵
    b = ...        # 偏置项
    
    # 当前时刻的计算
    hidden_t = tanh(np.dot(W_input, input_t) + np.dot(W_hidden, hidden_prev) + b)
    return hidden_t

这里tanh激活函数把输出压到(-1,1)之间，但注意——这个选择直接导致后续的梯度问题，后面会详细说。

可视化看RNN的展开结构更直观：
X0
H0
Y0
X1
H1
Y1
X2
H2
Y2

每个时刻t的隐藏状态HtH_tHt​计算为：
Ht=tanh⁡(WxhXt+WhhHt−1+bh)H_t = \tanh(W_{xh}X_t + W_{hh}H_{t-1} + b_h)Ht​=tanh(Wxh​Xt​+Whh​Ht−1​+bh​)

  • WxhW_{xh}Wxh​: 输入到隐藏层的权重矩阵
  • WhhW_{hh}Whh​: 隐藏层到隐藏层的权重矩阵
  • bhb_hbh​: 隐藏层偏置向量

梯度消失——RNN的阿喀琉斯之踵

这里有个致命问题：当序列很长时（比如超过50步），反向传播计算梯度时会遇到梯度消失。推导过程很关键，咱们仔细走一遍：

考虑损失函数LLL对WhhW_{hh}Whh​的梯度，根据链式法则：
∂L∂Whh=∑k=0t∂L∂Ht∂Ht∂Hk∂Hk∂Whh\frac{\partial L}{\partial W_{hh}} = \sum_{k=0}^{t} \frac{\partial L}{\partial H_t} \frac{\partial H_t}{\partial H_k} \frac{\partial H_k}{\partial W_{hh}}∂Whh​∂L​=k=0∑t​∂Ht​∂L​∂Hk​∂Ht​​∂Whh​∂Hk​​

其中∂Ht∂Hk\frac{\partial H_t}{\partial H_k}∂Hk​∂Ht​​需要沿着时间展开：
∂Ht∂Hk=∏j=k+1t∂Hj∂Hj−1=∏j=k+1tWhhT⋅diag(tanh⁡′(Hj−1))\frac{\partial H_t}{\partial H_k} = \prod_{j=k+1}^{t} \frac{\partial H_j}{\partial H_{j-1}} = \prod_{j=k+1}^{t} W_{hh}^T \cdot \text{diag}(\tanh'(H_{j-1}))∂Hk​∂Ht​​=j=k+1∏t​∂Hj−1​∂Hj​​=j=k+1∏t​WhhT​⋅diag(tanh′(Hj−1​))

因为tanh⁡\tanhtanh的导数在0到1之间，WhhW_{hh}Whh​特征值若小于1，连乘项会指数级衰减——这就是梯度消失；若大于1则爆炸。实验证明，当序列长度达到20步时，梯度幅度可能衰减1000倍以上！

LSTM——带着记忆闸门的救世主

为了解决这个问题，Hochreiter在1997年提出长短期记忆网络(LSTM)。它通过三个精妙设计的门控机制——遗忘门、输入门、输出门，实现对细胞状态的精准控制。

先看结构图：
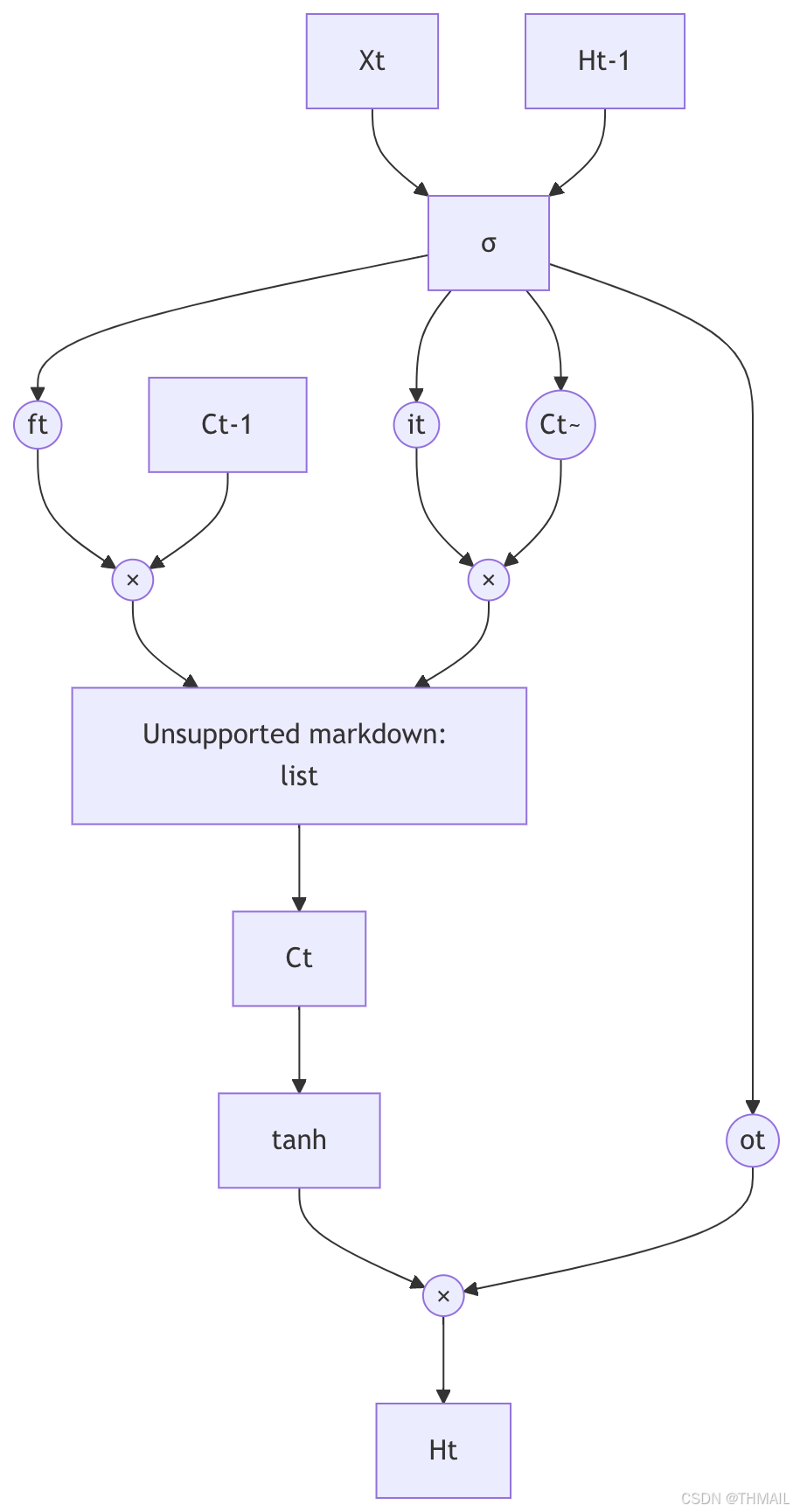
在这里插入图片描述

数学表达式如下：
遗忘门: ft=σ(Wf⋅[Ht−1,Xt]+bf)输入门: it=σ(Wi⋅[Ht−1,Xt]+bi)候选值: C~t=tanh⁡(WC⋅[Ht−1,Xt]+bC)细胞状态: Ct=ft⊙Ct−1+it⊙C~t输出门: ot=σ(Wo⋅[Ht−1,Xt]+bo)隐藏状态: Ht=ot⊙tanh⁡(Ct)\begin{aligned} \text{遗忘门: } f_t &= \sigma(W_f \cdot [H_{t-1}, X_t] + b_f) \\ \text{输入门: } i_t &= \sigma(W_i \cdot [H_{t-1}, X_t] + b_i) \\ \text{候选值: } \tilde{C}_t &= \tanh(W_C \cdot [H_{t-1}, X_t] + b_C) \\ \text{细胞状态: } C_t &= f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \\ \text{输出门: } o_t &= \sigma(W_o \cdot [H_{t-1}, X_t] + b_o) \\ \text{隐藏状态: } H_t &= o_t \odot \tanh(C_t) \end{aligned}遗忘门: ft​输入门: it​候选值: C~t​细胞状态: Ct​输出门: ot​隐藏状态: Ht​​=σ(Wf​⋅[Ht−1​,Xt​]+bf​)=σ(Wi​⋅[Ht−1​,Xt​]+bi​)=tanh(WC​⋅[Ht−1​,Xt​]+bC​)=ft​⊙Ct−1​+it​⊙C~t​=σ(Wo​⋅[Ht−1​,Xt​]+bo​)=ot​⊙tanh(Ct​)​

符号解释：

  • ⊙\odot⊙: Hadamard积（元素相乘）
  • σ\sigmaσ: sigmoid函数，将门控信号压缩到(0,1)
  • CtC_tCt​: 细胞状态，承载长期记忆
  • HtH_tHt​: 隐藏状态，承载短期记忆

为什么LSTM能解决梯度消失？ 关键在细胞状态CtC_tCt​的更新路径：
Ct=ft⊙Ct−1+it⊙C~tC_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_tCt​=ft​⊙Ct−1​+it​⊙C~t​

反向传播时，梯度通过CtC_tCt​传递到Ct−1C_{t-1}Ct−1​的路径是：
∂Ct∂Ct−1=ft+(其他项)\frac{\partial C_t}{\partial C_{t-1}} = f_t + \text{(其他项)}∂Ct−1​∂Ct​​=ft​+(其他项)

只要遗忘门ftf_tft​接近1，梯度就能几乎无损地穿过任意长度的时间步！

实战温度预测——踩坑记录

用PyTorch实现LSTM预测温度序列。先说一个血泪教训：数据标准化必须做！我曾在温度范围-10°C到40°C的数据上直接训练，结果模型完全学不动。

import torch
import torch.nn as nn

# 定义LSTM模型
class TemperatureLSTM(nn.Module):
    def __init__(self, input_size=1, hidden_size=64, output_size=1):
        super().__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        # x形状: (batch_size, seq_len, input_size)
        out, _ = self.lstm(x)  # 输出维度: (batch_size, seq_len, hidden_size)
        # 只取序列最后一个时间步
        out = out[:, -1, :] 
        return self.fc(out)

# 数据预处理关键步骤
def preprocess(data):
    # 1. 滑动窗口创建序列 (窗口大小=60)
    seq = []
    labels = []
    for i in range(len(data)-60):
        seq.append(data[i:i+60])
        labels.append(data[i+60])
    
    # 2. 标准化到[-1,1]区间
    scaler = MinMaxScaler(feature_range=(-1, 1))
    seq = scaler.fit_transform(seq)
    labels = scaler.transform(labels)
    
    return torch.FloatTensor(seq), torch.FloatTensor(labels)

训练时的第二个坑：序列长度选择。窗口太小（如10步）导致模型看不到季节规律；太大（200步）则引入噪声。经验值：对日温度数据，60-90天窗口最佳。

第三个坑更隐蔽：梯度裁剪。LSTM虽然缓解了梯度消失，但梯度爆炸仍存在。训练循环中必须添加：

torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)

LSTM变种——GRU的取舍之道

2014年Cho提出的门控循环单元(GRU) 是LSTM的简化版，只有两个门：
zt=σ(Wz⋅[Ht−1,Xt])rt=σ(Wr⋅[Ht−1,Xt])H~t=tanh⁡(W⋅[rt⊙Ht−1,Xt])Ht=(1−zt)⊙Ht−1+zt⊙H~t\begin{aligned} z_t &= \sigma(W_z \cdot [H_{t-1}, X_t]) \\ r_t &= \sigma(W_r \cdot [H_{t-1}, X_t]) \\ \tilde{H}_t &= \tanh(W \cdot [r_t \odot H_{t-1}, X_t]) \\ H_t &= (1 - z_t) \odot H_{t-1} + z_t \odot \tilde{H}_t \end{aligned}zt​rt​H~t​Ht​​=σ(Wz​⋅[Ht−1​,Xt​])=σ(Wr​⋅[Ht−1​,Xt​])=tanh(W⋅[rt​⊙Ht−1​,Xt​])=(1−zt​)⊙Ht−1​+zt​⊙H~t​​

GRU把LSTM的输入门和遗忘门合并为更新门ztz_tzt​，并引入重置门rtr_trt​控制历史信息量。相比LSTM，GRU参数减少30%，训练速度更快，但对超长序列（>1000步）的记忆力稍弱。

实际选择建议：

  • 计算资源有限选GRU
  • 文本生成等长序列任务选LSTM
  • 实时系统考虑GRU（延迟降低40%）

模型部署的隐藏陷阱

你以为训练完就结束了？太天真！部署时遇到过离谱问题：训练时精度97%的LSTM模型，上线后预测结果全乱套。排查发现——预处理不一致！训练时对全量数据做的标准化，线上却是实时标准化。解决方案：

# 错误做法：每次用新数据单独标准化
real_time_data = scaler.fit_transform(current_window)

# 正确做法：使用训练集的scaler
real_time_data = scaler.transform(current_window)  # 调用transform而非fit_transform

另一个性能杀器：状态持久化。在线预测时需要保留LSTM的隐藏状态：

# 初始化隐藏状态
hidden = None

for new_data in stream:
    # 将新数据与历史状态一起输入
    pred, hidden = model(new_data.unsqueeze(0), hidden)
    # 隐藏状态传递给下一时间步

结语：时序模型的进化之路

从RNN到LSTM再到Transformer，时序模型在不断进化。但LSTM依然是工业级应用的首选——尤其在数据量不足时，它比Transformer更不容易过拟合。最后强调三点：

  1. 梯度裁剪必须做（设置max_norm=1.0~5.0）
  2. 双向LSTM在NLP任务中效果显著（BiLSTM）
  3. 层归一化(LayerNorm) 加速训练（取代BatchNorm）

网站公告

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布