打眼一看,毫无思路。
我又没学过 LCT 和可撤销并查集,怎么办?
(洛谷上有一些题解把问题复杂化了,于是有了我写的这篇)
题面指路:P4246 [SHOI2008] 堵塞的交通 - 洛谷
前置知识:线段树
解析:
1.先想想
首先,我们得明确要干什么:
添加相邻点之间的边
删除相邻点之间的边
查询两个节点的连通性
注意到只有两行要操作,不如直接枚举路径:
part 1:直接从 a 走到 b
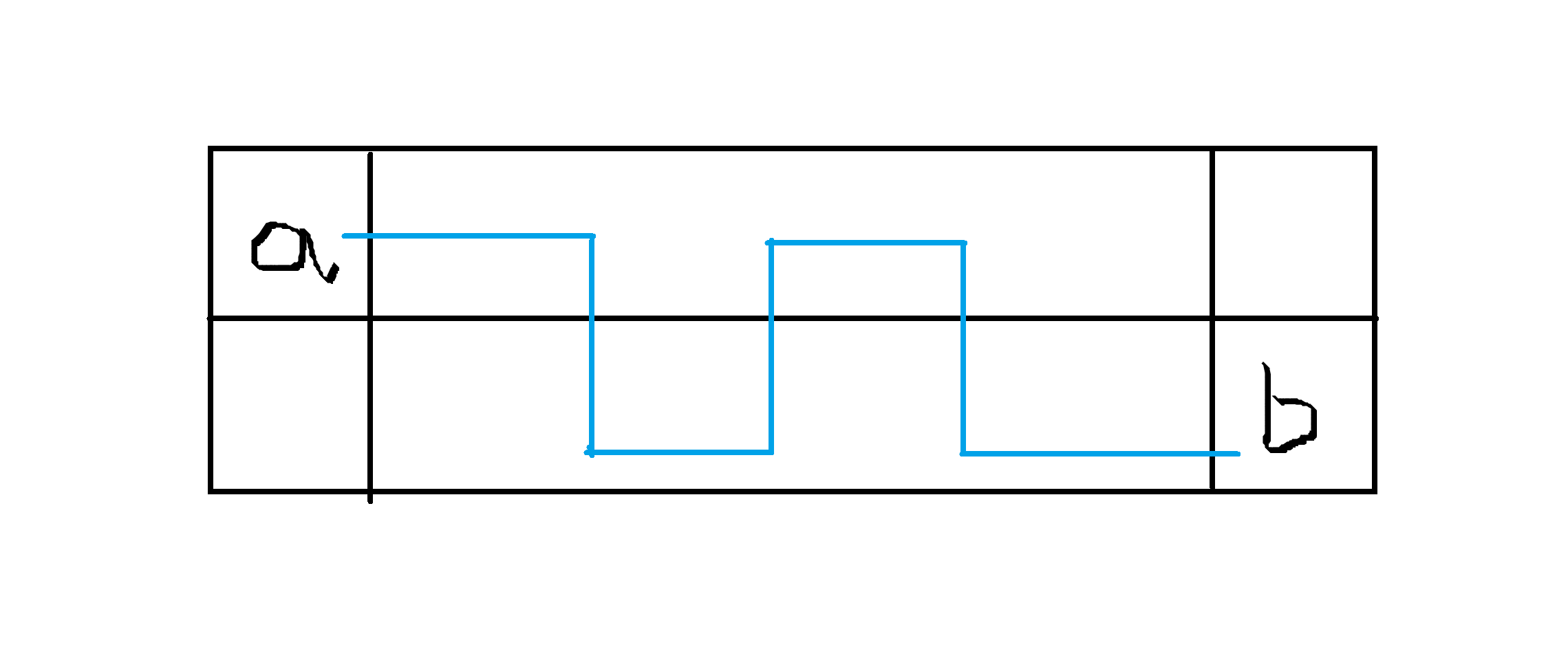
(实际可能没这么多弯弯绕绕,我为了好看这样画而已)
part 2:从 a 绕到左边的列再走回 b
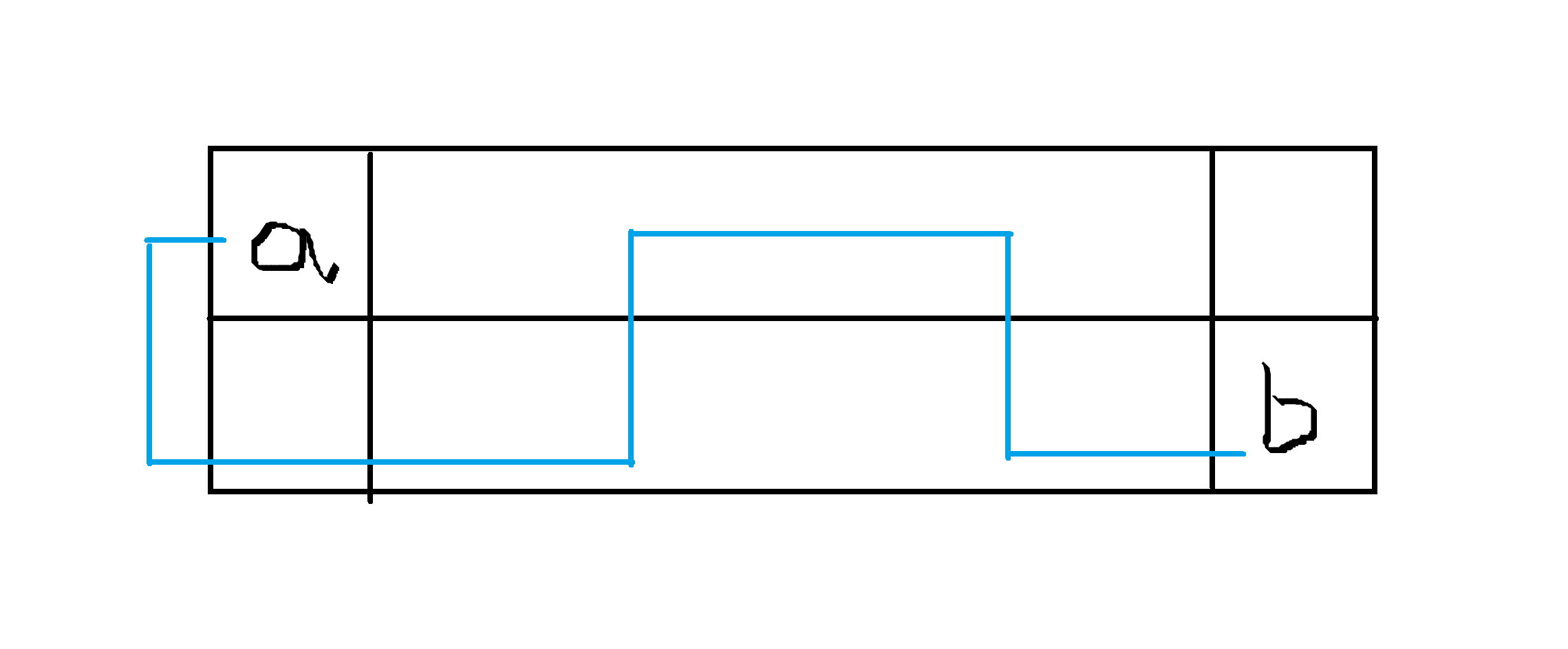
part 3:从 a 走到 b 右边的列再绕回来
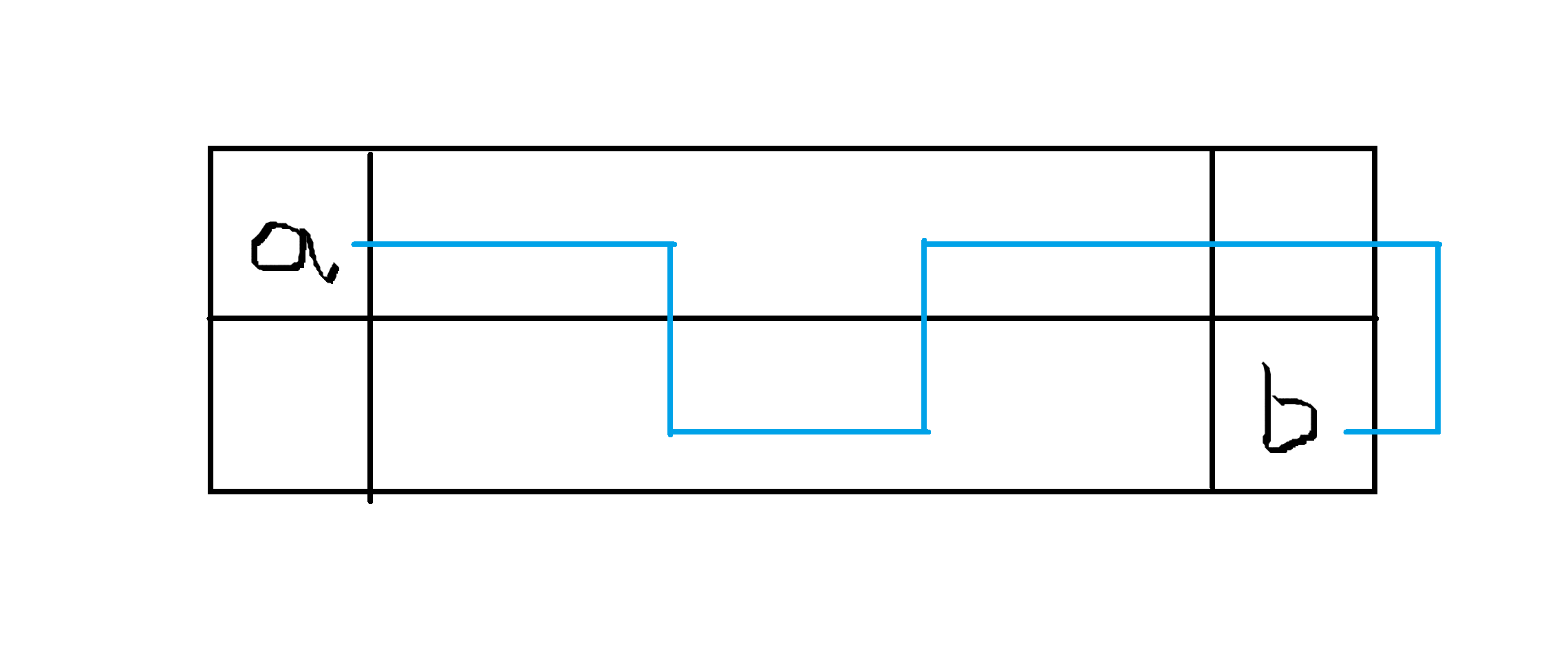
我们发现,这样可以把问题转化成区间连通性判断,
(比如说如果 a 到 k 联通,而 k 到 b 也联通,那么 a 到 b 联通)
而支持区间修改(添加和删除)的数据结构,自然想到了线段树。
2.状态设计
以下代码中出现的行默认是based - 0,即题目定义行 - 1。
以下注释中 l,r 叫端点,线段树里的叫节点。
考虑设计线段树节点结构体:
#define lc(p) (p << 1)
#define rc(p) (p << 1 | 1) //我自己喜欢用的左右子节点的宏定义
const int N = 1e5 + 10;
//线段树端点
struct node {
int l, r; //左右端点
int cnt[3][3]; // connect[0/1][0/1]:左端点的 0/1 行和右端点的 0/1 行联通就为 1,反之为 0
int ra[3]; //roundabout[0]:从左端点的 0 行绕到区间的中间,再绕回来左端点的 1 行,两点联通为 1,反之为 0
//roundabout[1]:从右端点的 0 行绕到区间的中间,再绕回来右端点的 1 行,两点联通为 1,反之为 0
} tr[N << 2]; //线段树空间开 4 倍 建图的时候就这么建:
void build(int p, int l, int r) { //建树
tr[p].l = l; tr[p].r = r;
tr[p].cnt[0][1] = tr[p].cnt[1][0] = 0; //初始化
tr[p].ra[0] = tr[p].ra[1] = 0;
if (l == r) { // 当只有一列的时候
tr[p].cnt[0][0] = tr[p].cnt[1][1] = 1;
// 左端点的 0 行和右端点的 0 行联通,左端点的 1 行和右端点的 1 行联通
//反正就一列,一行就一个
return;
}
int mid = (l + r) >> 1;
build(lc(p), l, mid);
build(rc(p), mid + 1, r);
tr[p] = merge(tr[lc(p)], tr[rc(p)]); //这个函数下面会讲
}再设计 merge 更新 & 合并函数:
这个是本题最难的部分(其实也一般),不过我的注释很详细!
(以下用 & 连接起来的判断句,其中有一个为 0 整个都为 0)
int n, valc[N], valr[2][N];
// valc[x]:第 x 列上下联通
// valr[r][x]:第 r 行的 x - 1 列 和 x 列联通
// 因为给出修改的路径的都是相邻的,所以 valr 就很好用,详见主函数
// 合并函数
node merge(node le, node re) { // 输入左右节点
node res; // 新建合并后节点
res.l = le.l; res.r = re.r; // 新节点左右端点赋值
res.ra[0] = ( le.ra[0] | (le.cnt[0][0] & valr[0][re.l] & re.ra[0] & valr[1][re.l] & le.cnt[1][1]) );
// ra[0]:我们想从新节点的左端点的 0 行绕到区间的中间,再绕回来左端点的 1 行,两点联通
// 如果左节点 le 可以这么做,那就直接可以
// 否则要先从 le 左端点的 0 行到 le 右端点的 0 行,第 0 行再从 le 右端点到 re 左端点
// 判断右节点 re 的 ra[0],再从第 1 行的 re 左端点到 le 右端点,从 le 右端点的 1 行到 le 左端点的 1 行
res.ra[1] = ( re.ra[1] | (re.cnt[0][0] & valr[0][re.l] & le.ra[1] & valr[1][re.l] & re.cnt[1][1]) );
// ra[1]:我们想从新节点的右端点的 0 行绕到区间的中间,再绕回来右端点的 1 行,两点联通
// 如果右节点 re 可以这么做,那就直接可以
// 否则要先从 re 右端点的 0 行到 re 左端点的 0 行,第 0 行再从 re 左端点到 le 右端点
// 判断左节点 le 的 ra[1],再从第 1 行的 le 右端点到 re 左端点,从 le 左端点的 1 行到 le 右端点的 1 行
res.cnt[0][0] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][0]) );
// cnt[0][0]:我们想要新节点的左端点的 0 行和右端点的 0 行联通
// 如果左节点 le 的左端点的 0 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 0 行联通,那么就联通
// 如果左节点 le 的左端点的 0 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 0 行联通,那么就联通
res.cnt[0][1] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][1]) );
// cnt[0][1]:我们想要新节点的左端点的 0 行和右端点的 1 行联通
// 如果左节点 le 的左端点的 0 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 1 行联通,那么就联通
// 如果左节点 le 的左端点的 0 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 1 行联通,那么就联通
res.cnt[1][0] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][0]) );
// cnt[1][0]:我们想要新节点的左端点的 1 行和右端点的 0 行联通
// 如果左节点 le 的左端点的 1 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 0 行联通,那么就联通
// 如果左节点 le 的左端点的 1 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 0 行联通,那么就联通
res.cnt[1][1] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][1]) );
// cnt[1][1]:我们想要新节点的左端点的 1 行和右端点的 1 行联通
// 如果左节点 le 的左端点的 1 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 1 行联通,那么就联通
// 如果左节点 le 的左端点的 1 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 1 行联通,那么就联通
return res; //输出合并后新节点
}3.整体代码
剩下的操作函数和主函数都很简单,直接在整体代码里看就行。
带注释版本:
#include<bits/stdc++.h>
using namespace std;
#define lc(p) (p << 1)
#define rc(p) (p << 1 | 1) //我自己喜欢用的左右子节点的宏定义
const int N = 1e5 + 10;
//线段树端点
struct node {
int l, r; //左右端点
int cnt[3][3]; // connect[0/1][0/1]:左端点的 0/1 行和右端点的 0/1 行联通就为 1,反之为 0
int ra[3]; //roundabout[0]:从左端点的 0 行绕到区间的中间,再绕回来左端点的 1 行,两点联通为 1,反之为 0
//roundabout[1]:从右端点的 0 行绕到区间的中间,再绕回来右端点的 1 行,两点联通为 1,反之为 0
} tr[N << 2]; //线段树空间开 4 倍
int n, valc[N], valr[2][N];
// valc[x]:第 x 列上下联通
// valr[r][x]:第 r 行的 x - 1 列 和 x 列联通
// 因为给出修改的路径的都是相邻的,所以 valr 就很好用,详见主函数
// 合并函数
node merge(node le, node re) { // 输入左右节点
node res; // 新建合并后节点
res.l = le.l; res.r = re.r; // 新节点左右端点赋值
res.ra[0] = ( le.ra[0] | (le.cnt[0][0] & valr[0][re.l] & re.ra[0] & valr[1][re.l] & le.cnt[1][1]) );
// ra[0]:我们想从新节点的左端点的 0 行绕到区间的中间,再绕回来左端点的 1 行,两点联通
// 如果左节点 le 可以这么做,那就直接可以
// 否则要先从 le 左端点的 0 行到 le 右端点的 0 行,第 0 行再从 le 右端点到 re 左端点
// 判断右节点 re 的 ra[0],再从第 1 行的 re 左端点到 le 右端点,从 le 右端点的 1 行到 le 左端点的 1 行
res.ra[1] = ( re.ra[1] | (re.cnt[0][0] & valr[0][re.l] & le.ra[1] & valr[1][re.l] & re.cnt[1][1]) );
// ra[1]:我们想从新节点的右端点的 0 行绕到区间的中间,再绕回来右端点的 1 行,两点联通
// 如果右节点 re 可以这么做,那就直接可以
// 否则要先从 re 右端点的 0 行到 re 左端点的 0 行,第 0 行再从 re 左端点到 le 右端点
// 判断左节点 le 的 ra[1],再从第 1 行的 le 右端点到 re 左端点,从 le 左端点的 1 行到 le 右端点的 1 行
res.cnt[0][0] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][0]) );
// cnt[0][0]:我们想要新节点的左端点的 0 行和右端点的 0 行联通
// 如果左节点 le 的左端点的 0 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 0 行联通,那么就联通
// 如果左节点 le 的左端点的 0 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 0 行联通,那么就联通
res.cnt[0][1] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][1]) );
// cnt[0][1]:我们想要新节点的左端点的 0 行和右端点的 1 行联通
// 如果左节点 le 的左端点的 0 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 1 行联通,那么就联通
// 如果左节点 le 的左端点的 0 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 1 行联通,那么就联通
res.cnt[1][0] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][0]) );
// cnt[1][0]:我们想要新节点的左端点的 1 行和右端点的 0 行联通
// 如果左节点 le 的左端点的 1 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 0 行联通,那么就联通
// 如果左节点 le 的左端点的 1 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 0 行联通,那么就联通
res.cnt[1][1] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][1]) );
// cnt[1][1]:我们想要新节点的左端点的 1 行和右端点的 1 行联通
// 如果左节点 le 的左端点的 1 行和右端点的 0 行联通,第 0 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 0 行和右端点的 1 行联通,那么就联通
// 如果左节点 le 的左端点的 1 行和右端点的 1 行联通,第 1 行再从 le 右端点到 re 左端点
// 并且右节点 re 的左端点的 1 行和右端点的 1 行联通,那么就联通
return res; //输出合并后新节点
}
void build(int p, int l, int r) { //建树
tr[p].l = l; tr[p].r = r;
tr[p].cnt[0][1] = tr[p].cnt[1][0] = 0; //初始化
tr[p].ra[0] = tr[p].ra[1] = 0;
if (l == r) { // 当只有一列的时候
tr[p].cnt[0][0] = tr[p].cnt[1][1] = 1;
// 左端点的 0 行和右端点的 0 行联通,左端点的 1 行和右端点的 1 行联通
//反正就一列,一行就一个
return;
}
int mid = (l + r) >> 1;
build(lc(p), l, mid);
build(rc(p), mid + 1, r);
tr[p] = merge(tr[lc(p)], tr[rc(p)]); //这个函数下面会讲
}
//这俩操作函数传进去的 x 都是列
void update(int x, int p) { //更新函数
if (x < tr[p].l || tr[p].r < x) { // x 不在当前节点范围内
return ;
}
if (tr[p].l == tr[p].r) { //如果这个节点只有一列
tr[p].ra[0] = tr[p].ra[1] = tr[p].cnt[0][1] = tr[p].cnt[1][0] = valc[tr[p].l];
// ra 和 cnt[1/0][0/1] 都指望着上下连不连通了
return;
}
update(x, lc(p));
update(x, rc(p));
tr[p] = merge(tr[lc(p)], tr[rc(p)]); //改完了别忘了合并
}
node query(int l, int r, int p) { //询问函数
if (l <= tr[p].l && tr[p].r <= r) { //节点区间被包含在询问范围内
return tr[p];
}
int mid = (tr[p].l + tr[p].r) >> 1;
if (r <= mid) {
return query(l, r, lc(p));
}
if (l > mid) {
return query(l, r, rc(p));
}
return merge( query(l, r, lc(p)), query(l, r, rc(p)) ); //合并
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
build(1,1,n);
char s[10]; //开大点,防止奇怪空格
while (cin >> s) {
if (s[0] == 'E') {
break;
}
int ra, ca, rb, cb;
cin >> ra >> ca >> rb >> cb;
-- ra; -- rb;
if (ca > cb) { //保证列从小到大
swap(ra, rb);
swap(ca, cb);
}
if(s[0] == 'O'){ //疏通
if (ca == cb) {
valc[ca] = 1; //单列连通性
}
else { //这里的 ra 和 rb 是一样的
valr[rb][cb] = 1; //相邻列连通性
}
update(cb, 1);
}
else if(s[0] == 'C') { //堵塞
if (ca == cb) {
valc[ca] = 0;
}
else {
valr[rb][cb] = 0;
}
update(cb, 1);
}
else { //询问
node tmpl = query(1, ca, 1);
node tmp = query(ca, cb, 1);
node tmpr = query(cb, n, 1);
if (tmp.cnt[ra][rb]) { //直接连通就再好不过了
cout << "Y" << "\n";
}
else if (tmp.cnt[ra][rb ^ 1] && tmpr.ra[0]) { //先连到右端点不同行,再走到询问区间右边改变行,最后回来
cout << "Y" << "\n";
}
else if (tmp.cnt[ra ^ 1][rb] && tmpl.ra[1]) { //先连到左端点不同行,再走到询问区间左边改变行,最后回来
cout << "Y" << "\n";
}
else if (tmp.cnt[ra ^ 1][rb ^ 1] && tmpl.ra[1] && tmpr.ra[0]) { //两边都连不同行,两边都改完行再回来
cout << "Y" << "\n";
}
else { //实在没招了
cout << "N" << "\n";
}
}
}
return 0;
}
不带注释方便调试的版本:
#include<bits/stdc++.h>
using namespace std;
#define lc(p) p << 1
#define rc(p) p << 1 | 1
const int N = 1e5 + 10;
struct node {
int l, r;
int cnt[3][3];
int ra[3];
} tr[N << 2];
int n, valc[N], valr[3][N];
node merge(node le, node re) {
node res;
res.l = le.l; res.r = re.r;
res.ra[0] = ( le.ra[0] | (le.cnt[0][0] & valr[0][re.l] & re.ra[0] & valr[1][re.l] & le.cnt[1][1]) );
res.ra[1] = ( re.ra[1] | (re.cnt[0][0] & valr[0][re.l] & le.ra[1] & valr[1][re.l] & re.cnt[1][1]) );
res.cnt[0][0] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][0]) );
res.cnt[0][1] = ( (le.cnt[0][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[0][1] & valr[1][re.l] & re.cnt[1][1]) );
res.cnt[1][0] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][0]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][0]) );
res.cnt[1][1] = ( (le.cnt[1][0] & valr[0][re.l] & re.cnt[0][1]) | (le.cnt[1][1] & valr[1][re.l] & re.cnt[1][1]) );
return res;
}
void build(int p, int l, int r) {
tr[p].l = l; tr[p].r = r;
tr[p].ra[0] = tr[p].ra[1] = 0;
tr[p].cnt[0][1] = tr[p].cnt[1][0] = 0;
if (l == r) {
tr[p].cnt[0][0] = tr[p].cnt[1][1] = 1;
return ;
}
int mid = (l + r) >> 1;
build(lc(p), l, mid);
build(rc(p), mid + 1, r);
tr[p] = merge(tr[lc(p)], tr[rc(p)]);
}
void update(int x, int p) {
if (x < tr[p].l || x > tr[p].r) {
return ;
}
if (tr[p].l == tr[p].r) {
tr[p].ra[0] = tr[p].ra[1] = tr[p].cnt[0][1] = tr[p].cnt[1][0] = valc[tr[p].l];
return ;
}
update(x, lc(p));
update(x, rc(p));
tr[p] = merge(tr[lc(p)], tr[rc(p)]);
}
node query(int l, int r, int p) {
if (l <= tr[p].l && tr[p].r <= r) {
return tr[p];
}
int mid = (tr[p].l + tr[p].r) >> 1;
if (r <= mid) {
return query(l, r, lc(p));
}
if(l > mid) {
return query(l, r, rc(p));
}
return merge(query(l, r, lc(p)), query(l, r, rc(p)));
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
build(1, 1, n);
char s[10];
while (cin >> s) {
if (s[0] == 'E') {
break;
}
int ra, ca, rb, cb;
cin >> ra >> ca >> rb >> cb;
-- ra; -- rb;
if (ca > cb) {
swap(ra, rb);
swap(ca, cb);
}
if (s[0] == 'O') {
if (ca == cb) {
valc[ca] = 1;
}
else {
valr[rb][cb] = 1;
}
update(cb, 1);
}
else if (s[0] == 'C'){
if (ca == cb) {
valc[ca] = 0;
}
else {
valr[rb][cb] = 0;
}
update(cb, 1);
}
else {
node tmpl = query(1, ca, 1);
node tmp = query(ca, cb, 1);
node tmpr = query(cb, n, 1);
if (tmp.cnt[ra][rb]) {
cout << "Y" << "\n";
}
else if (tmp.cnt[ra][rb ^ 1] && tmpr.ra[0]) {
cout << "Y" << "\n";
}
else if (tmp.cnt[ra ^ 1][rb] && tmpl.ra[1]) {
cout << "Y" << "\n";
}
else if (tmp.cnt[ra ^ 1][rb ^ 1] && tmpl.ra[1] && tmpr.ra[0]) {
cout << "Y" << "\n";
}
else {
cout << "N" << "\n";
}
}
}
return 0;
}