十三，数据结构-树-EW帮帮网

定义

树也是基于节点的数据结构，和链表不同的是，树的节点可以指向多个节点。首先对树的一些常用术语进行说明：

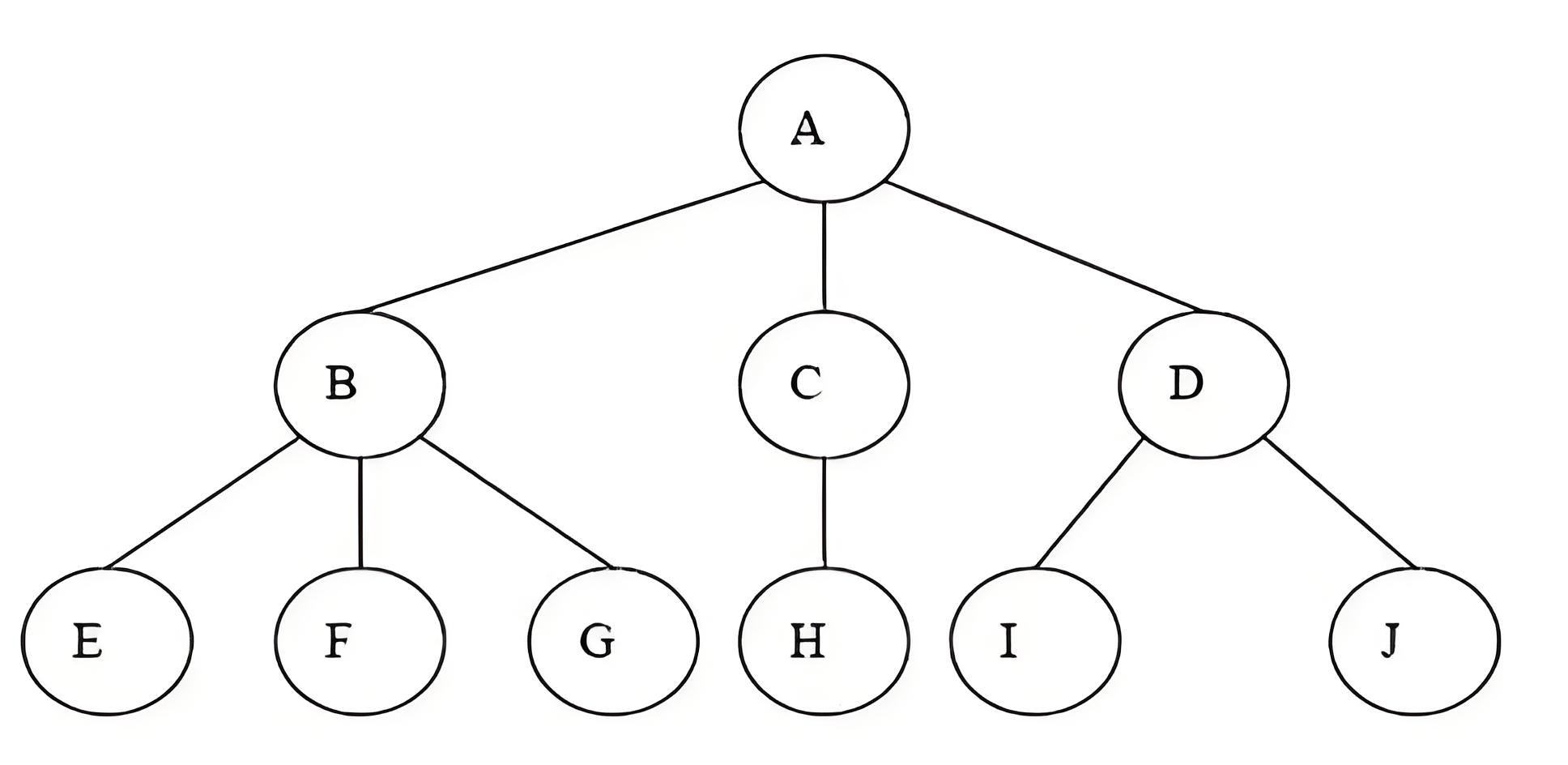
最上面的节点叫做根节点，根位于树顶，如图中的节点A；
和族谱一样，节点有后代和祖先；节点的后代即起源于该节点的全部节点，祖先即可以派生出该节点的节点；
树有层级，每一层都是树的一行，如上图，树有三层；
树的一个属性是它是否平衡，即如果子树中的节点数量相同，则这棵树是平衡的，上图中的树就是不平衡的；

二叉查找树

二叉查找树也是树的一种，其特征如下：

每个节点最多有一个左子节点和右子节点
一个节点的左子树中的值都小于节点本身，同时右子树中的值都大于节点本身；

实现

二叉树实现如下：

#include <iostream>
#include <memory>

// 二叉树节点类
template <typename T>
class TreeNode {
public:
    T data;
    std::shared_ptr<TreeNode<T>> left;
    std::shared_ptr<TreeNode<T>> right;
    
    TreeNode(T value) : data(value), left(nullptr), right(nullptr) {}
};

二叉树查找

二叉树查找步骤如下：

以根节点为当前节点；
读取当前节点数值；
如果当前数值为要查找的数值，则停止查找并返回；
如果当前值大于要查找的数值，则在其左子树中继续查找；
如果当前值小于要查找的数值，则在右子树中继续查找；
重复1-5步，直到找到对应数值，或者到达了树的底端，即数值不在该树中；

注意观察可以发现，每次查找都会排除大约一半的节点，因此可以推测二叉查找树的查找效率为O( $log_{2}N$ )，之所以说大约为这个效率，是因为只有二叉查找树的每一行节点都填满（即是一棵平衡二叉树），则上述特性才成立即：如果一棵平衡的二叉树中有N个节点，则就会有大约logN层。代码实现如下：

bool searchRecursive(std::shared_ptr<TreeNode<T>> node, T value) const {
        if (!node) {
            return false;
        }
        
        if (value == node->data) {
            return true;
        } else if (value < node->data) {
            return searchRecursive(node->left, value);
        } else {
            return searchRecursive(node->right, value);
        }
    }

二叉树插入

二叉树的插入是基于二叉树的查找，即找到要插入的位置后插入（方法同上述中的二叉树查找），其效率为O(logN)+1,代码实现如下：

    // 递归插入节点
    std::shared_ptr<TreeNode<T>> insertRecursive(std::shared_ptr<TreeNode<T>> node, T value) {
        if (!node) {
            return std::make_shared<TreeNode<T>>(value);
        }
        
        if (value < node->data) {
            node->left = insertRecursive(node->left, value);
        } else if (value > node->data) {
            node->right = insertRecursive(node->right, value);
        }
        
        return node;
    }

二叉树删除

二叉树查找树的删除是最复杂的部分，其步骤如下：

如果要删除的节点没有子节点，那么就可以直接删除该节点；
如果要删除的节点有一个子节点，那么就在删除该节点的同时把子节点插到该节点的位置；
如果要删除的节点有两个子节点，则需要把要删除的节点替换为其后继节点，后继节点即大于被删除节点的所有子节点中最小的那个；
如果需要寻找后继节点，则需要先移动到被删除节点的右子节点，然后沿左节点的链接移动到左子结点，直到找不到任何左子结点为止，最下的这个值即后继节点；
如果后继节点有一个右子节点，则在将后继节点放置到被删除节点的位置之后，把这个右子节点变成后继节点曾经的父节点的左子结点。

删除的效率和插入以及查找类似，均为O(logN)，代码如下：

    // 查找最小节点
    std::shared_ptr<TreeNode<T>> findMin(std::shared_ptr<TreeNode<T>> node) const {
        while (node && node->left) {
            node = node->left;
        }
        return node;
    }

    // 递归删除节点
    std::shared_ptr<TreeNode<T>> deleteRecursive(std::shared_ptr<TreeNode<T>> node, T value) {
        if (!node) {
            return nullptr;
        }
        
        if (value < node->data) {
            node->left = deleteRecursive(node->left, value);
        } else if (value > node->data) {
            node->right = deleteRecursive(node->right, value);
        } else {
            // 找到要删除的节点
            if (!node->left) {
                return node->right;
            } else if (!node->right) {
                return node->left;
            }
            
            // 有两个子节点的情况：找到右子树的最小节点替换当前节点
            std::shared_ptr<TreeNode<T>> temp = findMin(node->right);
            node->data = temp->data;
            node->right = deleteRecursive(node->right, temp->data);
        }
        
        return node;
    }

遍历-前、中、后

二叉查询树的遍历，即访问所有节点，分类为三种：前序、中序、后序。其实这里的前、中、后针对的是调用遍历函数时的当前节点，前的意思就是先访问当前节点，再访问左、右子节点；中的意思就是先访问左子节点，再访问当前节点，最后访问右子节点；后的意思是先访问左、右子节点，最后访问本节点，其实现如下：

    // 中序遍历（递归）
    void inorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        inorderRecursive(node->left);
        std::cout << node->data << " ";
        inorderRecursive(node->right);
    }
    
    // 前序遍历（递归）
    void preorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        std::cout << node->data << " ";
        preorderRecursive(node->left);
        preorderRecursive(node->right);
    }
    
    // 后序遍历（递归）
    void postorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        postorderRecursive(node->left);
        postorderRecursive(node->right);
        std::cout << node->data << " ";
    }

以上就是本节关于二叉查找树的全部内容，树还有很多形式，这里挑选比较常用、简单的树形结构来进行讲解，不过今后有了AI，这些数据结构和算法的实现将会比较简单，程序员更多地是理解原理以及优化。全部代码整理如下：

#include <iostream>
#include <memory>

// 二叉树节点类
template <typename T>
class TreeNode {
public:
    T data;
    std::shared_ptr<TreeNode<T>> left;
    std::shared_ptr<TreeNode<T>> right;
    
    TreeNode(T value) : data(value), left(nullptr), right(nullptr) {}
};

// 二叉查找树类
template <typename T>
class BinarySearchTree {
private:
    std::shared_ptr<TreeNode<T>> root;
    
    // 递归插入节点
    std::shared_ptr<TreeNode<T>> insertRecursive(std::shared_ptr<TreeNode<T>> node, T value) {
        if (!node) {
            return std::make_shared<TreeNode<T>>(value);
        }
        
        if (value < node->data) {
            node->left = insertRecursive(node->left, value);
        } else if (value > node->data) {
            node->right = insertRecursive(node->right, value);
        }
        
        return node;
    }
    
    // 递归查找节点
    bool searchRecursive(std::shared_ptr<TreeNode<T>> node, T value) const {
        if (!node) {
            return false;
        }
        
        if (value == node->data) {
            return true;
        } else if (value < node->data) {
            return searchRecursive(node->left, value);
        } else {
            return searchRecursive(node->right, value);
        }
    }
    
    // 查找最小节点
    std::shared_ptr<TreeNode<T>> findMin(std::shared_ptr<TreeNode<T>> node) const {
        while (node && node->left) {
            node = node->left;
        }
        return node;
    }
    
    // 递归删除节点
    std::shared_ptr<TreeNode<T>> deleteRecursive(std::shared_ptr<TreeNode<T>> node, T value) {
        if (!node) {
            return nullptr;
        }
        
        if (value < node->data) {
            node->left = deleteRecursive(node->left, value);
        } else if (value > node->data) {
            node->right = deleteRecursive(node->right, value);
        } else {
            // 找到要删除的节点
            if (!node->left) {
                return node->right;
            } else if (!node->right) {
                return node->left;
            }
            
            // 有两个子节点的情况：找到右子树的最小节点替换当前节点
            std::shared_ptr<TreeNode<T>> temp = findMin(node->right);
            node->data = temp->data;
            node->right = deleteRecursive(node->right, temp->data);
        }
        
        return node;
    }
    
    // 中序遍历（递归）
    void inorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        inorderRecursive(node->left);
        std::cout << node->data << " ";
        inorderRecursive(node->right);
    }
    
    // 前序遍历（递归）
    void preorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        std::cout << node->data << " ";
        preorderRecursive(node->left);
        preorderRecursive(node->right);
    }
    
    // 后序遍历（递归）
    void postorderRecursive(std::shared_ptr<TreeNode<T>> node) const {
        if (!node) return;
        
        postorderRecursive(node->left);
        postorderRecursive(node->right);
        std::cout << node->data << " ";
    }
    
public:
    BinarySearchTree() : root(nullptr) {}
    
    // 插入值
    void insert(T value) {
        root = insertRecursive(root, value);
    }
    
    // 查找值
    bool search(T value) const {
        return searchRecursive(root, value);
    }
    
    // 删除值
    void remove(T value) {
        root = deleteRecursive(root, value);
    }
    
    // 中序遍历
    void inorder() const {
        std::cout << "中序遍历: ";
        inorderRecursive(root);
        std::cout << std::endl;
    }
    
    // 前序遍历
    void preorder() const {
        std::cout << "前序遍历: ";
        preorderRecursive(root);
        std::cout << std::endl;
    }
    
    // 后序遍历
    void postorder() const {
        std::cout << "后序遍历: ";
        postorderRecursive(root);
        std::cout << std::endl;
    }
    
    // 判断树是否为空
    bool isEmpty() const {
        return root == nullptr;
    }
};

// 示例用法
int main() {
    BinarySearchTree<int> bst;
    
    // 插入一些值
    bst.insert(50);
    bst.insert(30);
    bst.insert(20);
    bst.insert(40);
    bst.insert(70);
    bst.insert(60);
    bst.insert(80);
    
    // 遍历二叉树
    bst.inorder();
    bst.preorder();
    bst.postorder();
    
    // 搜索值
    std::cout << "搜索 40: " << (bst.search(40) ? "找到" : "未找到") << std::endl;
    std::cout << "搜索 90: " << (bst.search(90) ? "找到" : "未找到") << std::endl;
    
    // 删除值
    std::cout << "\n删除 20\n";
    bst.remove(20);
    bst.inorder();
    
    std::cout << "删除 30\n";
    bst.remove(30);
    bst.inorder();
    
    std::cout << "删除 50\n";
    bst.remove(50);
    bst.inorder();
    
    return 0;
}

十三，数据结构-树

定义

二叉查找树

实现

二叉树查找

二叉树插入

二叉树删除

遍历-前、中、后

网站公告

今日签到

热门文章

最新发布