https://www.lamda.nju.edu.cn/aml24fall/slides/Chap10.pptx
目录
1.MDS (Multiple Dimensional Scaling) 多维缩放方法
2. 主成分分析 (Principal Component Analysis, PCA)
4.1 LLE 局部线性嵌入(Locally Linear Embedding)
5. 距离度量学习 (distance metric learning)
5.3 LMNN:Large Margin Nearest Neighbors
聚类 近朱者赤近墨者黑 kNN k的选取(参数影响结果 参数敏感性)+ 距离计算
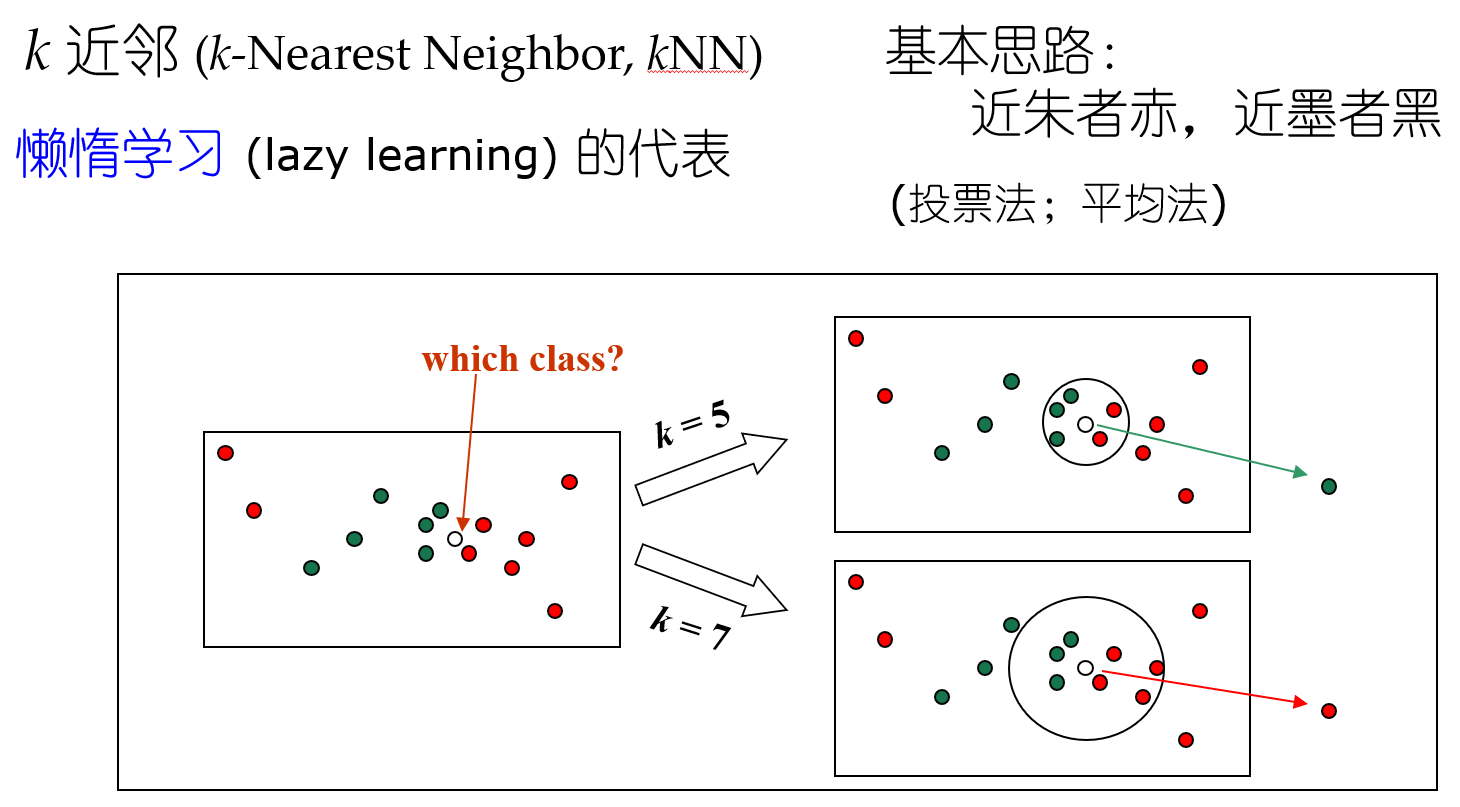
密采样(dense sampling) 高维维度爆炸
如果近邻的距离阈值设为10^-3,
假定维度为20,如果样本需要满足密采样条件,需要的样本数量近10^60。
高维距离计算困难 内积都很困难,所以需要降维。
人是三维生物 但我们说要去某个地理位置 就说二维位置。(数据本身暗含低维假设 数据冗余)
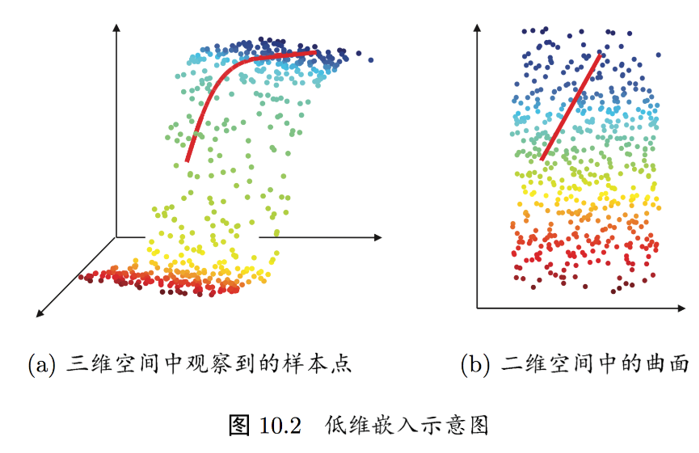
打蚊子降维; 梵高的画流形(非线性) 毕加索的画分段线性
1.MDS (Multiple Dimensional Scaling) 多维缩放方法
旨在寻找一个低维子空间,样本在此子空间内的距离和样本原有距离尽量保持不变。
线性降维:矩阵乘法。
变形问题:如何在低维子空间和高维空间之间保持样本之间的内积不变?后续证明 保内积<=>保距离。
设样本之间的内积矩阵均为B 对B进行特征值分解:![]()
![]()
![]()
谱分布长尾:存在相当数量的小特征值 ; 只保留前几个大维度特征。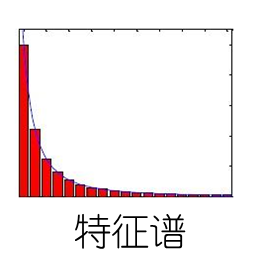
内积可以求取距离 ![]()
距离矩阵D 可以求取内积矩阵B. 所以保内积 等价 保距离不变。
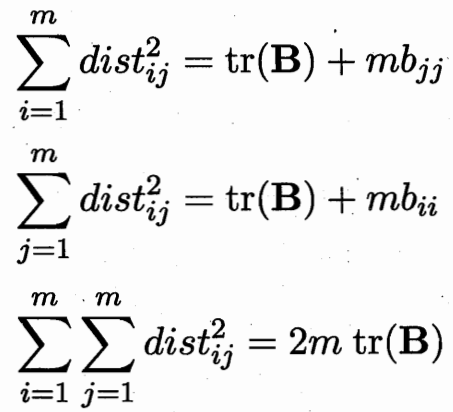
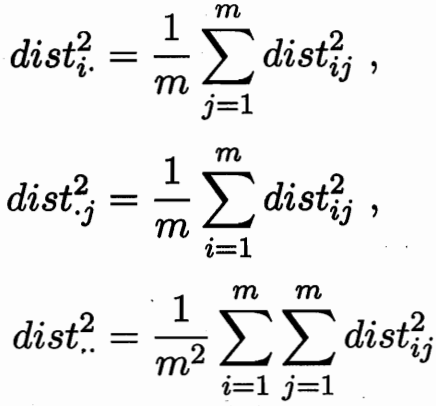
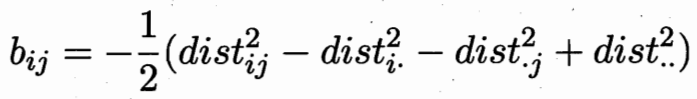
2. 主成分分析 (Principal Component Analysis, PCA)
正交属性空间中的样本点,如何使用一个超平面对所有样本进行恰当的表达?
把散点拍到一个平面 主成分分析的两种等价推导:最近重构性 与 最大可分性
1. 最近重构性:样本点到这个超平面的距离都足够近(平面拟合这些点 都很近)
样本中心化 + 标准正交基 ![]()
3i+4j+5k = (3,4,5)·(i,j,k) 内积 如何得到3? 和i做内积即可。 某方向的投影,即和那个方向的基做内积。
![]()
 w空间下的z 反推x,各个分量加起来。
w空间下的z 反推x,各个分量加起来。

最小化这个迹 并基正交,可以转化为优化问题 是一个QCQP问题
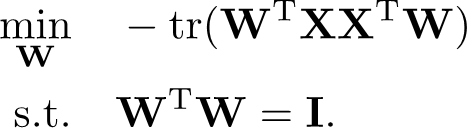
拉格朗日乘子法可得 ![]()
2. 最大可分性:样本点在这个超平面上的投影能尽可能分开
保持样本本身的特性 -- 保留样本和其他样本的差异性 下式和上式相同

2.1 凸优化证明
利用对称矩阵乘上 W^T W 求导 -> 2W

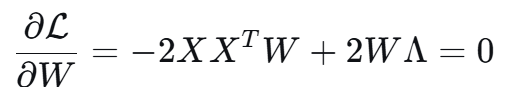
![]()
![]()
2.2 人脸识别降维应用
选取特征基,脸的空间中的基 还是脸; 被称为特征脸eigenface

黑白深浅表示某个局部识别的权重比例 比如第一张图表示头发权重很高,第四张图表示胡子权重很高
3. 核化PCA



4. 流行学习
若低维流形嵌入到高维空间中,则数据样本在高维空间的分布虽然看上去非常复杂, 但在局部上仍具有欧氏空间的性质,因此,可以容易地在局部建立降维映射关系,然后再设法将局部映射关系推广到全局。
可以类比成:世界地图与地球仪 想象一下我们的地球。
高维空间(真实世界):地球本身是一个三维的球体(一个嵌入在三维空间中的二维流形)。你站在上面能感觉到它的弧度,这是一个复杂的曲面。
低维流形:但我们平时使用的世界地图,是一张二维的纸。这张纸就是一个二维的表示。
局部具有欧氏空间性质:虽然整个地球是弯曲的,但你在你家小区、甚至整个城市范围里活动时,你完全可以把地面当成是平的。在这个“局部”范围内,东西南北、距离长短的规则(即欧几里得几何法则)都是成立的。这就叫“局部上仍具有欧氏空间的性质”。
在局部建立降维映射:制图师如何绘制地图呢?他们不会一下子画整个地球。而是会一小块一小块地(比如先画一个城市,再画一个省)进行测绘。在每一小块区域内,因为他们可以把地面当成平的,所以可以非常准确地将三维地形映射到二维纸上。这个过程就是“在局部建立降维映射关系”。
将局部关系推广到全局:最后,制图师需要把所有这些小块的、平整的地图,用某种方法(比如各种地图投影算法)拼接、缝合起来,形成一张完整的、但必然有某种失真(比如格陵兰岛看起来和非洲一样大)的世界地图。这就是“设法将局部映射关系推广到全局”。
4.1 LLE 局部线性嵌入(Locally Linear Embedding)
低维空间 保留近邻关系 + 近邻权重 ;
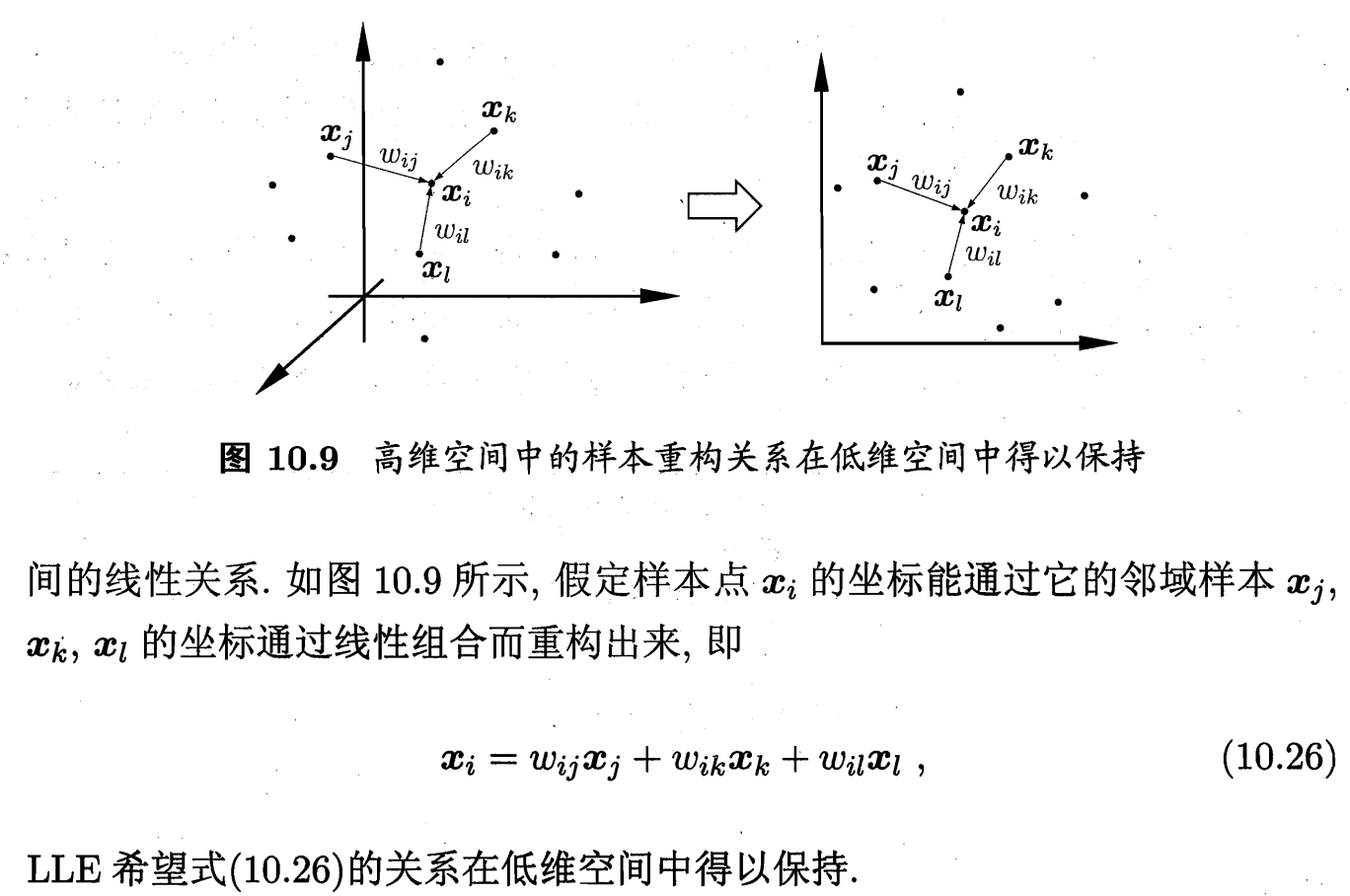
每个数据点都可以由其最近邻的若干个点的线性组合来重构;
第一步:使用 K-NN(K近邻)或 ε-球 的方法找到它的 k 个最近邻点
第二步:计算局部线性关系的权重矩阵 我们试图用它的 k 个近邻点 x_j 来最佳地重构它自己。即,找到一组权重系数 W_ij,使得重构误差最小化
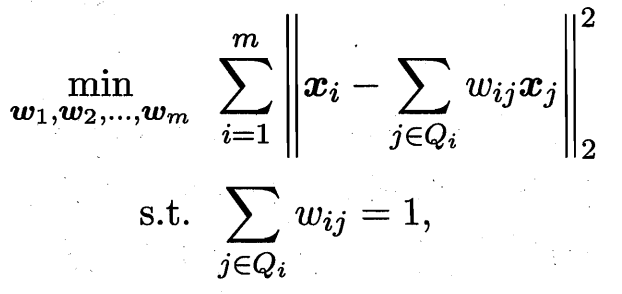
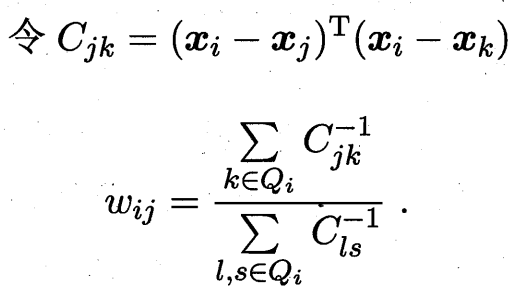
第三步:寻找一组低维表示 y_i 使得第二步中计算出的权重 W_ij 仍然能最好地重构 y_i
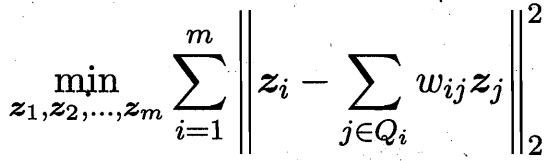
4.2 Isomap(等距特征映射)
测地距离才真实:数据点之间的真实相似性应该用流形上两点之间的最短路径(测地距离)来度量。
瑞士卷展平:理想情况沿着曲面走一圈;保距保的是 展开后平面的距离
飞机两城市飞行轨迹:不只是直接走圆弧 而是要求走的路径经过有机场的城市(失事着陆)
选取一些点 把这些点两两连起来 形成路线 (有点像无向图单源最短路)
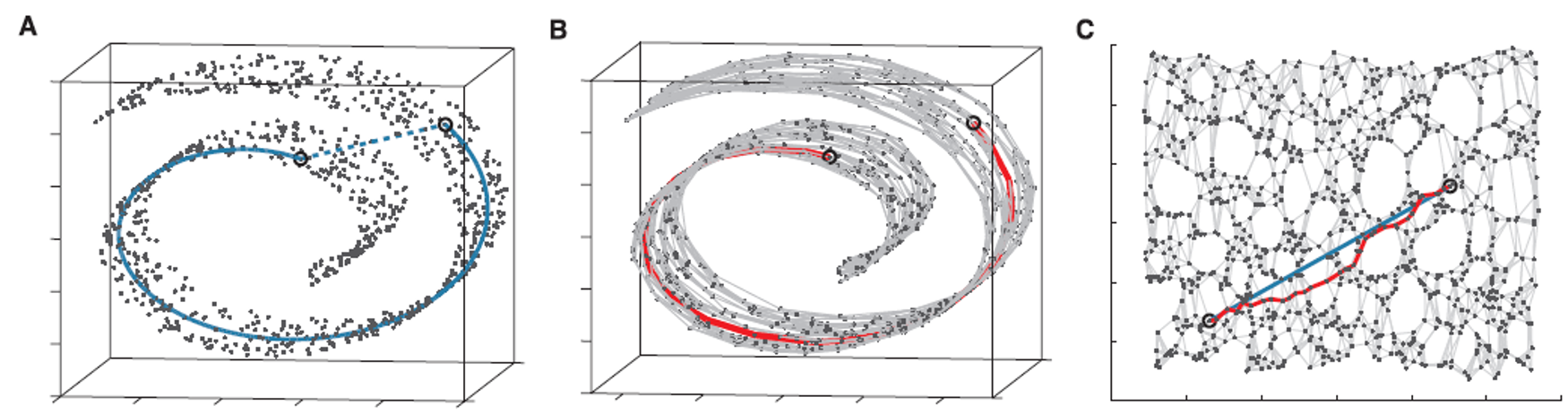
第一步:使用 K-NN(K近邻)或 ε-球 的方法找到它的 k 个最近邻点
第二步:基于最短路径算法 近似任意两点之间的测地线(geodesic)距离
第三步:寻找一个低维表示,使得在低维空间中点与点之间的欧氏距离,尽可能地接近第一步中计算出的测地距离矩阵 D_G
5. 距离度量学习 (distance metric learning)
降维的主要目的是希望找到一个“合适的”低维空间,在那个空间再算欧氏距离。
能否根据data的类别 直接“学出”合适的距离?
核心思想: 让机器从数据中自动学习一个最优的距离度量函数,而不是手动选择。
5.1 马氏距离 度量矩阵M
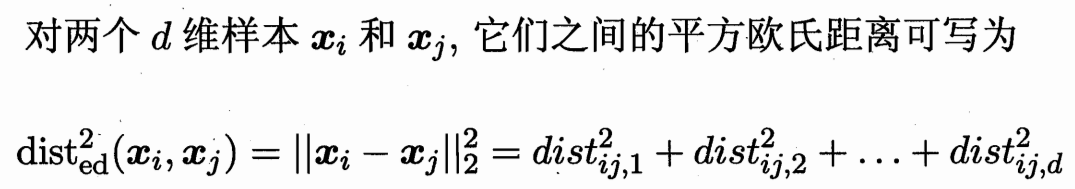
即两个点之间 向量的长度的平方。(xi-xj)^T (xi-xj)
中间乘以一个对角阵 W 即进行不同维度的加权。
中间乘一个半正定对称矩阵(为了保持距离非负且对称)M(度量矩阵)
得到马氏距离 (Mahalanobis distance)
![]()
若已知“必连”(must-link) 约束集合M 目标函数最小化他们之间的距离,
与“勿连”(cannot-link) 约束集合C(最少也要距离1)因为没有对M的尺度放缩限制条件 设置一个常数。
则可转化为求解这个凸优化问题:
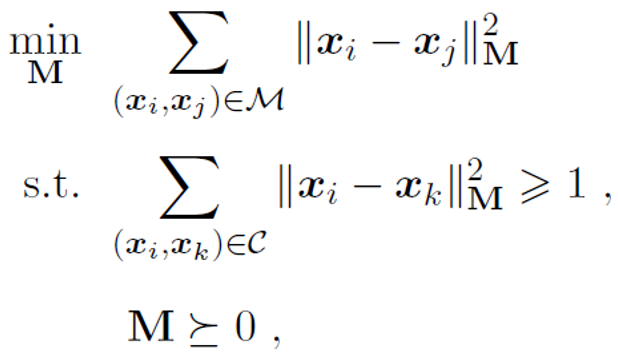
5.2 近邻成分分析 NCA
近邻成分分析(Neighbourhood Component Analysis,简称 NCA) (致敬PCA)
近邻分类器在进行判别时通常使用多数投票法,邻域中的每个样本投1票, 邻域外的样本投0票。
不妨将其替换为概率投票法 j 对 i 投票的影响力,像softmax。
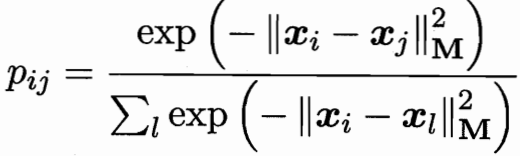
单个样本即 各种j对i的投票和;整个训练集 即所有样本求和。

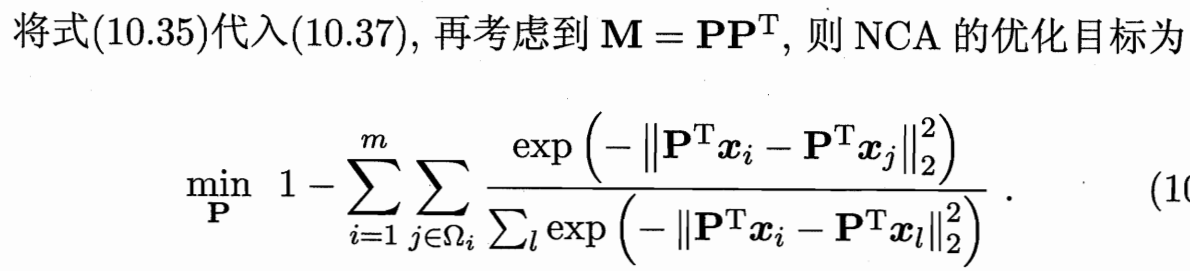
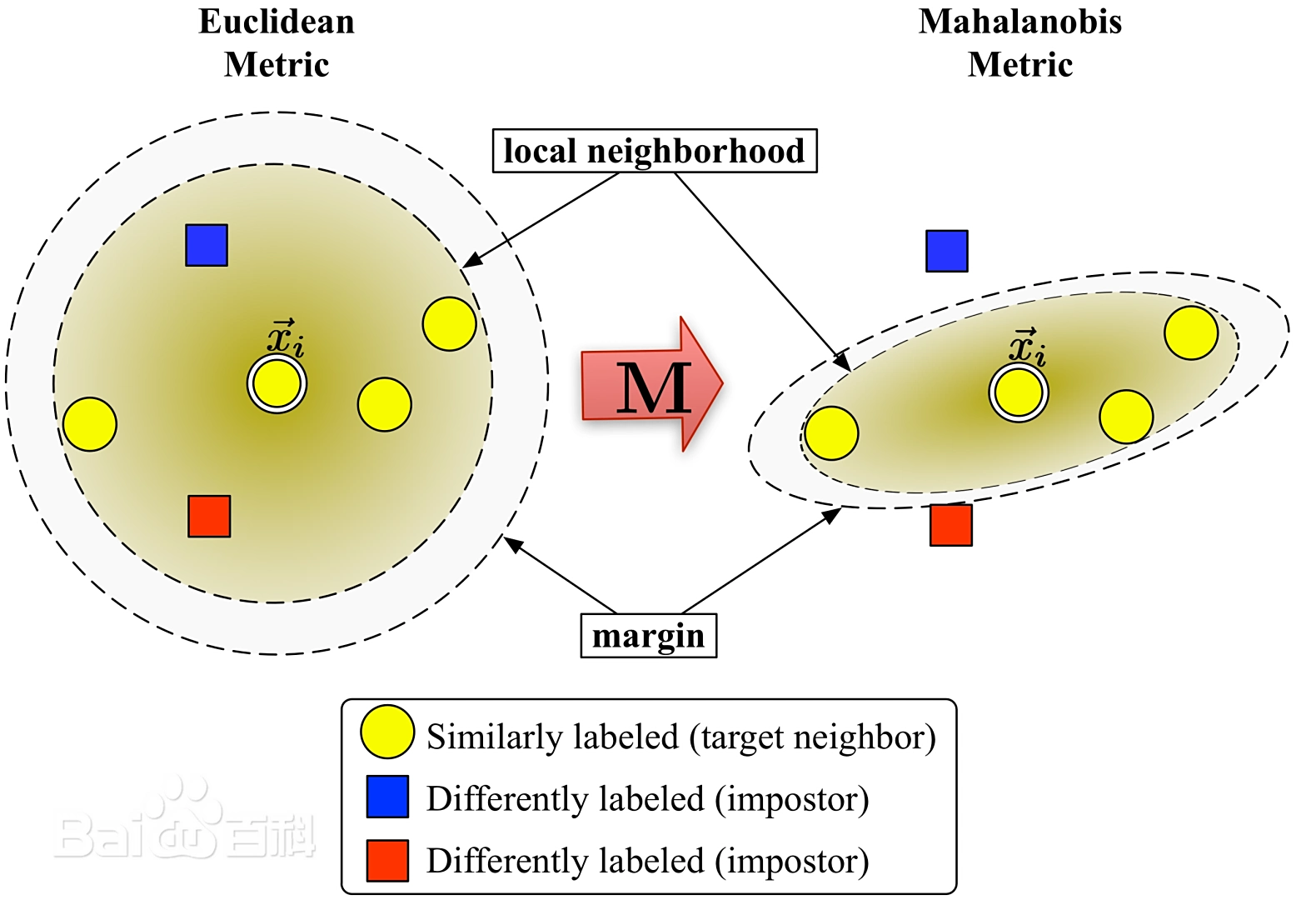
5.3 LMNN:Large Margin Nearest Neighbors
学习一个新的距离度量,使得在这个新的空间里,K-NN算法的性能达到最优。
临近位置 相似标签要尽量近 不同标签尽量远;至少要间隔margin 否则惩罚。
![]() 拉近损失
拉近损失
拉远损失 差值是否>1 的一个0-1变量;写在优化问题中 设置为ε
![]()
![]() 加权一下
加权一下
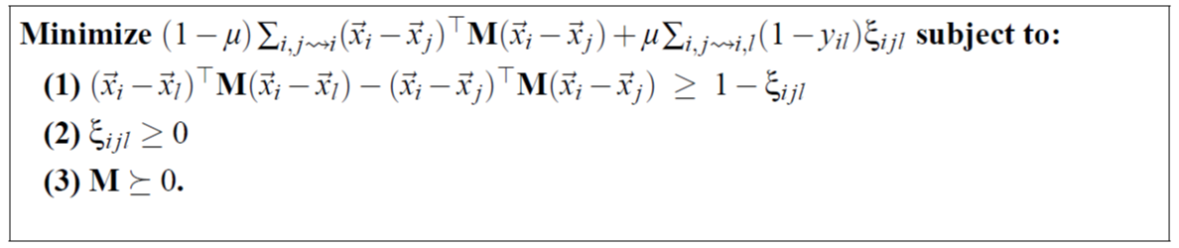
维度降下去了 丢掉了什么信息?丢掉了训练的时候用的信息。
比如上面的 i,j,l 三元组训练。抽取所有三元组 就是n^3级别 不算这么多,进行采样,那么没被采样到的数据 相当于被丢掉了。