目录
参数的打包
1.打包为元组
函数不知道用户需要传入多少个参数,比如print()函数可以支持参数可多可少的情况,拥有这种特性的形参称为收集参数。它的本质是元组,使用元组打包和解包的特性。
>>> def myfunc(*args):
print(type(args))
>>> myfunc()
<class 'tuple'>

如果在收集参数之后还需要指定其他参数,那么在调用函数是,就应该使用关键字参数来指定后面的参数,否则Python就会把实参纳入到收集参数中

2.打包为字典
除了上面的将实参打包为元组,还可以将实参打包为字典
*+形式参数将多个参数打包为元组,**+形式参数将多个参数打包成字典
注意:小甲鱼在字典构造那一节里留了一个悬念,使用dict构造字典时键不需要使用引号,在函数的时候会讲到。
3.还可以将其混合起来,既包含元组也包含字典
如字符串的format方法


参数的解包
在形参上使用称为参数的打包,在实参上使用称为解包
args=(1,2,3,4)
>>> def myfunc(a,b,c,d):
print(a,b,c,d)
>>> myfunc(args)
Traceback (most recent call last):
File "<pyshell#125>", line 1, in <module>
myfunc(args)
TypeError: myfunc() missing 3 required positional arguments: 'b', 'c', and 'd'
>>> myfunc(*args) //解包为元组,一个*
1 2 3 4
>>> kwargs={'a':1,'b':2,'c':3,'d':4}
>>> myfunc(kwargs)
Traceback (most recent call last):
File "<pyshell#128>", line 1, in <module>
myfunc(kwargs)
TypeError: myfunc() missing 3 required positional arguments: 'b', 'c', and 'd'
>>> myfunc(**kwargs) //解包为字典,加两个*
1 2 3 4作用域
作用域是指一个函数可以被访问的范围,由代码中被赋值的位置来决定的
局部作用域
若一个变量被赋值在函数的内部,作用域仅限于该函数中,称为局部变量
全局作用域
若在函数中存在一个跟全局一模一样的局部变量,该全局变量在函数内部可以访问但是不可以修改它的值。
若要在函数内部修改全局变量的值,需要使用global进行声明
嵌套函数
在内部函数中修改外部函数的变量时需要使用nonlocal进行声明
>>> def A():
x=520
def funB():
nonlocal x
x = 880
print("in funB,x={}".format(x))
funB()
print("in funA,x=",x)
>>> A()
in funB,x=880
in funA,x= 880
LEGB规则
英文名称 |
作用域范围 |
注释/说明 |
|
|---|---|---|---|
L |
Local |
局部作用域 |
———— |
E |
Enclosed |
嵌套函数的外层函数作用域 |
在嵌套函数中,局部作用域会覆盖外层函数的作用域,需要使用nonlocal进行声明 |
G |
Global |
全局作用域 |
当局部作用域与全局作用域发生冲突时,Python会使用局部作用域的变量,除非使用Global进行声明 |
B |
Build In |
内置作用域 |
避免使用Python的BIF内置函数作为变量名 |
eg:

闭包
函数只有在定义和调用时采用到小括号
闭包 也称为工厂函数,根据上述现象利用嵌套函数来实现类似工厂的功能。
>>> def power(exp):
def exp_of(base):
return base ** exp
return exp_of
>>> square = power(2) //嵌套函数的外部作用域会被保存下来,在执行该语句时,square指向exp_of这个内部函数,这个函数就记住了外层函数作用域的参数exp=2
>>> cube = power(3) //cube变量指向exp_of这个函数,这个内部函数记住了exp=3
>>> square(2)
4
>>> square(5)
25
>>> cube(2)
8
>>> cube(5)
125
外部函数power相当于一个工厂,由于参数不同,得到了两条不同的生产线
- square 返回参数的平方
- cube 返回参数的立方
用法
使用nonlocal语句可以让嵌套函数的内层函数修改外层函数的变量
>>> def outer():
x = 0
y = 0
def inner(x1,y1):
nonlocal x,y
x += x1
y += y1
print(f"现在,x = {x}, y = {y}")
return inner
>>> move = outer()
>>> move(1,2)
现在,x = 1, y = 2
>>> move(-2,2)
现在,x = -1, y = 4
利用内层函数能够记住外层函数作用域这一特性,且使用nonlocal语句,让内层函数修改外层函数作用域中的变量,实现了带记忆功能的函数。可以应用到游戏开发中记录玩家的位置,保护位置信息。
闭包的两个特性
- 利用嵌套函数的外层作用域具有记忆功能的特性,让数据保存在外层函数的参数或者变量中
- 将内层函数作为返回值返回,从外部函数间接调用内层函数
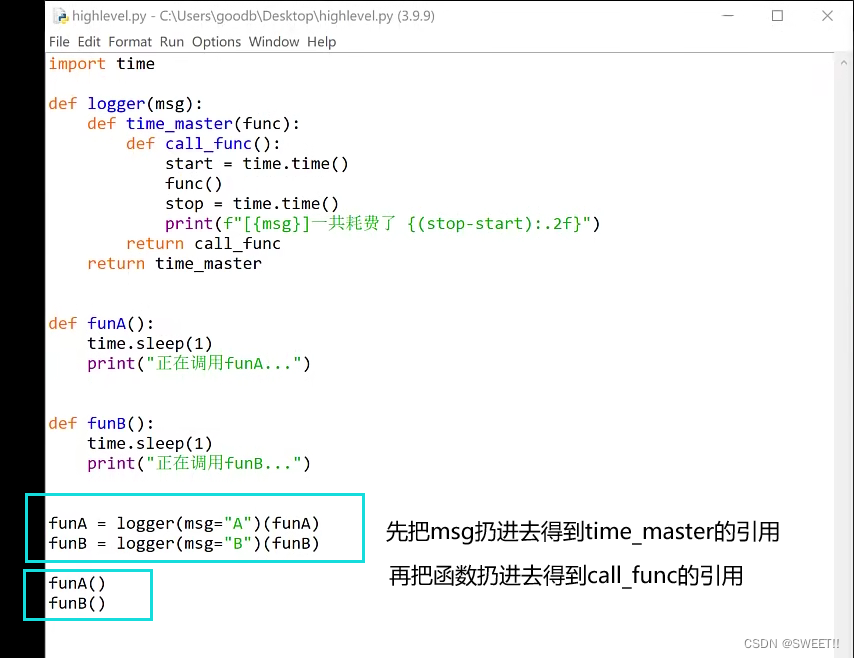
装饰器
既然函数可以作为返回值返回,那么是否可以把函数作为参数传递给另一个函数
>>> import time
>>> def time_master(func):
print("开始运行程序")
start=time.time()
func()
stop=time.time()
print("程序结束运行")
print(f"一共耗费了{(stop-start):.2f}秒。")
>>>
>>> def myfunc():
time.sleep(2)
print("Hello World")
>>> time_master(myfunc) //将函数作为参数传递给另一个函数
开始运行程序
Hello World
程序结束运行
一共耗费了2.04秒。
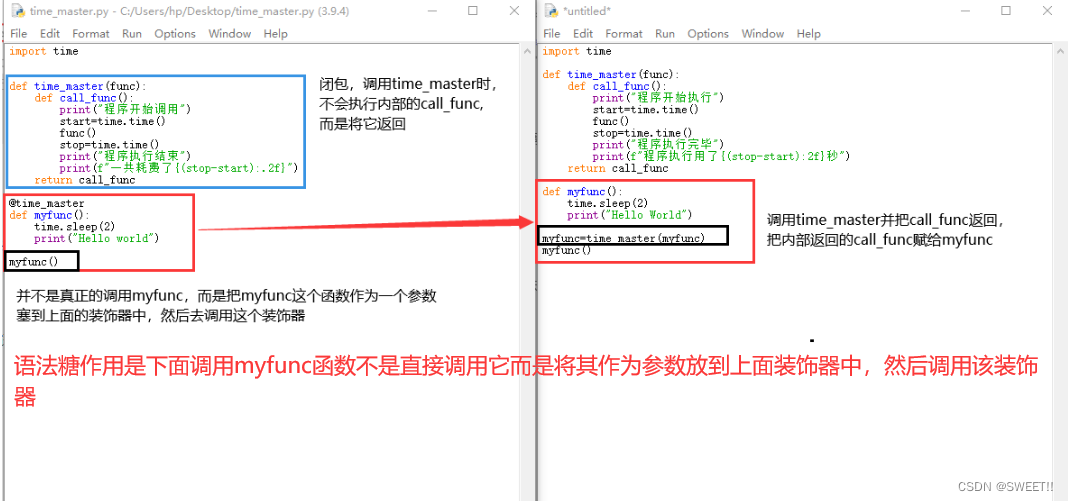
可是如果每次求一个函数的运行时长都要显示的调用time_master函数显然不是最优的解决方案。
改进方案:通过使用装饰器,实现调用my_func()函数时,能够自觉的执行time_master()函数
本质就是闭包,拿函数当参数。
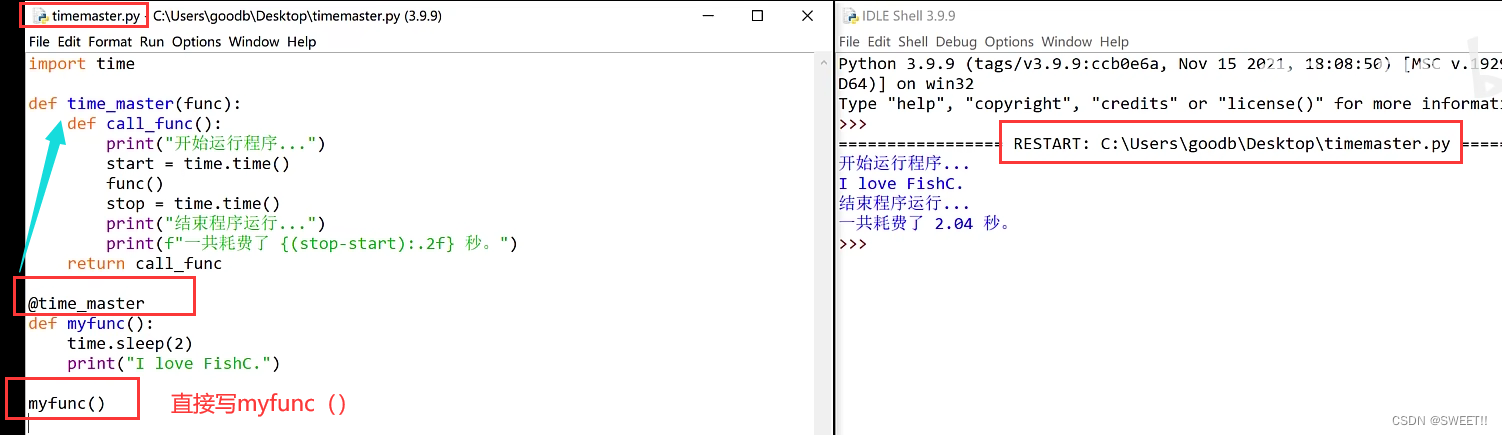
在代码没有显示的调用time_master()函数,但是运用结果与调用的相同
装饰器在实际开发场景中的应用
- 插入日志、添加性能测试或要求先进行权限验证是,就可以通过装饰器在不修改原代码的情况下实现这些功能。
装饰器的原理和本质
- 装饰器的本质是闭包,将函数作为一个参数,类似于语法糖(fstring中提过,语法糖为某种特殊的语法,对函数的功能本身无影响,但是更加简洁)
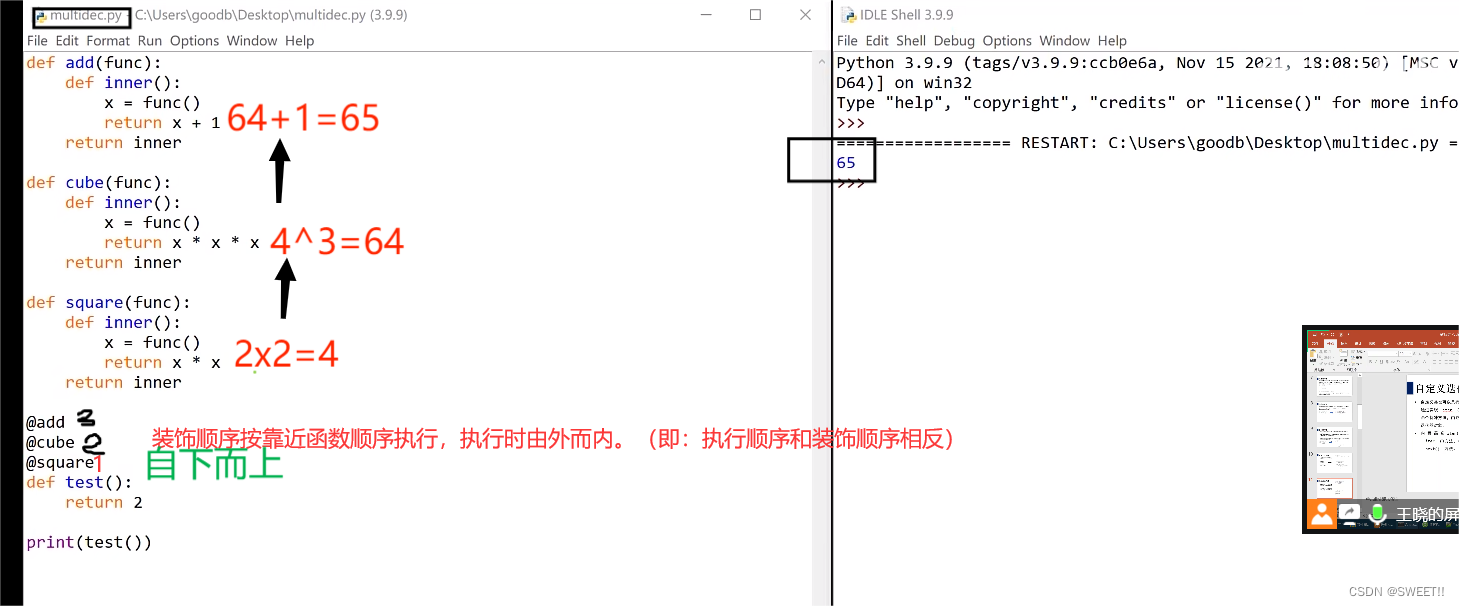
多个装饰器可以用在同一个函数上
代码如下:
//加1
def add(func):
def inner():
x=func() //令x=64,返回64+1
return x+1
return inner
//立方
def cube(func):
def inner():
x=func() //令x=4,返回4的立方
return x*x*x
return inner
//平方
def square(func):
def inner():
x=func()
return x*x
return inner
@add
@cube
@square
def test():
return 2 //装饰器由内向外执行,将test作为参数塞到square这个装饰器中运行,令x=2,返回2的平方
print(test())
代码执行结果如下:
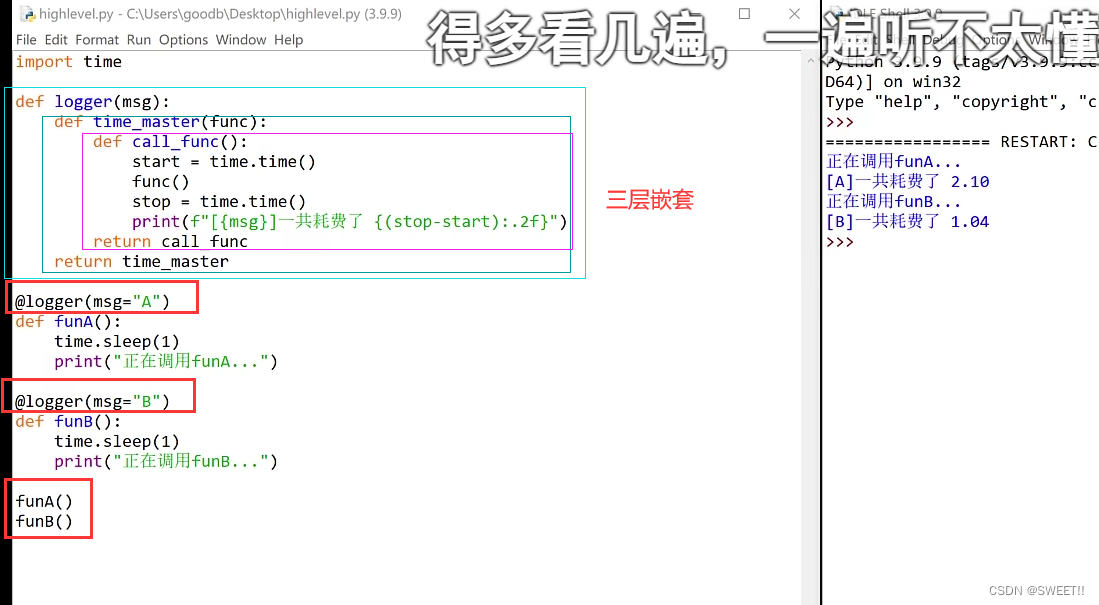
给装饰器传递参数
多加一层函数嵌套,添加一次调用,通过这次调用将参数传递进去
lambda表达式
语法:
- lambda x : 2 * x + 1
- lambda x, y : 2 * x + y
- 调用
- g = lambda x : 2 * x + 1
特点:
- 将函数形式转化为表达式, 省下了定义函数的过程,使代码更加简洁
- 不需要考虑命名的问题
- 增加了可读性,不用跑去看函数使怎么定义的
- 不占用内存资源
- 注:如果使用函数,则可能(猜想)会一直占用内存资源

BIF
filter过滤器
- 语法:filter[function or none, iterable]
- 将iterable(可迭代对象,如列表),中的元素带入function中计算,并返回值为真的元素。
- 如果function为none,则返回iterable中的值为真的元素
- 如:l筛选出值为真的元素
- list(filter(lambda x : x % 2, range(10)))
- 语法:filter[function or none, iterable]
map
- 语法:
- 将序列每个元素作为函数的参数进行加工,直到序列的每个元素都加工完毕,返回新序列
- 如:list(map(lambda x : x % 2, range(10)))
- map里面左边是表达式,右边是参数,最后用list列表展示出来
- 语法:
list(filter(lambda x : x % 2, range(10)))
[1, 3, 5, 7, 9]#输出内容
list(map(lambda x : x % 2, range(10)))
[0, 1, 0, 1, 0, 1, 0, 1, 0, 1]#输出内容
mapped = map(lambda x:ord(x)+10,"wpflovelmy")
list(mapped)
[129, 122, 112, 118, 121, 128, 111, 118, 119, 131]#输出内容生成器
生成器 是迭代的一种方法,在普通的函数里加一个 yield 语句(相当于return)就可以实现生成器
模仿协同程序 ( 协同程序: 可以运行的独立函数调用,函数可以暂停或挂起,并在需要的时候从程序离开的地方继续或者重新开始 )
↓
生成器是一个特殊的函数,调用可以中断或者暂停,并且通过yield返回固定的值。
每调用一个提供一个数据并记住当时的状态
注意:
- 不走回头路
- 支持next()函数,没有了就抛出异常
- 生成器对象无法使用下标索引
生成器实现斐波那契数列
def fib():
n1,n2=0,1
while True:
yield n1
n1,n2 = n2,n1+n2
f=fib()
next(f)
0#输出
next(f)
1#输出生成器推导式
列表推导式会一下子把所有的数据生产出来,生成器表达式一次就生产一个数据
- 用yield替换return
- 直接使用生成器推导式

递归
求阶乘
写一个求阶乘的函数
–正整数阶乘指从1乘以2乘以3乘以4一直乘到所要求的数。
–例如所给的数是5,则阶乘式是1×2×3×4×5,得到的积是120,所以120就是4的阶乘。
#迭代方法
def factorial(n):
result = n
for i in range(1, n):
result *= i
return result
number = int(input('请输入一个正整数:'))
result = factorial(number)
print("%d 的阶乘是:%d"% (number, result))#格式化为整数类型
----
请输入一个正整数:5
5 的阶乘是:120递归方法求大的数阶乘就会比较慢~
#递归方法
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
number = int(input('请输入一个正整数:'))
result = factorial(number)
print("%d 的阶乘是:%d" % (number, result))递归求兔子繁殖:斐波那契数列
函数方法(迭代)

def fab(n):
n1 = 1
n2 = 1
n3 = 1
if n < 1:
print('输入有误!')
return -1
while (n - 2) > 0:
n3 = n2 + n1
n1 = n2
n2 = n3
n -= 1
return n3
result = fab(20)
if result != -1:
print('总共有%d对小兔崽子诞生!' % result)
---
总共有6765对小兔崽子诞生!递归(斐波那契数列)注:迭代计算时间远比递归少,因为递归要循环出入栈
def fab(n):
if n < 1:
print('输入有误!')
return -1
if n == 1 or n == 2:
return 1
else:
return fab(n-1) + fab(n-2)
result = fab(35)
if result != -1:
print('总共有%d对小兔崽子诞生!' % result)
---
总共有9227465对小兔崽子诞生!递归:汉诺塔

def hanoi(n, x, y, z):
if n == 1:
print(x, '-->', z)
else:
hanoi(n-1, x, z, y) # 将n-1个盘子从x移动到y上
print(x, '-->', z) # 将最底下的最后一个盘子从x移动到z上
hanoi(n-1, y, x, z) # 将y上的n-1个盘子移动到z上
n = int(input("请输入汉诺塔层数:"))
hanoi(n, 'X', 'Y', 'Z')类型注释:

内省

高阶函数reduce,partial,@wrap装饰器
reduce:reduce的作用就是将可迭代对象中的元素依次传递到第一个参数指定的函数中
pow(base底数,exp指数)

@wrap装饰器加上去后副作用没有了
