前言

1、本人能力有限，还请大佬多多包涵
2、由于基本没有只含前缀和或差分知识点的题目，就只能用acwing的题目了。但原题要付费才能使用（如有侵权请告知）

介绍前缀和

作用：有一个数组a[N], 构造一个数组S[N] 使得S[N] = a[1] + a[2] + a[3] +…… +a[N]

好处：降低时间复杂度

为了表示方便，将数组下标从l~r之间的数组元素 记为 [l,r] .
例：计算 a[2,5] a[1,6] a[3,4] a[1,5] ……
不难发现：如果用朴素方法求解，每一次计算时都要将[l,r] 之间的元素遍历一遍，for(int i = 2;i<=5;i++) for(int i = 1;i<=6;i++) for(int i = 3;i<=4;i++) …… 这样就会很复杂。

前缀和就是用来改善这种情况的。

一维前缀和

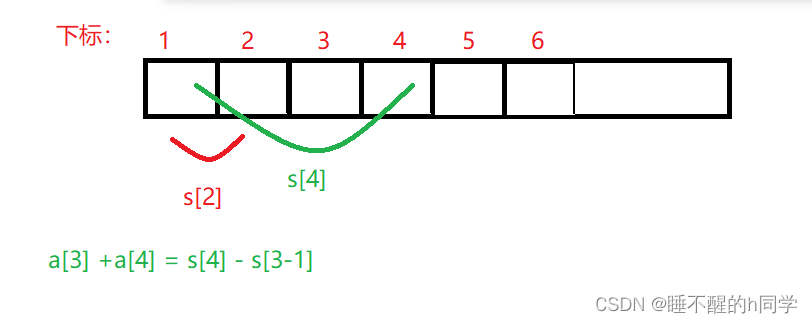
可以由定义得到下列两个公式：

s[N] = s[N-1] + a[N];
a[l] + a[l+1] + ……a[r] = s[r] -s[l-1]

• 因为有[l-1] 所以我们使用数组下标是从1开始使用，避免越界。
• 不用担心a[0]的值会影响结果，因为我们定义a[N]为全局变量，所以a[0]默认就是0。
  s[0] = a[0] = 0; s[1] = s[0]+a[1] =a[1]

例题

输入一个长度为n的数列
接着输入m个询问，每个询问输入l,r ,要求输出数组下标从l~r的元素之和
m<100000

输入描述：第一行输入两个整数n，m
第二行 输入n个数字，代表数组的元素
接下来m行，每行输入两个元素，分别代表l和r

输出描述：输出m行，输出每一个询问的结果

#include<iostream>
using namespace std;

const int N = 100010; //数组卡大一点，防止RE
int a[N];   //全局变量默认初始化为0
int s[N];

int main(){
  int n;m;
  cin>>n>>m;
  for(int i = 1;i<=n;i++) {
     cin>>a[i];
     s[i] = s[i-1] +a[i];  //s[0] 初始化为0 
 }
  
  while(m--){
       int l,r;
       cin>>l>>r;
       cout<<s[r]-s[l-1]<<endl;
  }     
return 0;
}

二维前缀和

先来了解一下s[i,j]的定义：a数组从a[1][1]到a[i][j] 所有元素的和 。
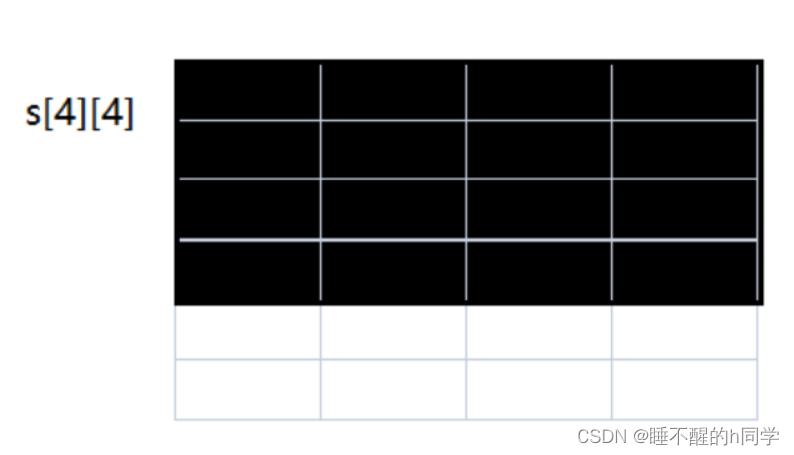
注意： 下标依然从1开始 — (下图表格表示a[ ][ ])

s[N][N]与a[N][N]的关系

举一个例子： s[4][4] = s[3][4]+s[4][3] -s[3][3] +a[4][4]

子矩阵的和

已知一个矩阵的左上角坐标为x1,y1,右下角坐标为x2,y2。如何求这个矩阵之间所有元素的和呢？
(注：左上角坐标为x1,y1,右下角坐标为x2,y2可以表示成 x2>x1,y2>y1)

稍加分析，可以转化为：

公式总结

1、s[n][m] = s[n-1][m]+s[n][m-1]-s[n-1][m-1]+a[n][m]
2、左上角坐标为(x1,y1),右下角坐标为(x2,y2)的矩阵之间元素的和为
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]

一维差分

• 差分本质：已知一个数组a[N]
  构造一个数组b[N] ,使得a[N] =b[1]+b[2]+……+b[N]
  也就是说：差分是前缀和的逆过程
• 用处： 给a[N] 数组 下表从l~r 的元素都加上一个c
  如果用暴力的做法，时间复杂度为O(n) for(int i = l;i<r;i++) a[i] +=c;
  但如果用差分的做法，只需要让b[l]+=c b[r+1] -=c 就可以了
  

例题

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入描述：第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

#include<iostream>
using namespace std;
cosnt int N = 100010;
int a[N];
int b[N];

void Insert(int l,int r,int c){
     b[l] +=c;
     b[r+1] -=c;
}

int main(){
   int n,m;
   cin>>n>>m;
   for(int i = 1;i<=n;i++) {
     scanf("%d",&a[i]);
     Insert(i,i,b[i]);   
  }
  while(m--){
     int l,r;
     cin>>l>>r;
     Insert(l,r,c);
  }
  
  for(int i = 1;i<=n;i++)  b[i] +=b[i-1];
 return 0;
}

二维差分

与一维差分类似，二维差分就是在矩阵中实现差分过程。

类似的，要将数组a[N][N]中从坐标为[x1][y1] 到[x2][y2] 的元素依次加上c
也可以只改变b[N][N]中的元素来实现这一过程。

可以分解为：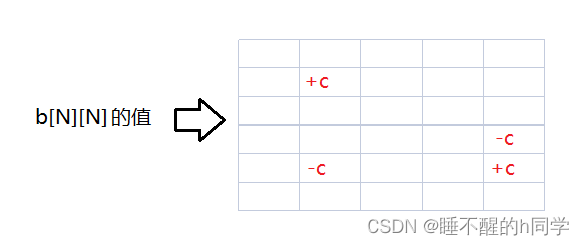
表示为b[x1][y1] += c; b[x2+1][y1] -=c; b[x1][y2+1]-=c; b[x2+1][y2+1] +=c;

例题

其实就是把上面一维差分的模板改一改，就不放原题了，直接上代码

#include<iostream>
using namespace std;

const int N = 1010;
int a[N][N];
int b[N][N];

void Insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x1][y2+1]-=c;
    b[x2+1][y1]-=c;
    b[x2+1][y2+1]+=c;
}

int main(){
   int n,m,q;
   cin>>n>>m>>q;
   
   for(int i = 1;i<=n;i++)
     for(int j = 1;j<=m;j++) 
     {
        cin>>a[i][j];
        Insert(i,j,i,j,a[i][j]);
     }
    
    while(q--){
        int x1,y1,x2,y2,c;
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        Insert(x1,y1,x2,y2,c);
    }
    
    for(int i = 1;i<=n;i++){
      for(int j =1;j<=m;j++) 
      
      {
          b[i][j] += b[i-1][j] + b[i][j-1] -b[i-1][j-1];  //因为之前有为b[i][j]赋值，所以这里要+=
          cout<<b[i][j]<<" ";
      }
     cout<<endl;
  }

}

结束！