1.决策树简介
决策树是一棵树,其中每个分支节点代表多个备选方案之间的选择,每个叶节点代表一个决策。它是一种监督学习算法,主要用于分类问题,适用于分类和连续输入和输出变量。 是归纳推理的最广泛使用和实用的方法之一(归纳推理是从具体例子中得出一般结论的过程)。决策树从给定的例子中学习和训练数据,并预测不可见的情况。
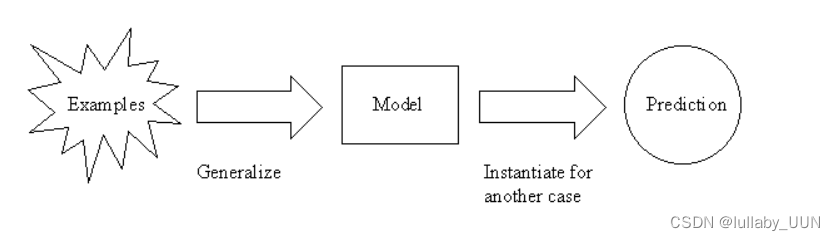
·与决策树相关的重要术语
基本术语:
- 根节点(Root Node):它代表整个种群或样本,并进一步分为两个或更多个同类集。
- 拆分(Splitting):这是将节点划分为两个或更多个子节点的过程。
- 决策节点(Decision Node):当子节点分裂成更多的子节点时,它被称为决策节点。
- 叶子/终端节点(Leaf/ Terminal Node):不分割的节点称为叶子或终端节点。
1.1决策树实例
决策树算法的本质是一种图结构,只需要问一系列问题就可以对数据进行分类
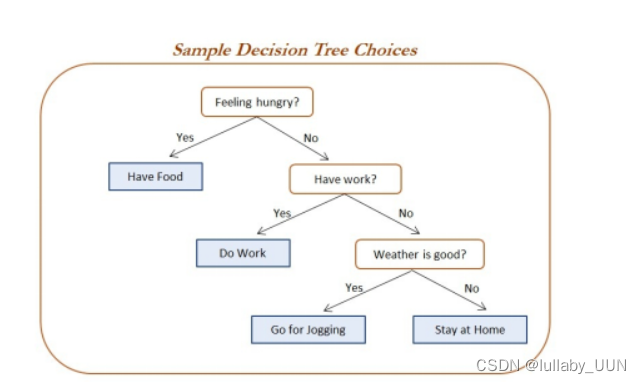
可以看出,在这个决策过程中,我们一直在对记录的特征进行提问。最初的问题所在的地方叫做根节点,在得到结论前的每一个问题都是中间节点,而得到的每一个结论都叫做叶子节点。
决策树算法的核心是要解决两个问题:
(1)如何从数据表中找出最佳节点和最佳分枝?(即怎么构造决策树)
(2)如何让决策树停止生长,防止过拟合?(即如何剪枝)
几乎所有决策树有关的模型调整方法,都围绕这两个问题展开。
1.2基本流程
(1)收集数据
(2)准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
(3)分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
(4)训练算法:构造树的数据结构。
(5)测试算法:使用经验树计算错误率。
(6)使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
2.划分选择
2.1信息增益(ID3算法)
信息增益指的就是划分可以带来纯度的提高,信息熵的下降。它的计算公式,是父亲节点的信息熵减去所有子节点的信息熵。在计算的过程中,我们会计算每个子节点的归一化信息熵,即按照每个子节点在父节点中出现的概率,来计算这些子节点的信息熵。所以信息增益的公式可以表示为:

ID3的算法规则相对简单,可解释性强。同样也存在缺陷,比如我们会发现ID3算法倾向于选择取值比较多的属性。这种缺陷不是每次都会发生,只是存在一定的概率。在大部分情况下,ID3 都能生成不错的决策树分类。
ID3算法的核心思想:根据样本子集属性取值的信息增益值的大小来选择决策属性(即决策树的非叶子结点),并根据该属性的不同取值生成决策树的分支,再对子集进行递归调用该方法,当所有子集的数据都只包含于同一个类别时结束。最后,根据生成的决策树模型,对新的、未知类别的数据对象进行分类。
ID3算法优点:方法简单、计算量小、理论清晰、学习能力较强、比较适用于处理规模较大的学习问题。
ID3算法缺点:倾向于选择那些属性取值比较多的属性,在实际的应用中往往取值比较多的属性对分类没有太大价值、不能对连续属性进行处理、对噪声数据比较敏感、需计算每一个属性的信息增益值、计算代价较高。
决策树算法的关键在于如何选择最优划分属性。一般而言,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即其纯度越高越好。
通常,使用信息熵(information entropy)来作为度量样本纯度的标准,计算公式为:
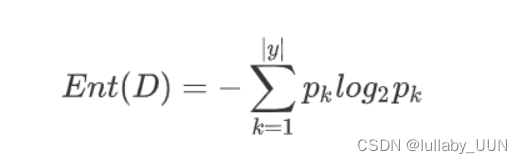
2.2增益率
增益率定义为:
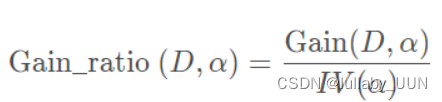
其中
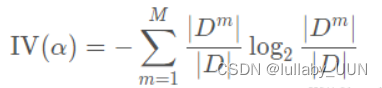
称为属性α的“固有值”.不难发现,属性 α取值数目越多(即M越大),则作为IV(α) 的值通常会越大. 因此,当有些属性取值过多时,可能会导致ID3算法误选取值较多的属性,此时使用增益率作为指标是一个很好的选择,这叫做C4.5决策树.
2.3基尼指数

3.决策树创建及展示(以信息增益划分属性)
现在我们要构建一个睡觉时间、是否运动、是否护肤对皮肤的影响的决策树
数据加载
def createDataSet():
"""
传入要处理的数据集
:return: 数据集内容,数据集标签
"""
dataSet = [[1, 1, 1, 'yes'],
[1, 1, 1, 'yes'],
[0, 1, 1, 'no'],
[1, 0, 1, 'yes'],
[1, 0, 1, 'yes'],
[0, 0, 1, 'no']]
labels = ['十一点前睡觉', '每天运动', '每天护肤']
# print(f'dataset:\n{dataSet}')
return dataSet, labels计算给定数据的香农熵
def calcShanonEnt(dataSet):
"""
计算数据集的信息熵
此处还没有乘权重
:param dataSet:划分好的数据集
:return:子数据集的信息熵,还没有考虑权重进来
"""
# 数据中实例的总数
numEntries = len(dataSet)
# 为数据集所有可能性划分字典
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
# 如果字典中不存在,添加到字典中
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
# 对存在的结果计数
labelCounts[currentLabel] += 1
# print(f'我是labelCounts2:\n{labelCounts}')
# 得到{'yes': 2, 'no': 3}
shannonEnt = 0.0
# 此部分用于计算一个数据集的信息熵,还没有加入权重(不一定是二叉树,有几个key分支就包含几种,这里考虑到了)
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
shannonEnt -= prob * log(prob, 2)
# print(f'我是初始信息熵shannonEnt:\n{shannonEnt}')
return shannonEnt选择最佳属性划分数据集
def chooseBestFeatureToSplit(dataSet):
"""
对于信息熵的计算
:param dataSet:
:return:
"""
# 得到特征数据的长度(特征的个数) 2
numFeatures = len(dataSet[0]) - 1
# 原数据集的信息熵
baseEntropy = calcShanonEnt(dataSet)
# 定义初始的熵增益
bestInfoGain = 0.0;
bestFeature = 0;
for i in range(numFeatures):
# 取某一列特征的值,example在此处代表列 我是featList:[1, 1, 0, 1, 1]
featList = [example[i] for example in dataSet]
# set集合去重取出每一特征下的所有可能情况 我是uniqueVals:{0, 1}
uniqueVals = set(featList)
# 定义一个变量为新的信息熵
newEntropy = 0.0
# 结合上方,按照某一个特征的不同value可以将数据集分割成len(uniqueVals)个子集,分割子数据集,并对子数据集求信息熵
for value in uniqueVals:
subDataSet = spliDataStet(dataSet, i, value)
# print(f'我是subDataSet:\n{subDataSet}')
# 此段代码中,prob是在某一特征分类下的权重,而self.calcShanonEnt函数计算出的为数据集的信息熵
prob = len(subDataSet) / float(len(dataSet))
# 得到的为按某一特征划分后的信息熵
newEntropy += prob * calcShanonEnt(subDataSet)
# 熵增益
infoGain = baseEntropy - newEntropy
# infoGain = newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
# print(f'bestFeature:\n{bestFeature}')
return bestFeature按分类后类别数量排序
def majorityCnt(classList):
# 创建键值为classList中唯一值的数据字典,字典对象存储了classList中每个类标签出现的频率
# 利用operator操作键值排序字典,并返回出现次数最多的分类名称
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# print(f'我是sortedClassCount:\n{sortedClassCount}')
# print(f'我是sortedClassCount:\n{sortedClassCount[0][0]}')
return sortedClassCount[0][0]构建决策树
def createTree(dataSet, labels):
"""
构造树的过程
:param dataSet:
:param labels:
:return:
"""
classList = [example[-1] for example in dataSet]
print(f'我是classList:\n{classList}')
# 递归函数的第一个停止条件是所有的类标签完全相同,则直接返回该类标签
# print(classList.count(classList[0],'==',len(classList)))
# print(classList.count(classList[0]==len(classList)))
if classList.count(classList[0]) == len(classList):
"""
通过打印发现错误,第一个if判断语句的地方没有进来
"""
print('yyyyy', classList[0])
return classList[0]
# 递归函数的第二个停止条件是使用完了所有特征,仍然不能将数据集划分成仅包含唯一类别的分组
elif len(dataSet[0]) == 1:
return majorityCnt(classList)
# print(f'我是classList[0]:\n{classList[0]}')
# return majorityCnt(classList[0])
# if len(dataSet[0]) == 1:
# return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
print(f'bestFeat:\n{bestFeat}')
bestFeatLabel = labels[bestFeat]
print(f'我是bestFeatLabel:\n{bestFeatLabel}')
# 分类结果储存到字典中
myTree = {bestFeatLabel: {}}
# 在标签列表中删除最佳标签
del (labels[bestFeat])
# 得到最佳标签一列的所有可能特征值集合
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
# 遍历特征值集合
for value in uniqueVals:
# 复印列表清单
subLabels = labels[:]
# 递归迭代,逐条插入字典
myTree[bestFeatLabel][value] = createTree(spliDataStet(dataSet, bestFeat, value), subLabels)
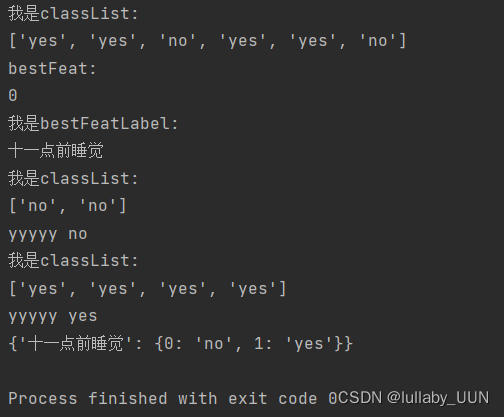
return myTree运行结果
目录