1. Recap
Deep Graph Encoders(深度图编码器)
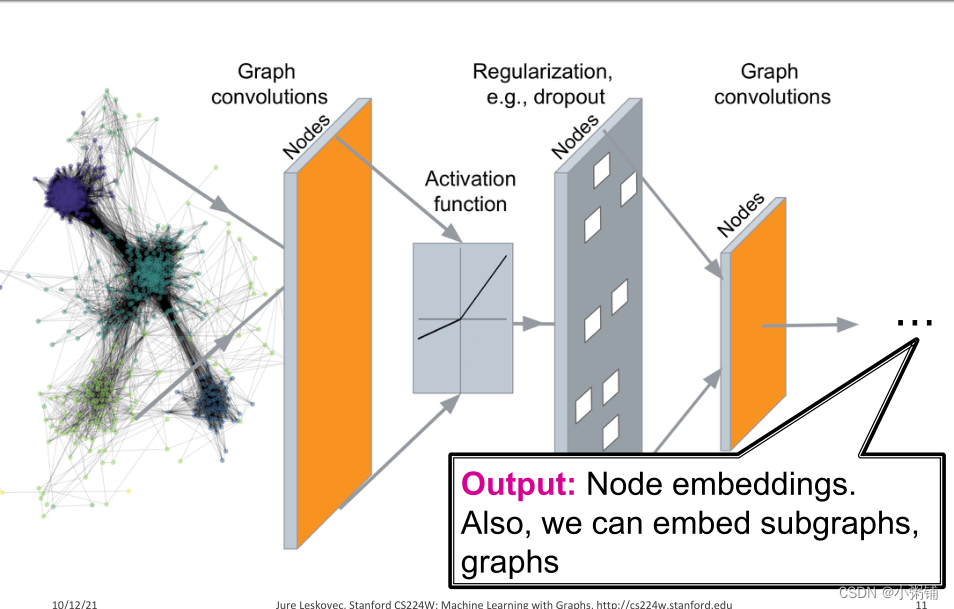
Graph Neural Networks
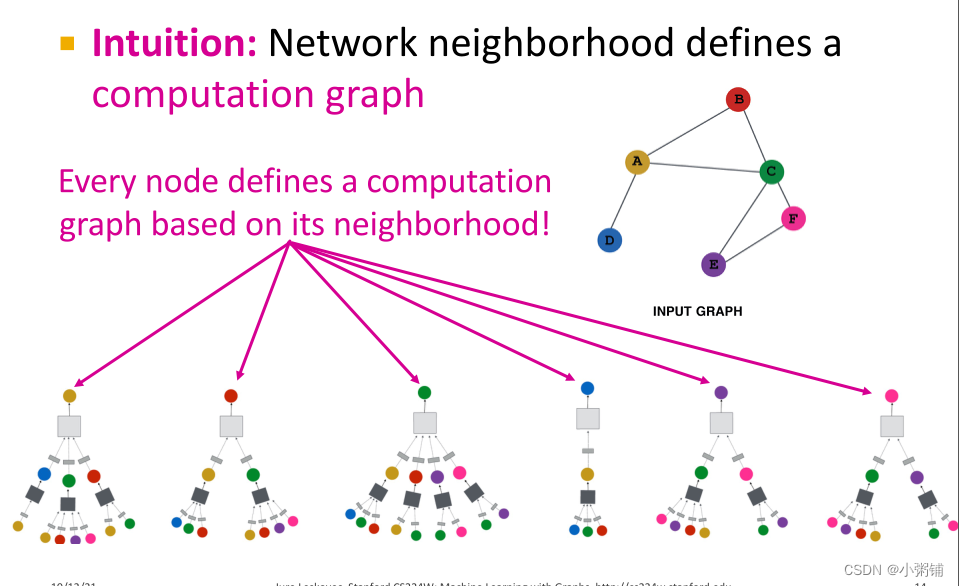
GNN核心思想:节点的邻域定义了一个计算图

Aggregate from Neighbor
想法:节点使用神经网络聚合来自其邻居的信息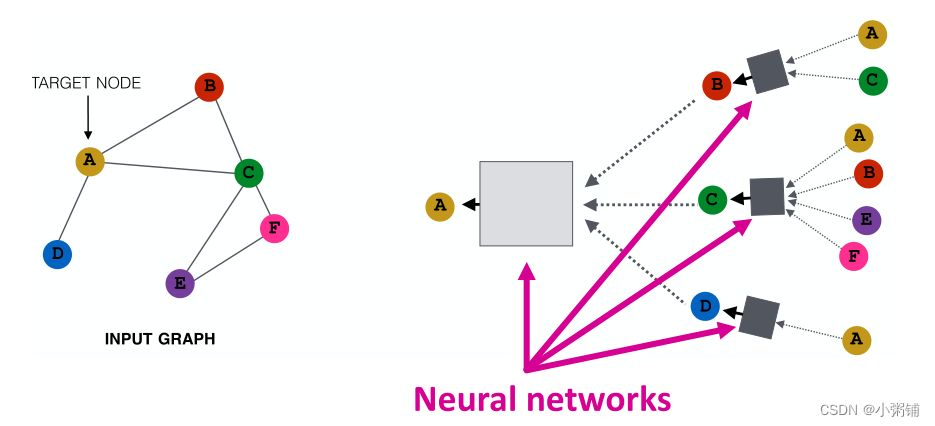
为什么说GNNs泛化了其他神经网络?
因为它定义了置换不变性和等变性的概念。
GNNs VS. CNNs
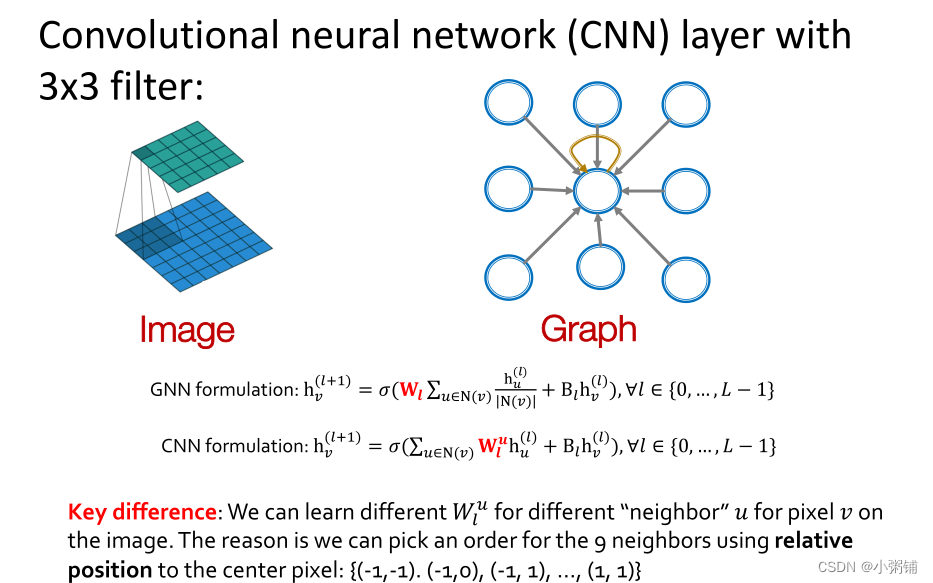
- CNN 可以看作是具有固定邻居大小和排序的特殊 GNN
- CNN的滤波器的大小是预定义的
- GNN 的优点是它能为每个节点处理具有不同度数的任意图
- CNN 不是置换等变的
- 改变CNN像素的顺序会导致不同的输出
GNNs VS. Transformer
Transformer 是最流行的架构之一,它在许多序列建模任务中实现了出色的性能。它的主要机制是self-attention(自我注意力机制):每个标记/单词都通过矩阵计算处理所有其他标记/单词。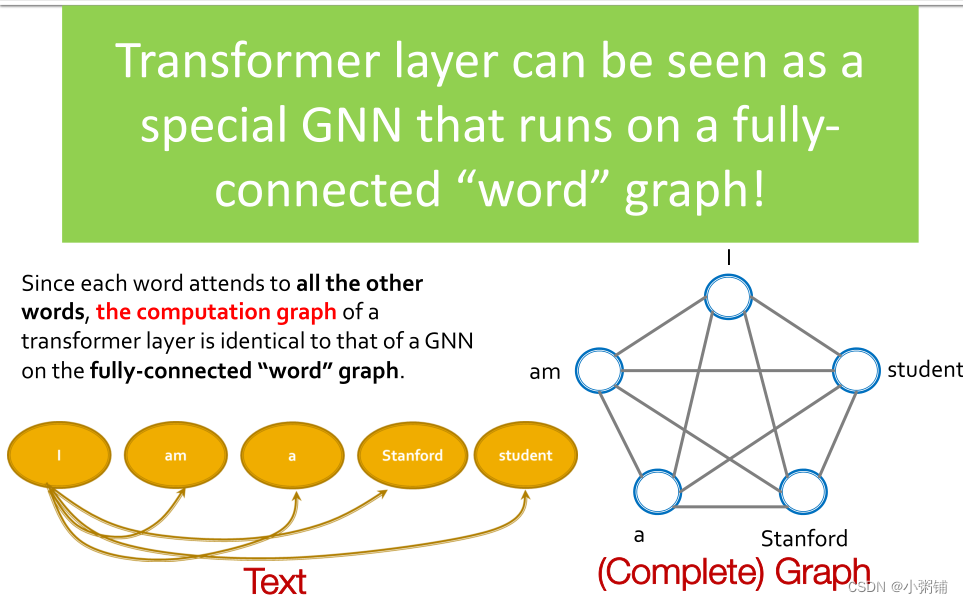
由于每个单词都涉及所有其他单词,因此 Transformer 层的计算图与全连接“单词”图上的 GNN 的计算图相同。Transformer 层可以看作是一个特殊的 GNN,它运行在一个完全连接的“单词”图上。
2. 通用GNN框架
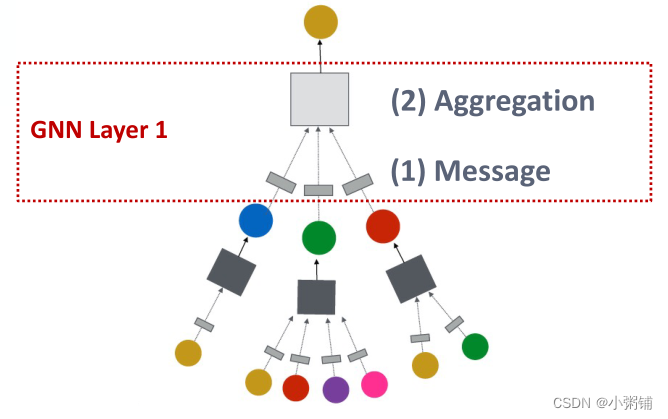
GNN层 = Message + Aggregation
- 在这个视角下可以有不同的架构(实例化)
- 包括GCN, GraphSAGE, GAT, …
- 这些架构的不同之处在于它们如何定义聚合和消息的概念
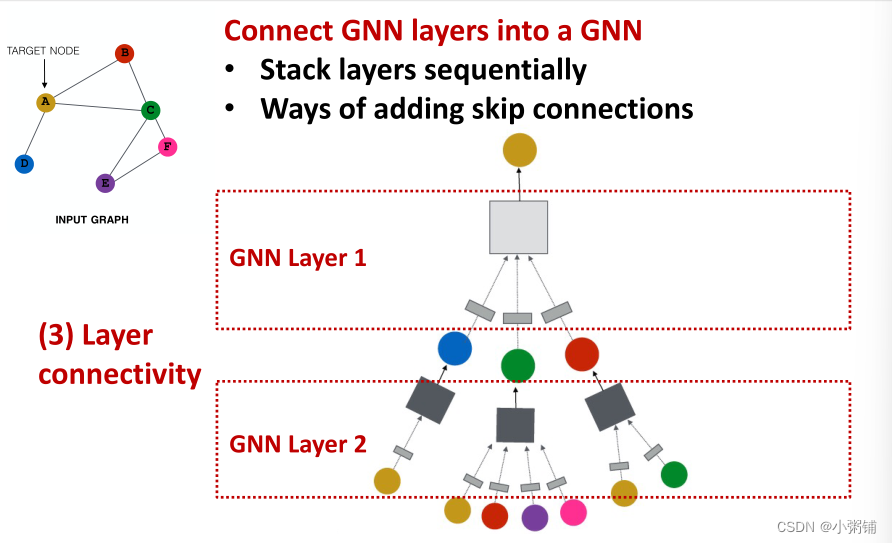
层连通性(Layer connectivity) :我们如何将GNN层连接起来
- 可以按顺序堆叠层
- 也可以添加skip connections
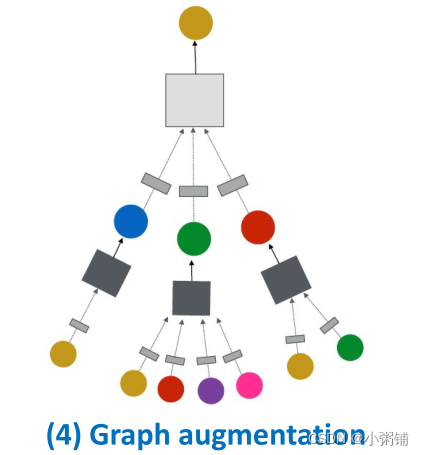
图增强:如何创建计算图?原始输入图≠计算图
- 图特征增强
- 图结构增强
Learning objective
- 我们如何训练GNN:
- 监督/非监督目标
- 节点/边缘/图形级别任务
总体GNN框架如下:

- 我们如何训练GNN:
3. 定义GNN的单个层
GNN层 = Message(消息转换) + Aggregation(消息聚合)

不同的图神经网络架构对这两种操作的定义不同。
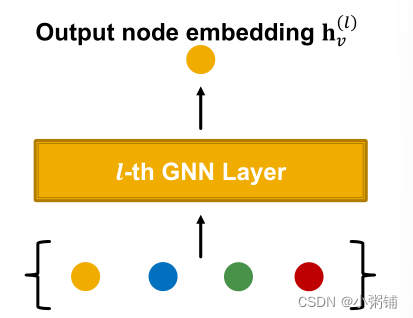
定义GNN层:将一组向量压缩成一个向量
需要两个步骤:
- Message
- Aggregation
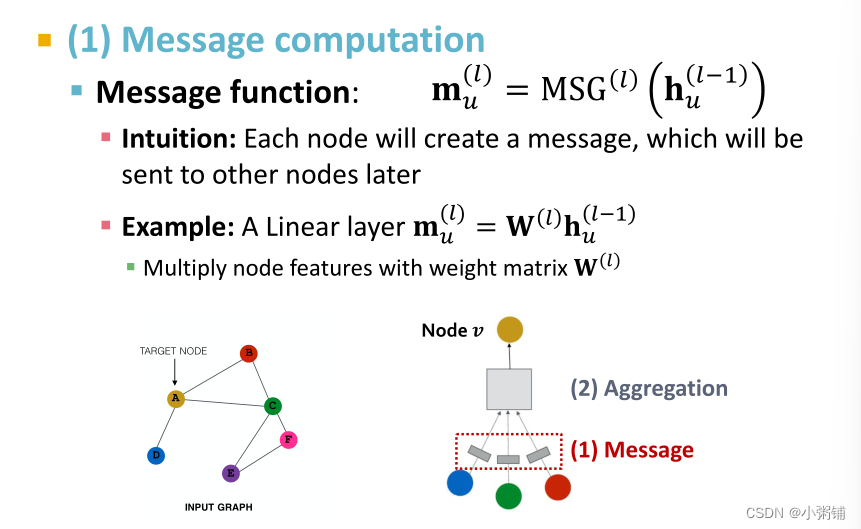
3.1 Message Computation
节点第l层的嵌入是l-1层节点自身的信息和l-1层邻居的信息的聚合,并且这些信息的计算顺序对结果没有影响。
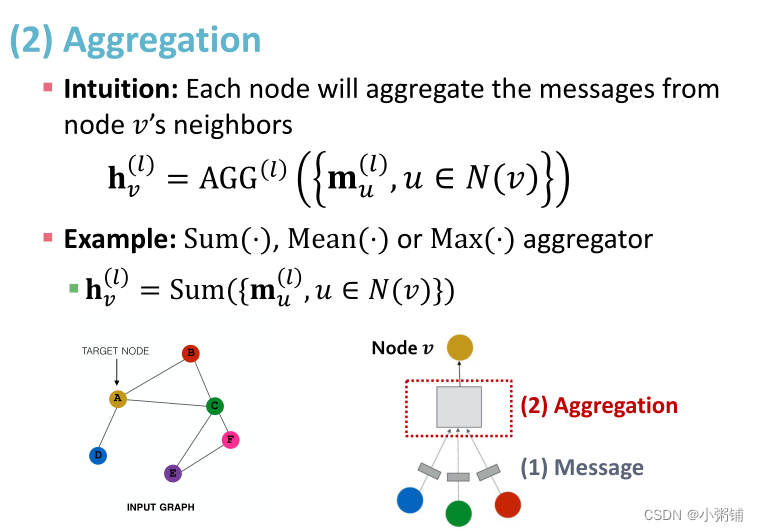
3.2 Message Aggregation
想法:每个节点都要从它的邻域聚合信息,聚合函数可以采用求和、平均或求最大值函数。
问题:采用上面的算法来自节点v本身的节点信息可能会丢失,因为 h v ( l ) h_v^{(l)} hv(l)的计算并不直接依赖于 h v ( l − 1 ) h_v^{(l-1)} hv(l−1)
解决方法:求解第l层的节点嵌入 h v ( l ) h_v^{(l)} hv(l)时,把节点v第l-1层的嵌入 h v ( l − 1 ) h_v^{(l-1)} hv(l−1)也纳入计算:
- Message:计算消息时也考虑来自节点v本身的信息。
- 通常,对于来自节点v自身的消息和来自节点v邻域的消息,我们将执行不同的计算过程。
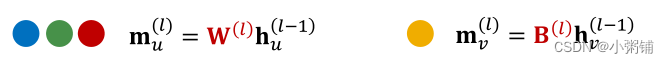
- 通常,对于来自节点v自身的消息和来自节点v邻域的消息,我们将执行不同的计算过程。
- Aggregation:从邻域聚合信息后,我们将聚合来自自身的信息(串联或求和)。

3.3 Summary: A Single GNN Layer

聚合时我们可以加入节点自身的信息,我们还可以把非线性激活函数加入到消息传递或聚合中,以增强网络的表现力。
3.4 经典图神经网络层
1. GCN
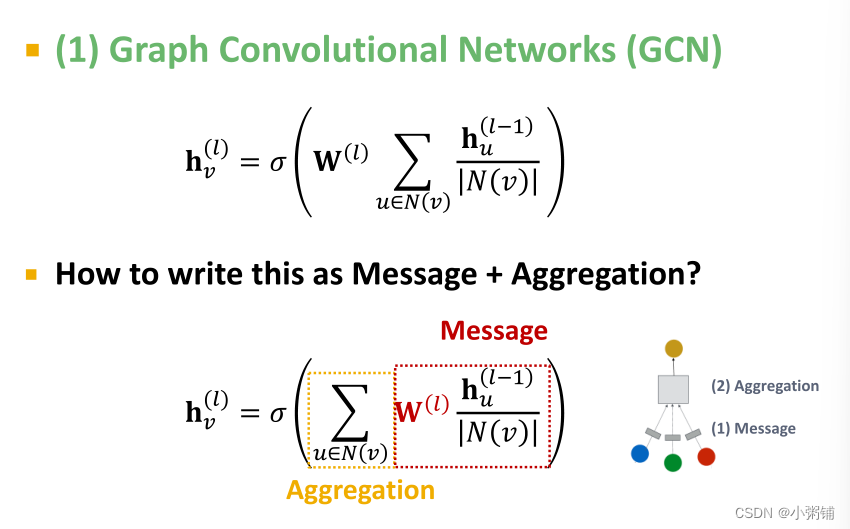
- Message: 将来自邻域的消息和权重矩阵相乘,并用节点度数归一化。
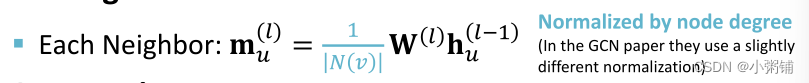
- Aggregation:对来自邻居的消息求和,并应用激活函数
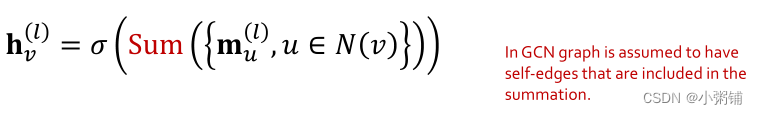
2. GraphSAGE
Message + Aggregation:
- 消息在 A G G ( ⋅ ) AGG(\cdot) AGG(⋅)函数中被计算
- 采用两阶段聚合算法
- Stage 1: 从节点邻居聚合
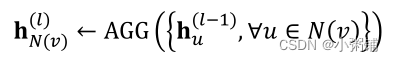
- Stage 2: 进一步聚合节点本身的信息

总过程如下:
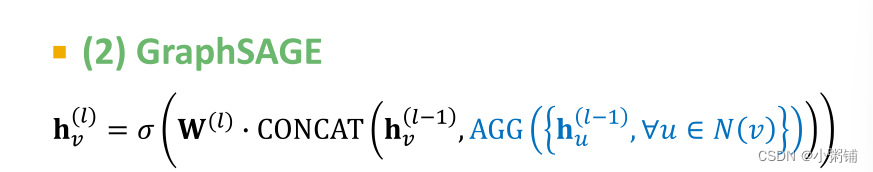
- Stage 1: 从节点邻居聚合
GraphSAGE与GCN的区别:
- 可以采用任意的聚合函数 A G G ( ⋅ ) AGG(\cdot) AGG(⋅)
- 从节点本身获取信息,并对其进行转换,然后将其与聚集的信息连接起来
GraphSAGE Neighbor Aggregation:
可以选择不同的聚合函数:
- Mean:取邻居的加权平均值
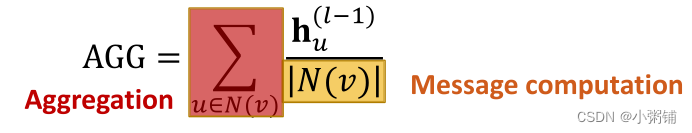
- 池化:变换邻域信息向量(多层感知机)并应用对称向量函数 M e a n ( ⋅ ) Mean(\cdot) Mean(⋅)或 M a x ( ⋅ ) Max(\cdot) Max(⋅) ,

- LSTM:将序列模型LSTM应用于重新排序的邻居(训练模型忽略邻居节点的顺序)

GraphSAGE:L2 Normalization
- 对GraphSAGE的每一层嵌入应用 L 2 L_2 L2 正则化
- h v ← h v ( l ) ∣ ∣ h v ( l ) ∣ ∣ 2 ∀ v ∈ V h_v \leftarrow \frac{h_v^{(l)}}{|| h_v^{(l)}||_2} \forall v \in V hv←∣∣hv(l)∣∣2hv(l)∀v∈V ,其中 ∣ ∣ u ∣ ∣ 2 = ∑ i u i 2 ||u||_2 = \sqrt{\sum_i u_i^2} ∣∣u∣∣2=∑iui2
- 如果不用L2正则化,不同的嵌入向量会有不同的模长,不同的比例
- 在某些情况下(并非总是),嵌入的规范化会提升性能
- L2归一化后,所有的向量都将具有相同的 l 2 − n o r m l_2-norm l2−norm,相同的长度1。
3. GAT
图注意力网络:

在GCN或GraphSAGE中,
- α v u = 1 ∣ N ( v ) ∣ \alpha_{vu} = \frac{1}{|N(v)|} αvu=∣N(v)∣1,是节点 u 的消息对节点 v 的权重因子(重要性)
- α v u \alpha_{vu} αvu是根据图的结构属性(节点度)显式定义的
- 所有邻居 u ∈ N ( v ) u \in N(v) u∈N(v)对节点v都是同等重要的
然而在图注意力网络中,并非所有节点的邻居都同等重要 - 注意力受到认知注意力的启发
- 注意力 α v u \alpha _{vu} αvu专注于输入数据的重要部分而忽略其余部分。
- 理念:神经网络应该在数据的那个小而重要的部分上投入更多的计算能力
- 数据的哪一部分更重要取决于上下文,是通过训练学习的
GAT(图注意力网络)
目标:指定图中每个节点的不同邻居的任意重要性
理念:按照注意力策略计算图中每个节点的嵌入 h v ( l ) h_v^{(l)} hv(l),为邻域中的不同节点隐式指定不同的权重
注意力机制:
- 让 α v u \alpha_{vu} αvu作为注意力机制a的副产品被计算出来
- (1) a 根据节点 u,v 的信息,计算各对节点的注意力系数 e v u e_{vu} evu, e v u e_{vu} evu表示节点u的信息对节点v的重要性。

- 将 e v u e_{vu} evu归一化为最后的注意力权重 α v u \alpha_{vu} αvu
- 我们使用softmax函数,这样所有权重的和为1: ∑ u ∈ N ( v ) α v u = 1 \sum_{u\in N(v)}\alpha_{vu} = 1 ∑u∈N(v)αvu=1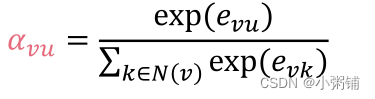
- 基于最终注意力权重 α v u \alpha_{vu} αvu的加权和:
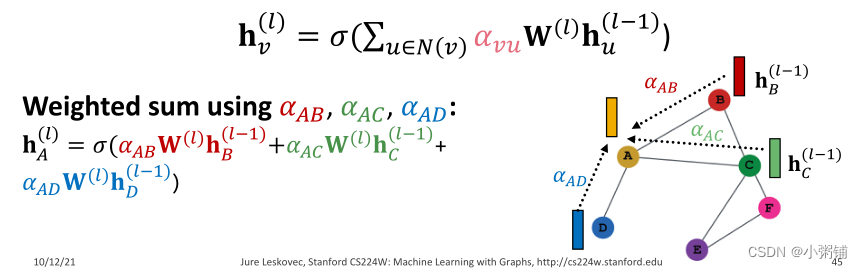
- (1) a 根据节点 u,v 的信息,计算各对节点的注意力系数 e v u e_{vu} evu, e v u e_{vu} evu表示节点u的信息对节点v的重要性。
- 注意力机制 a 的形式
- 注意力机制的形式与注意力机制 a 的选择无关
- 例如,我们使用一个简单的单层神经网络
- a具有可训练的参数(线性层中的权重)
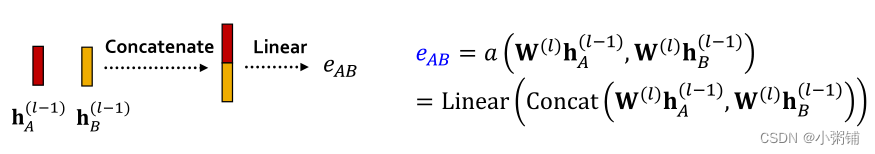
- a具有可训练的参数(线性层中的权重)
- 例如,我们使用一个简单的单层神经网络
- a 的参数是联合训练的
-以端到端的方式学习注意力机制的参数和权重矩阵(即神经网络 W ( l ) W^{(l)} W(l) 的其他参数)
- 注意力机制的形式与注意力机制 a 的选择无关
- 多头注意力机制 ( Multi-head) :可以稳定注意力机制的学习过程
- 创建多个注意力分数(每个副本具有不同的参数集)

- 然后再将输出汇总:
- 串联或求和
我们随机初始化 α v u 1 , α v u 2 , α v u 3 \alpha_{vu}^1, \alpha_{vu}^2, \alpha_{vu}^3 αvu1,αvu2,αvu3这三个参数, 并采用不同的函数进行训练,最后这三个数都会收敛到一个局部最小值,但是由于我们使用了多个注意力头,我们将它们的转化平均在一起,这会使得我们的模型更加健壮,而不致于卡在优化空间的某些怪异点。
- 串联或求和
- 创建多个注意力分数(每个副本具有不同的参数集)
注意力机制的好处 (不太能理解,看一下这个模型的代码后再回来看一下):
- 核心优势:允许(隐式地)为不同的邻居指定不同的重要性值( α v u ) \alpha_{vu}) αvu)
- 计算效率高
- 注意力系数的计算可以在图的所有边上并行化
- 聚合可以在所有节点上并行化
- 储存效率高
- 稀疏矩阵运算不需要存储超过 O ( V + E ) O(V + E) O(V+E)的实体
- 固定数量的参数,与图大小无关
- 注意力机制是局部的
- 只有本地网络社区参与
- 归约能力(Inductive capability)
- 一种共享的边缘机制
- 不依赖于全局图结构
4. 实践中的 GNN 层
- 在实践中,这些经典的 GNN 层是一个很好的起点:
- 通常可以通过考虑通用的 GNN 层设计来获得更好的性能
- 具体来说,我们可以包括现代深度学习模块,这些模块被证明在许多领域都很有用。

- 许多现代深度学习模块可以合并到 GNN 层中,例如:
- 批量标准化(Batch Normalization):可以稳定神经网络的训练过程
- Dropout:避免过拟合
- 注意力或门控机制(Attention/Gating):可以控制消息的重要性
- 以及其他任何有用的深度学习模块
4.1 批量归一化
目标:稳定神经网络训练过程
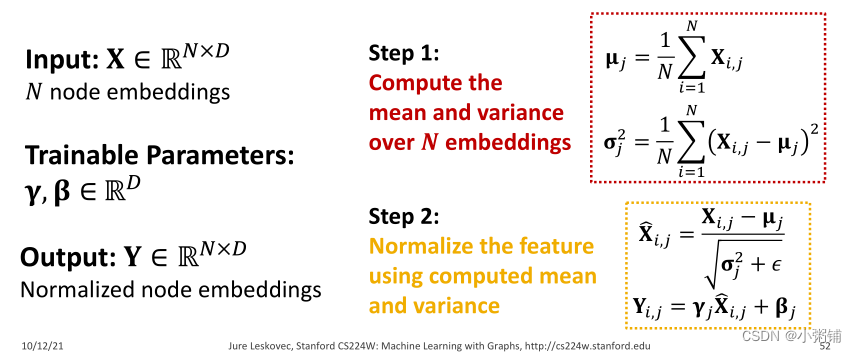
核心思想:给定一批输入(节点嵌入)
- Re-center:使节点嵌入的均值为0
- Re-scale:使节点嵌入的方差为1
步骤:
- step1:计算N个嵌入的均值和方差
- step2:使用计算出的平均值和方差对特征进行归一化处理
4.2 Dropout
目标:对神经网络进行规范化处理以防止过度拟合。
想法:
- 在训练期间,以一定的概率p,随机将神经元设置为零(关闭)
- 在测试期间:使用所有神经元进行计算
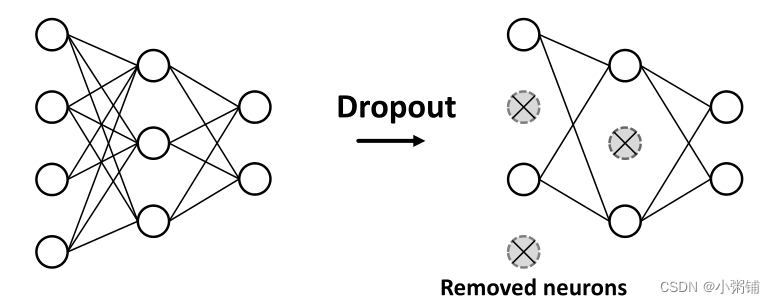
这样,我们可以使神经网络模型对噪音有更强的抵抗力,防止其过度拟合。
在 GNN 中,Dropout 应用于消息函数中的线性层: - 一个带有线性层的简单消息函数如下:
m u ( l ) = W ( l ) h u l − 1 m_u^{(l)} = W^{(l)}h_u^{l-1} mu(l)=W(l)hul−1

4.3 激活函数(非线性)
将激活应用于嵌入 x x x的第 i i i维:

总结:现代深度学习模块可以包含在 GNN 层中以获得更好的性能,设计新颖的 GNN 层仍然是一个活跃的研究前沿,您可以探索不同的 GNN 设计或在 GraphGym 中尝试自己的想法。
5. GNN层间的堆叠
5.1 如何将 GNN 层连接成 GNN?
- 按顺序堆叠层
- 添加skip连接的方法
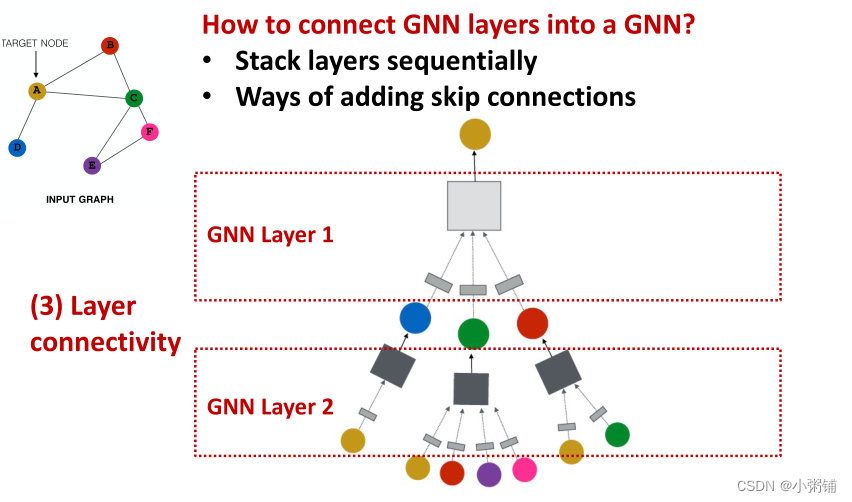
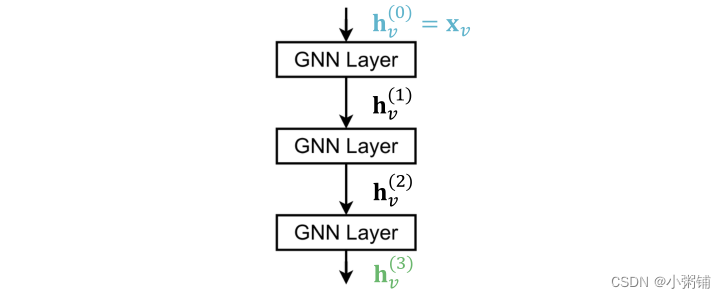
如何构建图神经网络? - 标准方式:按顺序堆叠 GNN 层
- 输入:初始原始节点特征 x v x_v xv
- 输出:节点嵌入 h v ( L ) h_v^{(L)} hv(L)在 K 个 GNN 层之后
5.2 过度平滑问题
过度平滑问题:堆叠许多 GNN 层会造成过度平滑问题,即所有节点嵌入收敛到相同的值,这导致我们不能使用节点嵌入来区分节点。
5.2.1 为什么会出现过度平滑问题:
- 感受野:节点v的感受野就是决定节点v的最终嵌入的一组节点
在 K 层 GNN 中,每个节点都有一个K-跳邻域的感受野
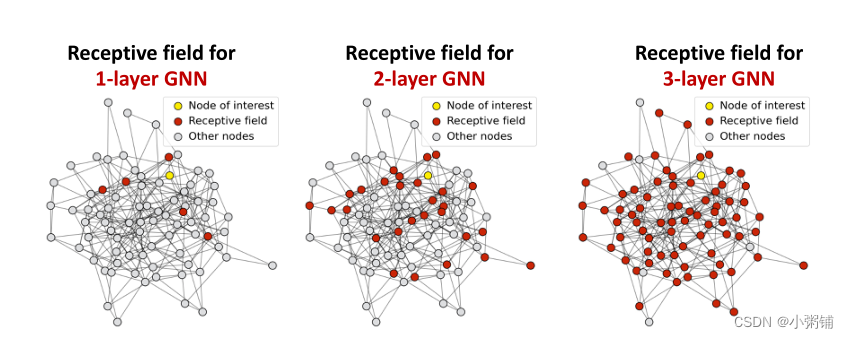
- 两个节点的感受场重叠:当我们增加跳数(GNN层的数量)时,共享邻居迅速增长

- 我们可以通过感受野的概念来解释过度平滑的问题:
- 一个节点的嵌入是由它的感受野决定的
- 如果两个节点具有高度重叠的感受野,那么它们的嵌入高度相似
- 逻辑链:堆叠许多 GNN 层 -> 节点将具有高度重叠的感受野 -> 节点嵌入将高度相似 -> 遭受过平滑问题
5.2.2 如何解决过平滑问题?:设计 GNN 层连接性(Connectivity)
1. 尽量少添加 GNN 层时,并提高GNN层的表达能力
- 与其他领域的神经网络(用于图像分类的 CNN)不同, GNN 层并不是越多越好
- Step 1:分析解决问题所必要的感受野。例如,通过计算图的直径
- Step 2:将 GNN 层数 L 设置为比我们喜欢的感受野多一点,但不是没必要的大
GNN层数变少了,那我们如何提高浅层 GNN 的表达能力呢?
- 方法1:提高每个GNN层内的表达能力
- 在我们之前的例子中,每个转换或聚合函数只包括一个线性层
- 我们可以增加层数,使聚合/转换成为一个深度神经网络,在下图中,消息转换和消息聚合操作都可以包含一个三层的感知机:
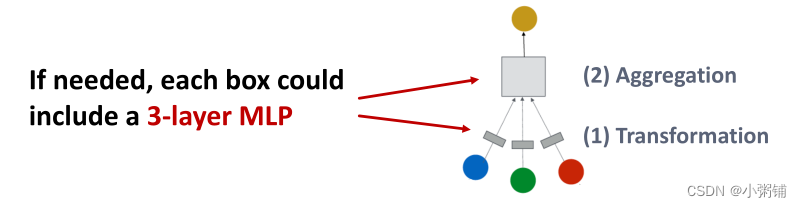
- 方法2:添加不传递信息的层
- 一个GNN不一定只包含GNN层 ,例如,我们可以在GNN层之前和之后添加MLP层(应用于每个节点),作为前处理层和后处理层

- 前处理层:当有必要对节点特征进行编码时非常重要。例如,当节点为图像/文本时
- 后处理层:当需要对节点嵌入进行推理/转换时非常重要 ,例如,图分类、知识图等
- 实践证明,添加这些层的效果很好
- 一个GNN不一定只包含GNN层 ,例如,我们可以在GNN层之前和之后添加MLP层(应用于每个节点),作为前处理层和后处理层
2. 在GNNs中添加skip connections
如果分析了感受野之后,发现问题仍然需要许多GNN层,那我们如果解决多层GNN的过平滑问题呢?
解决方案:使用跳转链接(skip connections)。
Veit et al. Residual Networks Behave Like Ensembles of Relatively Shallow Networks, ArXiv 2016
- 从过度平滑中观察到:早期GNN层中的节点嵌入有时可以更好地区分节点
- 解决方案:我们可以通过在GNN中添加捷径(shortcuts) 来增加早期层对最终节点嵌入的影响
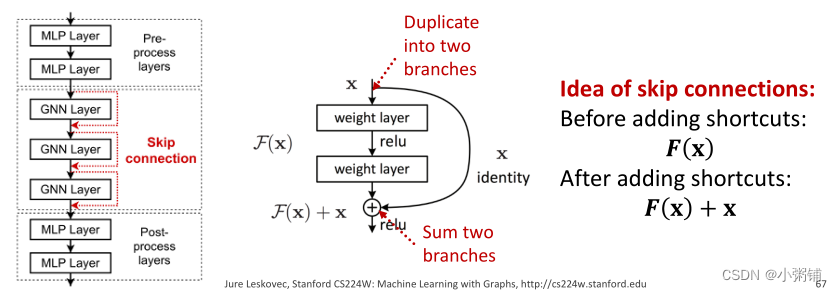
为什么跳转连接能起作用呢?
- 直觉:跳转链接创造了一个混合模型
- N个跳转链接就会有 2 N 2^N 2N次方个可能的路径
- 每条路径最多可以有N个模块
- 我们自动得到一个浅层GNN和深层GNN的混合模型

Example: GCN with Skip Connections

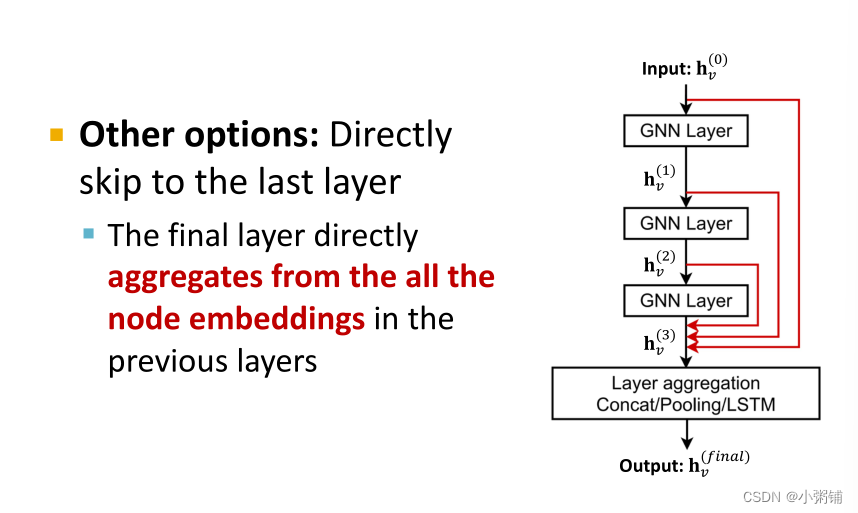
另一种类型的跳转链接:直接跳到最后一层,最后一层直接聚合了前几层的所有节点嵌入。