一、整形在内存中的存储
数据在内存中是以二进制补码的形式存储的 。下面来介绍原码、反码、补码的概念。
正数的原码、反码、补码相同。
负数求值如下:
原码
直接将数值按照正负数的形式翻译成二进制就可以得到原码。
反码
将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码
反码 +1 就得到补码。

eg:
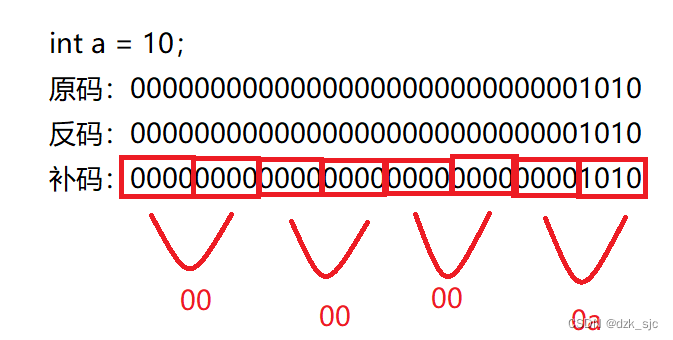

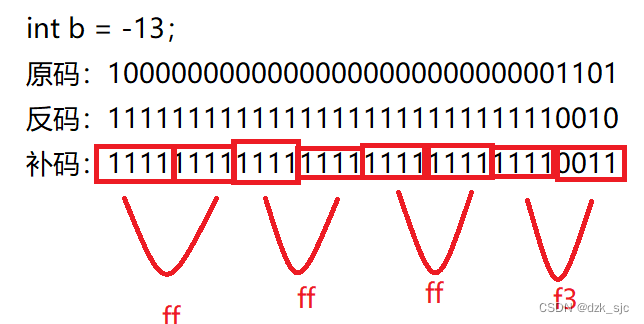

由上图可知:整形在内存中是以补码的形式存储的,但是实际在内存中的顺序是不一样的。
原因是:按照小端存储的,什么是小端?

由图可知小端为:二进制底权放入低地址处高权放在高地址处。
但是取出用的时候是二进制补码
既然了解了小端,那么大端又是怎么样的呢?
大端与小端相反,它是底权放入高地址处高权放在低地址处。
二、浮点数在内存中的存储
任意一个二进制浮点数V可以写成如下形式:
(-1)^S * M * 2^E
(-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
M表示有效数字,大于等于1,小于2。
2^E表示指数位。
以浮点数5.5何-5.5为例:

IEE754规定:
32位的时候是这样存储的:

64位的时候是这样存储:

S、E、M的值又是怎么确定的呢?
M是去掉小数点前面的一保留小数点后面的二进制数。为什么这么做呢?
答:是节省 1 位有效数字。以 32 位
浮点数为例,留给 M 只有 23 位,
将第一位的 1 舍去以后,等于可以保存 24 位有效数字,这样就可以更精确了。
IEEE754规定 :1<= M <2 。
对于E的在内存中的存储比较麻烦。
首先, E 为一个无符号整数( unsigned int )
这意味着,如果 E 为 8 位,它的取值范围为 0~255 ;如果 E 为 11 位,它的取值范围为 0~2047 。
但是,我们 知道,科学计数法中的E 是可以出 现负数的,所以IEEE 754 规定,存入内存时 E 的真实值必须再加上一个中间数,对于 8 位的 E ,这个中间数 是127 ;对于 11 位的 E ,这个中间 数是1023 。
比如,2^3 的 E 是3 ,所以保存成 32 位浮点数时,必须保存成3 +127=130 ,即 10000010。
取出又分为三种情况:
E 不全为 0 或不全为 1
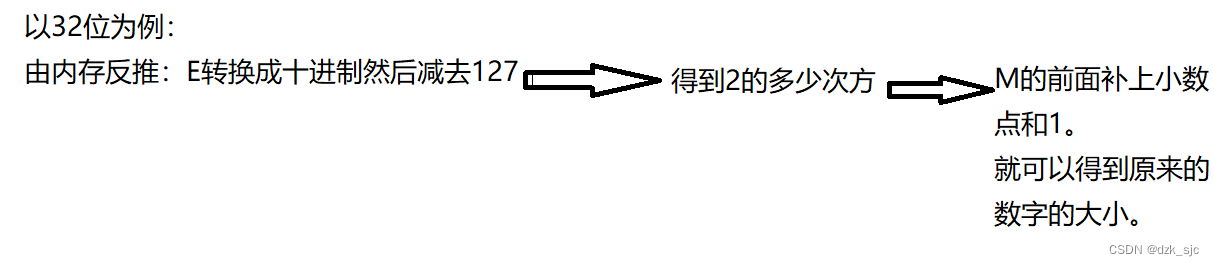
E 全为 0
这时,浮点数的指数 E 等于 1-127 (或者 1-1023 )即为真实值,
有效数字 M 不再加上第一位的 1 ,而是还原为 0.xxxxxx 的小数。这样做是为了表示 ±0 ,以及接近于
0 的很小的数字。
0 01111110 00000000000000000000000
E 全为 1
这时,如果有效数字 M 全为 0 ,表示 ± 无穷大(正负取决于符号位 s );
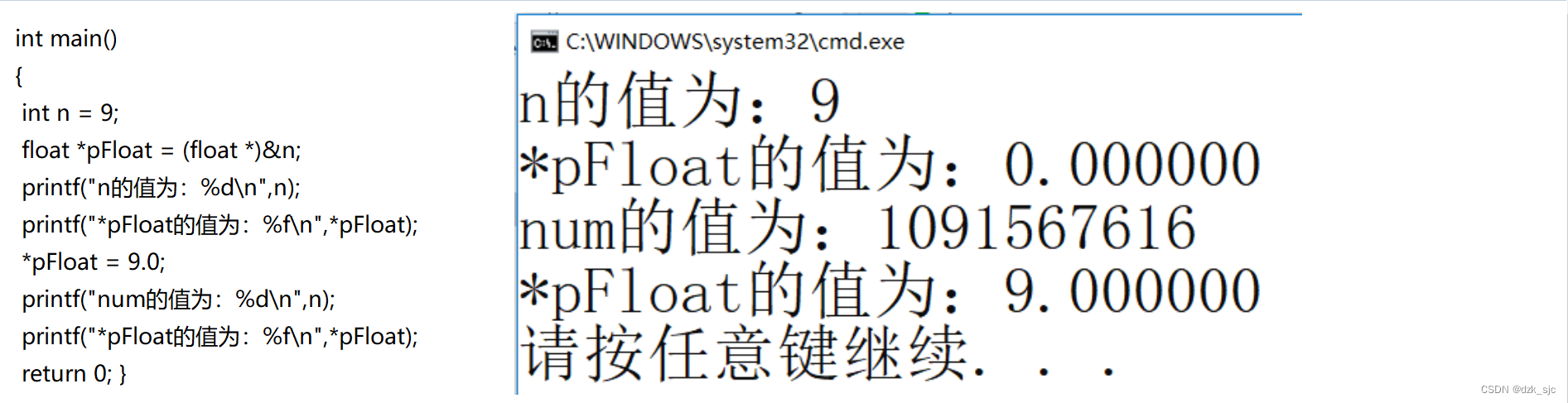
看下面的例题:

本文含有隐藏内容,请 开通VIP 后查看