9--RNN

有隐藏状态的循环神经网络

        假设在时间步t有小批量输入，即对于n个序列样本的小批量，的每一行对应于来自该序列的时间步t处的一个样本，用表示时间步t的隐藏变量。与MLP不同的是， 我们在这里保存了前一个时间步的隐藏变量，并引入了一个新的权重参数。当前时间步隐藏变量由当前时间步的输入与前一个时间步的隐藏变量一起计算得出：

        从相邻时间步的隐藏变量和之间的关系可知， 这些变量捕获并保留了序列直到其当前时间步的历史信息， 就如当前时间步下神经网络的状态或记忆， 因此这样的隐藏变量被称为隐状态（hidden state）。对于时间步t，输出层的输出类似于多层感知机中的计算：

        其实循环神经网络与MLP不同的地方就在于，中间隐藏层的更新会依赖于上一时间步的隐藏层。（下图中蓝色的点为隐藏层）

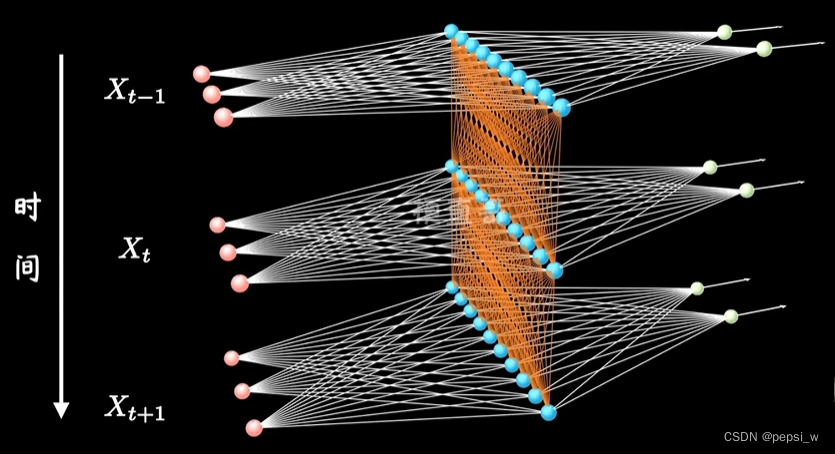
基于循环神经网络的字符级语言模型 

        根据过去的词与当前的词来对下一个词进行预测，可以将词的原始序列位移一个词源作为一个标签。考虑使用神经网络来进行语言建模，设小批量大小为1，批量中的那个文本序列为“machine”。这里考虑字符级语言模型，下图展示了如何通过之前以及当前字符预测下一个字符。

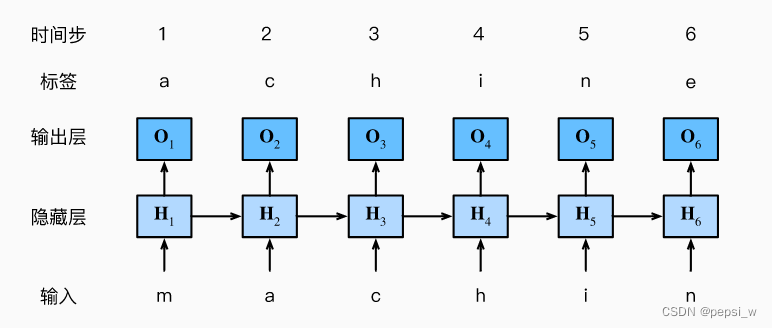
        在训练过程中，对每个时间步的输出都进行一个softmax操作，并利用交叉熵损失计算模型输出和标签之间的误差。

困惑度（Perplexity）

        对于语言模型预测的结果，通过计算序列的似然概率来度量模型的质量。 一个更好的语言模型应该能更准确地预测下一个词元。因此，它在压缩序列时花费更少的比特。所以可以通过一个序列中所有的n个词元的交叉熵损失的平均值来衡量：

        其中P由语言模型给出， xt是在时间步t从该序列中观察到的实际词元，上式的指数则称为困惑度，即下一个词元的实际选择数的调和平均数

        在最好的情况下，模型总是完美地估计标签词元的概率为1（即预测结果为一个词元）， 在这种情况下，模型的困惑度为1。 在最坏的情况下，模型总是预测标签词元的概率为0，在这种情况下，困惑度是正无穷大。在基线上，该模型的预测是词表的所有可用词元上的均匀分布，困惑度等于词表中唯一词元的数量。

实例

        基于时光机器数据集来训练模型，具体代码如下:

!pip install git+https://github.com/d2l-ai/d2l-zh@release  # installing d2l
!pip install matplotlib_inline
!pip install matplotlib==3.0.0

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size , num_steps = 32,35
train_iter,vocab = d2l.load_data_time_machine(batch_size , num_steps)

#构造一个具有256个隐藏单元的单隐藏层的循环神经网络层
num_hiddens = 256
rnn_layer = nn.RNN(len(vocab),num_hiddens,1)


class RNNModel(nn.Module):
  def __init__(self,rnn_layer,vocab_size,**kwargs):
    super(RNNModel,self).__init__(**kwargs)
    self.rnn = rnn_layer
    self.vocab_size = vocab_size
    self.num_hiddens = self.rnn.hidden_size
    if not self.rnn.bidirectional:
      self.num_directions=1
      self.linear = nn.Linear(self.num_hiddens,self.vocab_size)
    else:
      self.num_directions=2
      self.linear = nn.Linear(self.num_hiddens*2,self.vocab_size)
  def forward(self,inputs,state):
    X = F.one_hot(inputs.T.long(),self.vocab_size)
    X = X.to(torch.float32)
    Y, state = self.rnn(X,state)
    output = self.linear(Y.reshape(-1,Y.shape[-1]))
    return output,state
  #初始化隐状态为0 形状是（隐藏层数，批量大小，隐藏单元数）
  def begin_state(self,device,batch_size=1):
    if not isinstance(self.rnn,nn.LSTM):
      return  torch.zeros((self.num_directions * self.rnn.num_layers,
                    batch_size, self.num_hiddens),device=device)
    else:
       return (torch.zeros((self.num_directions * self.rnn.num_layers,
                batch_size, self.num_hiddens), device=device),
            torch.zeros((self.num_directions * self.rnn.num_layers,
                batch_size, self.num_hiddens), device=device))
device = d2l.try_gpu()
net = RNNModel(rnn_layer,vocab_size=len(vocab))
num_epochs,lr = 500,1
d2l.train_ch8(net,train_iter,vocab,lr,num_epochs,device)

        运行结果如下，500个epoch后困惑度达到了1.3。

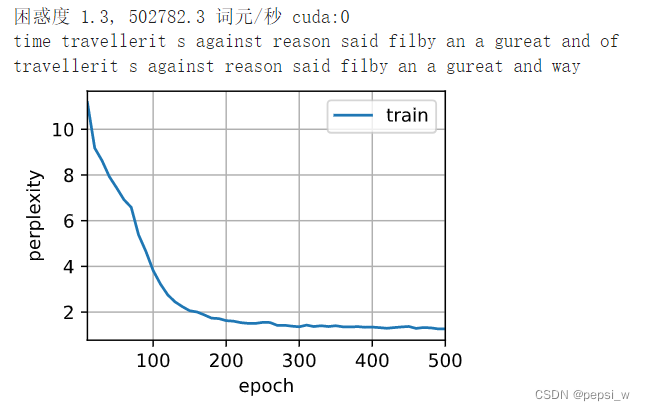
        另外，这里分别使用训练前和训练后的模型对“time traveller”后续词元进行续写，可以看出模型训练前完全是随机性的预测字符串，虽然训练后的模型预测结果语义上不太通顺，但预测出来的单词大部分是正确的（该模型的词元是字符）。