MIT6.005 Problem Set 0 Turtle Graphics

课程网站：https://ocw.mit.edu/ans7870/6/6.005/s16/

初始化Git仓库

在课程网站下载代码文件夹ps0.zip并解压，然后到解压后的文件夹处打开git bash：

输入：

git init

如下所示：

热身

按照课程所说的代码使用规则来实现一个判断代码可不可以用在你的作业中的函数，我也懒得看他的规则了，就随便写了一下，通过了测试。

public static boolean mayUseCodeInAssignment(boolean writtenByYourself,
        boolean availableToOthers, boolean writtenAsCourseWork,
        boolean citingYourSource, boolean implementationRequired) {
    return writtenByYourself || 
            (!availableToOthers) || 
             writtenAsCourseWork || 
              citingYourSource || 
               implementationRequired;
}

提交：

打开git bash，输入git status，检查各个文件的状态，由于之前还没有添加过，因此现在还是空的：

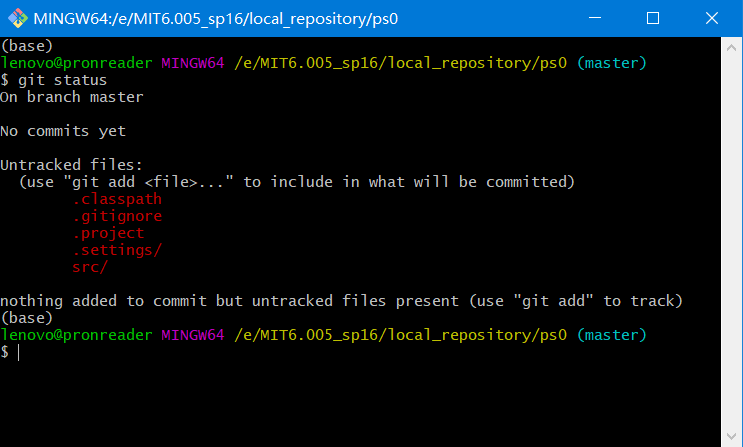
输入git diff，检查改变，由于之前还没有提交过，因此没有改变：

输入git add src/rules/RulesOf6005.java进行暂存：

输入git commit进行提交：

Turtle graphics and the Logo language

实现一个在图形化界面上画线的小程序。

函数实现：

drawSquare：

这个函数绘制一个正方形，简单了解一下forward和turn函数后实现这个函数还是比较简单的：

public static void drawSquare(Turtle turtle, int sideLength) {
    int DEGREES_TO_VERTICAL = 90;
    for (int i = 0; i < 4; ++i) {
        turtle.forward(sideLength);
        turtle.turn(DEGREES_TO_VERTICAL);
    }
}

calculateRegularPolygonAngle：

根据边数算角度

public static double calculateRegularPolygonAngle(int sides) {
    return 180.0 * (sides - 2) / sides;
}

drawRegularPolygon：

画多边形，与前面的画正方形类似

public static void drawRegularPolygon(Turtle turtle, int sides, int sideLength) {
    double degrees = 180 - calculateRegularPolygonAngle(sides);
    for (int i = 0; i < sides; ++i) {
        turtle.forward(sideLength);
        turtle.turn(degrees);
    }
}

calculateHeadingToPoint：

计算开始方向的方向向量$\vec{a}$与目标方向的方向向量$\vec{b}$沿顺时针方向从$\vec{a}$到$\vec{b}$的夹角：

• 通过$cos\theta =\frac{\vec{a}\cdot \vec{b}}{|\vec{a}|\cdot |\vec{b}|}$，计算$cos\theta$值
• 通过$arccos$计算得$\theta$
• 注意此时的$\theta$可能是沿逆时针的角，因此需要一步校验，将$\vec{a}$顺时针旋转$\theta$度，若旋转后与$\vec{b}$夹角为$0$，则返回$\theta$，否则返回$360-\theta$。

public static double calculateHeadingToPoint(double currentHeading, int currentX, int currentY, int targetX, int targetY) {
    double r = Math.toRadians(currentHeading);
    // 向量a, 设长度为1，方便计算
    double[] v1 = { Math.sin(r), Math.cos(r) };

    double dx = targetX - currentX, dy = targetY - currentY;
    // 向量b
    double[] v2 = {dx, dy};
    // v2的长度
    double length2 = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2));
    // 夹角theta的cos
    double cosTheta = (v1[0] * v2[0] + v1[1] * v2[1]) / length2;
    // arccos求角度得弧度制结果
    double theta = Math.acos(cosTheta);
    // 旋转a
    double[] v1s = {Math.sin(r + theta), Math.cos(r + theta)};
    // 求v1s与v2的夹角dt来判断theta是否为真正结果
    double cosdt = (v1s[0] * v2[0] + v1s[1] * v2[1]) / length2;
    double Dtheta = Math.toDegrees(theta);
    // 不直接判断是否等于1，保证精度不影响结果
    return (Math.abs(cosdt - 1) < 0.001) ? Dtheta : 360 - Dtheta;
}

calculateHeadings：

计算一段路径上每个节点处头要旋转的角度，调用上面的calculateHeadingToPoint就可以了：

public static List<Double> calculateHeadings(List<Integer> xCoords, List<Integer> yCoords) {
    List<Double> list = new ArrayList<>();
    int size = xCoords.size();
    double heading = 0.0;
    for (int i = 0; i < size - 1; ++i) {
        double dtheta = calculateHeadingToPoint(heading, xCoords.get(i), yCoords.get(i), xCoords.get(i + 1), yCoords.get(i + 1));
        list.add(dtheta);
        heading += dtheta;
    }
    return list;
}

drawPersonalArt：

最后，自由发挥，进行绘画，我的实现：

public static void drawPersonalArt(Turtle turtle) {
    turtle.color(PenColor.RED);
    for (int i = 0; i < 75; ++i) {
        turtle.forward(200);

        turtle.turn(175);
    }
}

运行如下：