(16条消息) Pytorch框架的学习(1)_An efforter的博客-CSDN博客
目录
5.Pytorch与张量的操作(裁剪、索引与数据筛选,组合与拼接、切片、变形、填充)
(1条消息) Pytorch框架的学习(1)_An efforter的博客-CSDN博客
(1条消息) Pytorch框架的学习(3)_An efforter的博客-CSDN博客
一、tensor函数的调用
1.Tensor中统计学相关的函数

import torch
a=torch.rand(2,2)
print(a)
print(torch.mean(a))
print(torch.sum(a))
print(torch.prod(a))
print(torch.max(a))
print(torch.min(a))
print(torch.argmax(a,dim=0))#最大值的索引对印的是0.5554与0.2172
print(torch.argmin(a,dim=0))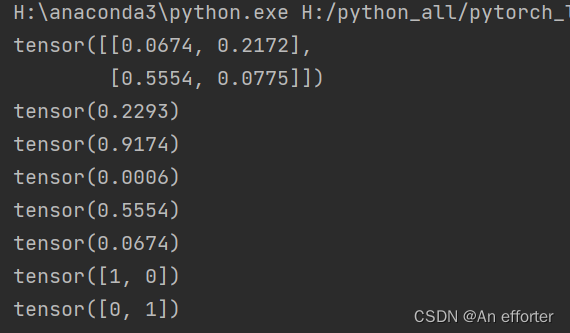

import torch
a=torch.rand(2,2)*10
print(a)
print(torch.std(a))
print(torch.var(a))
print(torch.median(a))
print(torch.mode(a))
print(torch.histc(a,6,0,0)) #直方图函数的使用
#a是数据,6代表6个块,最大值,最小值,默认是0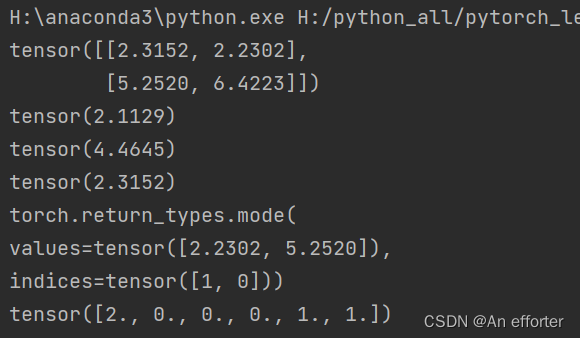
#bincount只能处理1维的数据,可以用于统计某一类别样本的个数
b=torch.randint(0,100,[10])
print(b)
print(torch.bincount(b)) #列表从0-9代表的值出现的频率
2.统计学习中分布函数(以后学习)
- distributions包含可参数化的概率分布和采样函数
得分函数
强化学习中策略梯度方法的基础
pathwise derivative估计器
变分自动编码器中的重新参数化技巧
3.Tensor中的随机抽样
定义随机种子
torch.manual_seed(seed)
定义随机数满足的分布
torch.normal()
import torch
torch.manual_seed(1)
mean=torch.rang(1,2)
std=torch.rang(1,2)
print(torch.normal(mean,std))torch.manual_seed(1)能够约束随机数。

在运行一次也是这个数。如果不加torch.manual_seed(),每一次运行都是随机的数。
4.Pytorch与线性代数运算
(1).Tensor中的范数运算:
- 在泛函分析中,它定义在赋范线性空间中,并满足一定的条件,即①非负性;②齐次性;③三角不等式。
- 常被用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
0范数/1范数/2范数/p范数/核范数:
- torch.dist(input, other, p=2)计算p范数
- torch.norm()计算2范数

p等于几就是几范数, 其中2范数就是欧式距离。
import torch
a=torch.rand(1,2)
b=torch.rand(1,2)
print(a,b)
print(torch.dist(a,b,p=1)) #a与b之间的1范数
print(torch.dist(a,b,p=2)) #a与b之间的2范数(欧氏距离)
print(torch.dist(a,b,p=3))
print(torch.norm(a))
print(torch.norm(a,p=1)) #a的1范数
print(torch.norm(a,p='fro'))#a的核范数
(2).tensor中的矩阵分解
常见的矩阵分解
- LU分解:将矩阵A分解成L(下三角)矩阵和U(上三角)矩阵的乘积
- QR分解:将原矩阵分解成一个正交矩阵Q和一个上三角矩阵R的乘积
- EVD分解:特征值分解
- SVD分解:奇异值分解
特征值分解:
- 将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法
- 特征值VS特征向量

PCA与特征值分解
PCA:将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
PCA算法的优化目标就是:
- 降维后同一纬度的方差最大
- 不同维度之间的相关性为0
- 协方差矩阵
奇异值分解:A就是奇异值
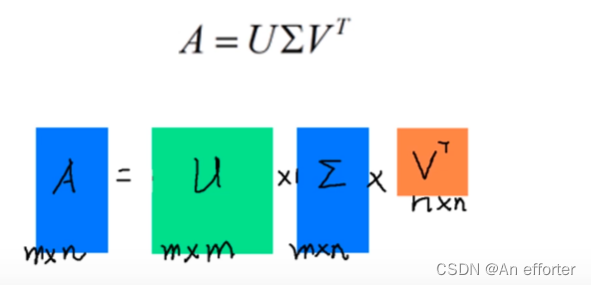
LDA与奇异值分解
找到一条线,能够使得同类的样本之间的距离尽可能小,而不同类的样本尽可能大。
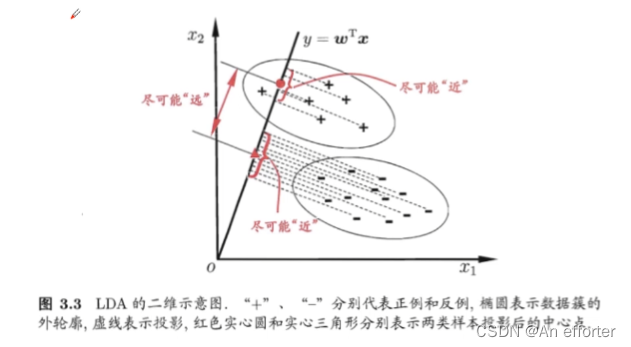
EVD分解VS SVD分解
- 矩阵方阵且满秩(可对角化)
- 矩阵分解不等于特征降维度
- 协方差矩阵描述方差和相关性
Pytorch中的奇异值分解
- torch.svd()
5.Pytorch与张量的操作(裁剪、索引与数据筛选,组合与拼接、切片、变形、填充)
裁剪
(1).pytorch与张量的裁剪
- 对Tensor中的元素进行范围过滤(1.将数据约束到小的范围中,我们的网络在训练的时候就会相对稳定,能够防止过拟合。2.loss值趋于稳定,达到最优解。3.通过对tensor的定点化/量化。)
- 常用于梯度裁剪(gradient clipping),即在发生梯度离散或者梯度爆炸时对梯度的处理
- a.clamp(2,10)
clamp()函数让参数保持到2,5之间,约束参数自己调。如果说小2,约束之后是2,如果说大于5,那么约束为5.
import torch
a=torch.rand(2,2)*10
print(a)
a=a.clamp(2,5)
print(a)
(2).Pytorch与张量的索引与数据筛选
- torch.where(condition, x, y)︰按照条件从x和y中选出满足条件的元素组成新的tensor;
- torch.gather(input, dim, index, out=None):在指定维度上按照索引赋值输出tensor;
- torch.index_select(input, dim, index, out=None):按照指定索引输出tensor;
- torch.masked_select(input, mask, out=None):按照mask输出tensor,输出为向量;
- torch.take(input, indices):将输入看成1D-tensor,按照索引得到输出tensor;
- torch.nonzero(input, out=None):输出非O元素的坐标。
torch.where(): 如果是大于0.5讲选择a,反之选择b。
a= torch. rand ( 2,2)
b = torch.rand (2,2)
print(a)
print(b)
out = torch . where(a > 0.5,a,b) #如果是大于0.5讲选择a,反之选择b
print(out)
torch.index_select(input, dim, index, out=None):按照指定索引输出tensor;
a= torch. rand (4,4)
print(a)
out=torch.index_select(a,dim=0,index=torch.tensor([0,3,2]))
print(out)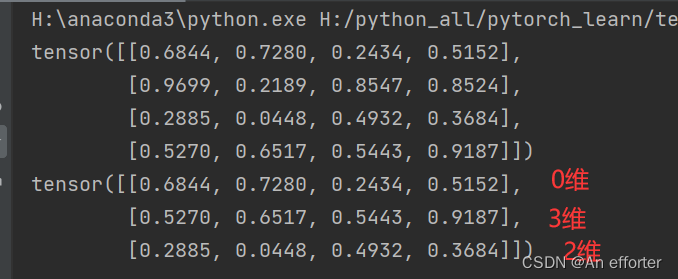
torch.gather(input, dim, index, out=None):在指定维度上按照索引赋值输出tensor;
a = torch .linspace ( 1,16 ,16).view( 4,4)
print(a)
out=torch.gather(a,dim=0,index=torch.tensor([[0,1,1,1],
[0,1,2,2],
[0,1,3,3]]))
print(out)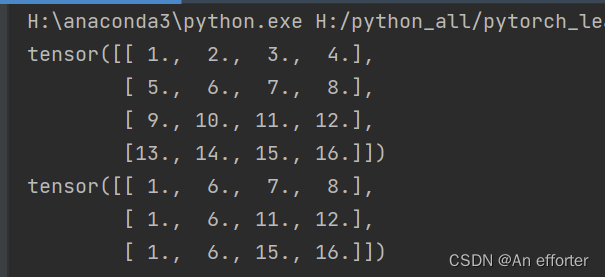
torch.masked_select(input, mask, out=None)
a = torch .linspace ( 1,16 ,16).view( 4,4)
mask=torch.gt(a,8) #a>8为 true
print(out)
print(mask)
out=torch.masked_select(a,mask)
print(out)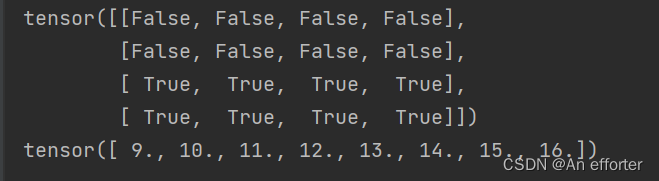
torch.take()根据索引找出值
a = torch .linspace ( 1,16 ,16).view( 4,4)
print(a)
b=torch.take(a,index=torch.tensor([0,15,13,10]))
print(b)torch.nonzero(a) 非零元素的找出坐标
a = torch. tensor([[0,1,2,0],[2,3,0,1]])
print(a)
out = torch. nonzero(a) #打印的是非0元素的坐标
print (out)