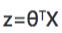一、线性回归:
1.概念:线性回归就是对原数据进行一系列数据拟合,并尽可能构造一条可以拟合数据的数学模型,根据这个模型,输入测试数据进而预测数据的结果
例如:房价问题, 通过房屋面积、卧室多少等绘制一条散点图,通过运算拟合出一条数据模型,通过数据模型,输入房屋面积与卧室数量等信息预测房价。

2.线性回归假设函数:theta:权重参数,x:输入特征的参数

矢量化:

3.线性回归的损失函数:

4.线性回归的优化:使用梯度下降法使损失函数降为最小(对J(theta)进行求导)

进行多次for循环,更新theta权重,进而算是函数也在不同变化,即损失函数的导数为0, 即损失函数已经降到最低,即误差最小

注意:学习率alpha不能太小,不能太大,否则不能准确找到损失函数的最小值
二、逻辑回归(分类回归):
1.概念:通过一系列数据建立一条拟合数据的模型,来预测未来某一数据的走向,逻辑回归则是建立模型将数据分为不同的类别,并预测某个数据的类别

2.逻辑回归假设函数:逻辑回归的假设函数不能使用线性回归的那样的线性函数作为假设函数,因为像散点式数据集也很难通过线性函数模拟,这里我们通过sigmoid函数来作为假设函数

3.为什么我们要采用这一S型函数呢?
当h>=0.5时,预测为1
当h<0.5时,预测为0

我们不能准确的预测y值,但是我们通过这里y值,例如y=0.7,则可以最大化估计1
4.逻辑回归假设函数为:

5.逻辑回归损失函数:
真正代价函数: ![]()
上图公式,只是针对一个样本数据,我们要对整个数据集进行运算,公式如下:

6.对逻辑函数的优化:对损失函数进行求偏导,得到:

三、区别:
1.线性回归要求因变量是连续性数值变量,而logistic回归要求因变量是分类型变量。
2.线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
3.线性回归是直接分析因变量与自变量的关系,而logistic回归是分析因变量取某个值的概率与自变量的关系
四、联系:
1.假设函数不同
一个使线性计算公式, 一个使sigmoid函数计算公式
2.性质不同