前言
很多学习C语言之后就会对各种类型感到很烦,但是数据的类型具有相当的意义。首先是类型决定了大小,即该数据在内存中开辟的空间大小;同时不同的类型还决定了数据存储的方式,相同的数据,存入整形与浮点型方式就不相同。
目录
大小端模式
大端模式:是指数据的高字节保存在内存的低地址中,而数据的低字节保存在内存的高地址中,这样的存储模式有点儿类似于把数据当作字符串顺序处理:地址由小向大增加,数据从高位往低位放;
小端模式:是指数据的高字节保存在内存的高地址中,而数据的低字节保存在内存的低地址中,这种存储模式将地址的高低和数据位权有效地结合起来,高地址部分权值高,低地址部分权值低。
如图,整形1的十六进制序列位0x 00 00 00 01,在内存中低字节部分01存在在较低的地址,也就是小端储存,决定哪种储存方式是由计算机的硬件决定的。
#include<stdio.h>
#include<limits.h>
int main()
{
int num_1 = 1;
if (*(char*)&num_1 == 1)
printf("小端储存");
else
printf("大端储存");
return 0;
}
整形
我们以int类型为例子讲解,首先我们知道int是4个字节,而一字节是八比特,因此有符号的int类型总共是三十二个比特位。
最高位是符号位,也就是决定正负位置,0为正,1为负数。之后剩下的三十一位则用来表示数据的大小,从二的零次方开始,一直到二的三十次方,当三十一位都是1的时候表示最大的数字,也就是二的三十一次方减一,也就是程序员最经典的数字2147483647。
而整形在内存中存储的方式则是以补码的形式存在,对于一个给定的整数,我们可以写成二进制的形式,这就是原码,对每一位按位取反,即0变成1,1变成0,这样就得到了反码,然后反码加一就得到了补码,然后储存在内存中的整形都是以补码的形式存在的,下面举出例子让大家看看。
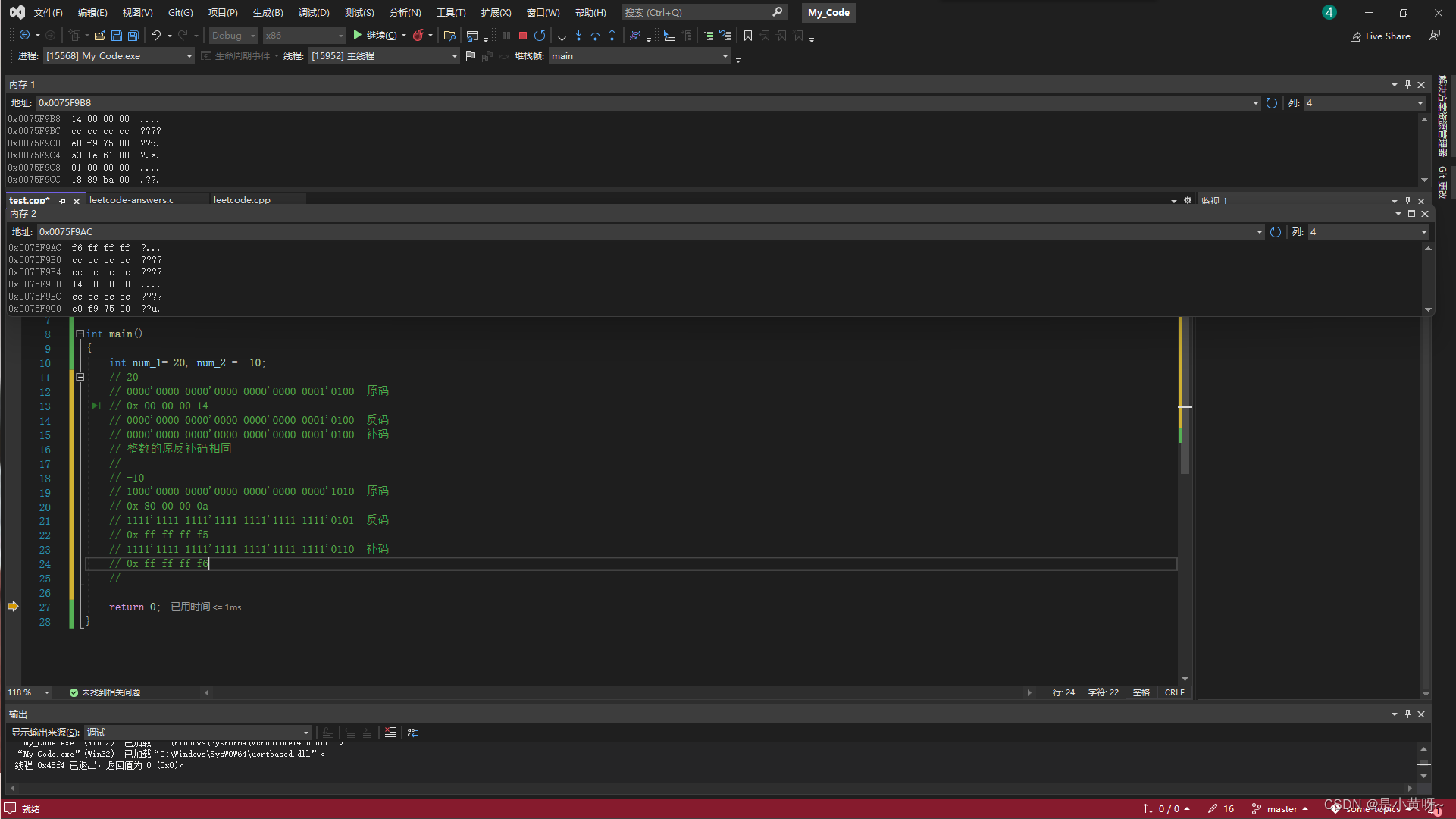
下面定义了两个变量num_1, num_2,由于内存显示是十六进制的方式,所以同时也给出十六进制的表示形式,下图中内存1是num_1的地址,内存2是num_2的地址,可以看到在内存中储存的是补码。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int main()
{
int num_1= 20, num_2 = -10;
// 20
// 0000'0000 0000'0000 0000'0000 0001'0100 原码
// 0x 00 00 00 14
// 0000'0000 0000'0000 0000'0000 0001'0100 反码
// 0000'0000 0000'0000 0000'0000 0001'0100 补码
// 正整数的原反补码相同
//
// -10
// 1000'0000 0000'0000 0000'0000 0000'1010 原码
// 0x 80 00 00 0a
// 1111'1111 1111'1111 1111'1111 1111'0101 反码
// 0x ff ff ff f5
// 1111'1111 1111'1111 1111'1111 1111'0110 补码
// 0x ff ff ff f6
return 0;
}
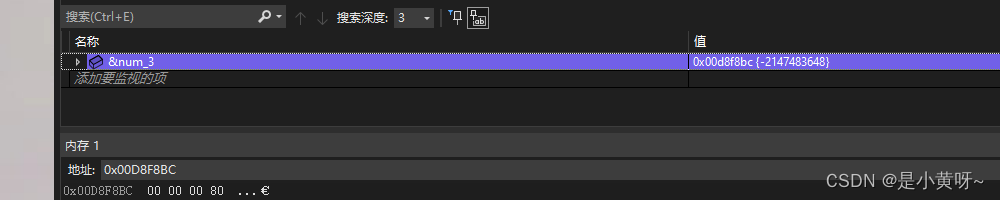
如果后三十一位全部是一是最大的话,似乎也就是最大2147483647的数字了,但是实际上int类型最小值是-2147483648,而这种情况就对于符号位1,其余全部是0,如下图。
而之所以用补码进行存储,原因在于补码可以将符号位和数值位,加法和减法统一处理,而cpu只有加法器也就是只能进行加法,同时由补码变回原码的过程和原码得到补码的过程是相同的,不需要额外的硬件电路。
举例来说1-1,可以视作1+(-1),具体的可以看下面的解释过程,而由补码得到原码的过程,大家可以自行尝试一下,先按位取反,在+1即可。
#include<stdio.h>
#include<limits.h>
int main()
{
int num_1 = 1, num_2 = -1;
// 1
// 0000'0000 0000'0000 0000'0000 0000'0001 原码/反码/补码
//
// -1
// 1000'0000 0000'0000 0000'0000 0000'0001 原码
// 1111'1111 1111'1111 1111'1111 1111'1110 反码
// 1111'1111 1111'1111 1111'1111 1111'1111 补码
//
// 若原码计算则1+(-1)得到
// 1000'0000 0000'0000 0000'0000 0000'0010 结果是-2 很明显不对
// 若补码计算则得到
// 1 0000'00000 0000'00000 0000'00000 0000'00000 然而int类型只能存储三十二位,因此会舍去多出的一位1
// 即保存的是 0000'00000 0000'00000 0000'00000 0000'00000,也就是 0
return 0;
}浮点型
一个浮点数 (Value) 的表示其实可以这样表示:
也就是浮点数的实际值,等于符号位(sign bit)乘以指数偏移值(exponent bias)再乘以分数值(fraction)。我们分别用SEM来表示S符号位,E指数偏移值,M分数值。
而由于E可能出现负数的情况,因此E会加上一个中间值,对于float中间值是127,double则是1023,具体举例可以自行尝试0.5,对应的SEM就是0,-1,0.1。同时由于科学表示法首位必定是1,所以储存中M的第一位不用存储。
下面通过几个例子给大家讲解:
#include<stdio.h>
#include<limits.h>
int main()
{
float num_1 = 5.0, num_2 = 9.5, num_3 = 9.6;
//s
// 5.0
// 101.0 二进制序列
// 1.01 * 2^2 科学表示法
// 5.0 = (-1)^0 * 1.01 * 2^2 对应SEM
// S = 0, E = 2, M = 1.01 ,E存储中加上了一个中间值 因此存入为129
// 即内存中储存的为
// S E M
// 0 10000001 01000000000000000000000
// 0100 0000 1010 0000 0000 0000 0000 0000
// 0x 40 a0 00 00
//
// 9.5
// 1001.1 二进制序列,其中小数点后第一位表示2^(-1)
// 9.5 = (-1)^0 * 1.0011 * 2^3 对应SEM
// S = 0, E = 3, M = 1.0011
// 即内存中储存的为
// S E M
// 0 10000010 00110000000000000000000
// 0100 0001 0001 1000 0000 0000 0000 0000
// 0X 41 18 00 00
//
// 9.6
// 1001.1001… 科学表示法无法表示完全,也就造成了所谓的精度丢失问题
return 0;
}
最后对于浮点数读取有两个特殊情况,即E为全0或者全1,对应表示为2^(-127)和2^128,表示一个无穷接近于正负0和无穷正负大的数字。