本文是在GPU版本的Tensorflow = 2.6.2 , 英伟达显卡驱动CUDA版本 =11.6,Python版本 = 3.6, 显卡为3060的环境下进行验证实验的!!!
文章目录
一、M-P神经元模型
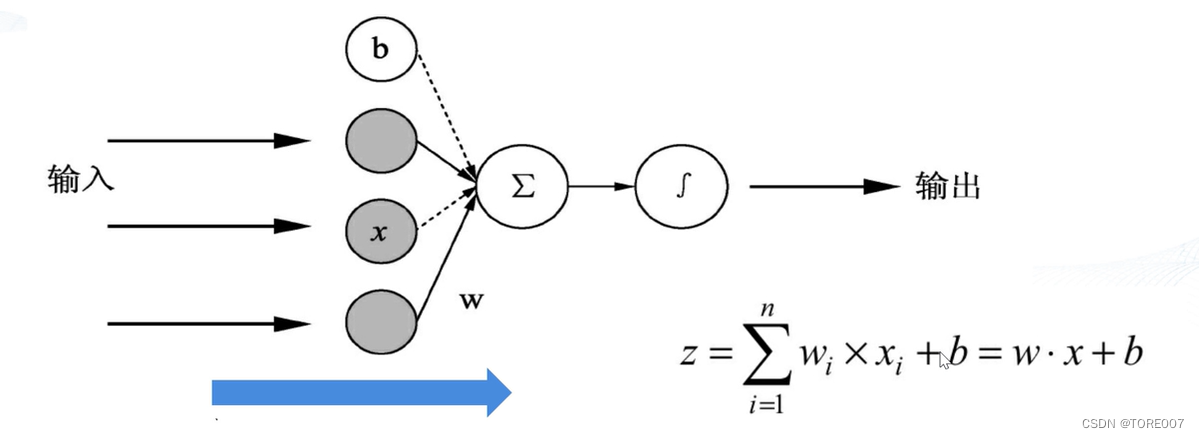
- 每个神经元都是由多个输入单输出的信息处理的单元,由于每个输入所起的贡献程度不同,因此需要将每个输入乘以权重值进行求和,再加上一个偏置项构成某个神经元的输入,经过激活函数后即可得到该神经元的输出
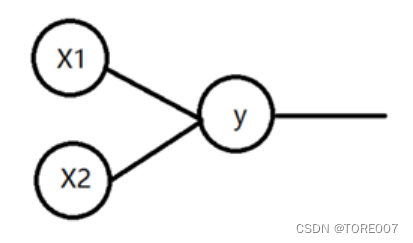
- 训练单个神经元实例说明
一个含有两个输入的神经元,指定一个输入x1=x2=1,期望y能输出0.3。要求不断的输入x1=x2=1,然后不断的训练权重w与偏置b值,训练一万次后,再次输入x1与x2输出y的值是否为0.3?
部分代码详解:
- tf.truncated_normal()函数用来产生符合正态分布的变量,tensorflow提供的三种变量初始化正态分布的某种形状见Tensorflow深度学习实战之(三)–变量的定义以及初始化
- tf.nn.sigmoid(x, name=None)函数常被用做神经网络的激活函数,将变量映射到0,1之间,参数X是一个张量
import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()
x = tf.constant([[1.0,1.0]]) #创建大小为(1,2)的矩阵数组作为输入
w = tf.Variable(tf.truncated_normal([2,1]), name='weights') #w是图中权重的变量是一个2行1列的矩阵。矩阵的初值为符合正太分布随机值的变量,类型保持一致
b = tf.Variable(tf.truncated_normal([1]), name='bias') #b计算偏置值,初值为的符合正太分布随机值的变量
y = tf.nn.sigmoid(tf.matmul(x,w)+b) #两个矩阵相乘其类型要一致,将加权值加上偏置值传入sigmod激活函数使其结果再0-1范围
y1 = tf.placeholder(tf.float32) #实际的y值,此处仅定义占位。在运算过程中进行赋值
cost = tf.reduce_sum(tf.square(y1-y)) #建立损失函数
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost) #使用阶梯下降算法进行优化损失函数使其找到使其达到最小值时对应的w、b参数值
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
for line in range(10000):
sess.run(train_step, feed_dict={y1:0.3}) #将y1数据喂入到模型进行训练
print("line:",line,"w:",sess.run(w),"b",sess.run(b))
print(sess.run(y))
最后运行出的结果为:
[[0.30000356]]
二、BP神经网络模型
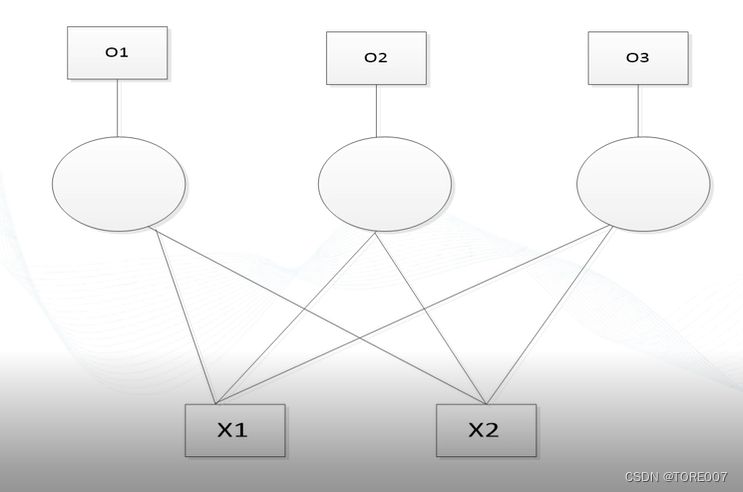
1. 感知机模型
即单层神经网络,是最基础的神经网络模型结构,参与计算的神经元有一个或多个,每个神经元有一个或多个输入,同时产生一个或多个输出模型。
2. BP神经网络模型
在感知机模型上进行扩展演化成即误差反向传播算法(Error Back Propagation Training),主要解决多层神经网络隐含层连接权学习问题,模型包含输入层、一个或多个隐含层和输入层三个部分组成,每个节点与上一层的所有节点都有连接即全连接,网络的输出层由一个或多个输出节点组成,输出节点个数由分类类别数决定。
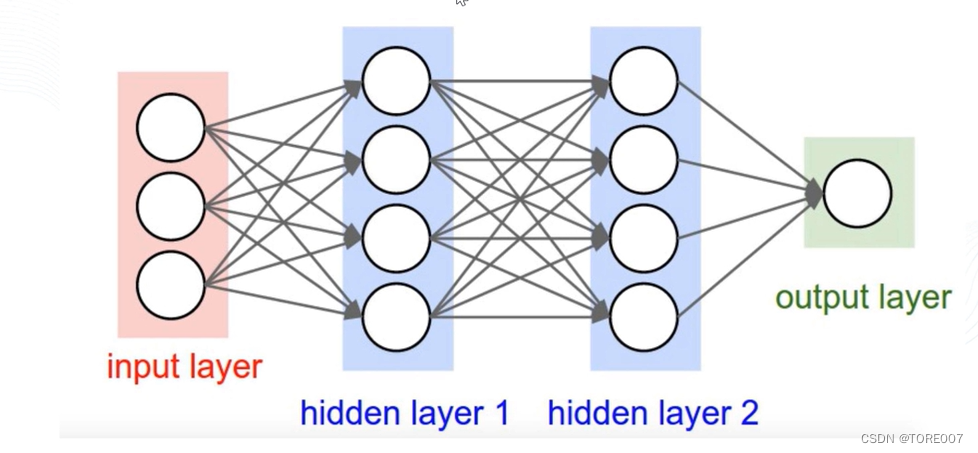
3.BP神经网络传播过程
- 第一阶段:信号的前向传播,从输入层经过隐含层,最后到达输出层
- 第二阶段:误差的反向传播,从输出层到隐含层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置,因为一开始权重和偏置时随机分配的,正向传播生成的结果与实际结果有误差,需要反向传播将误差传递给权重和偏置让其进行调整成合适的值。
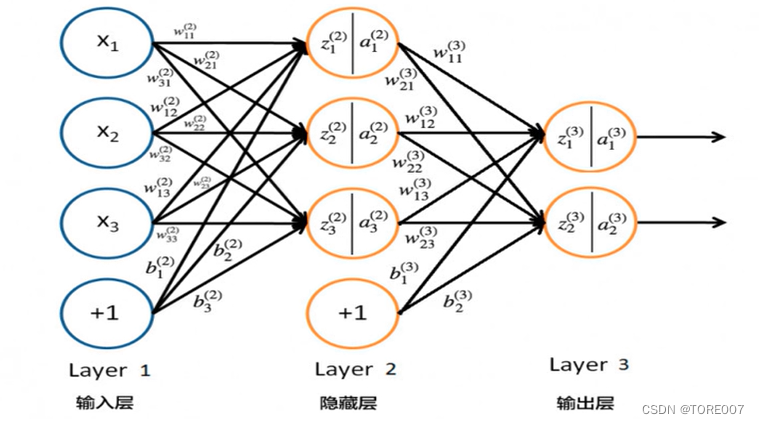
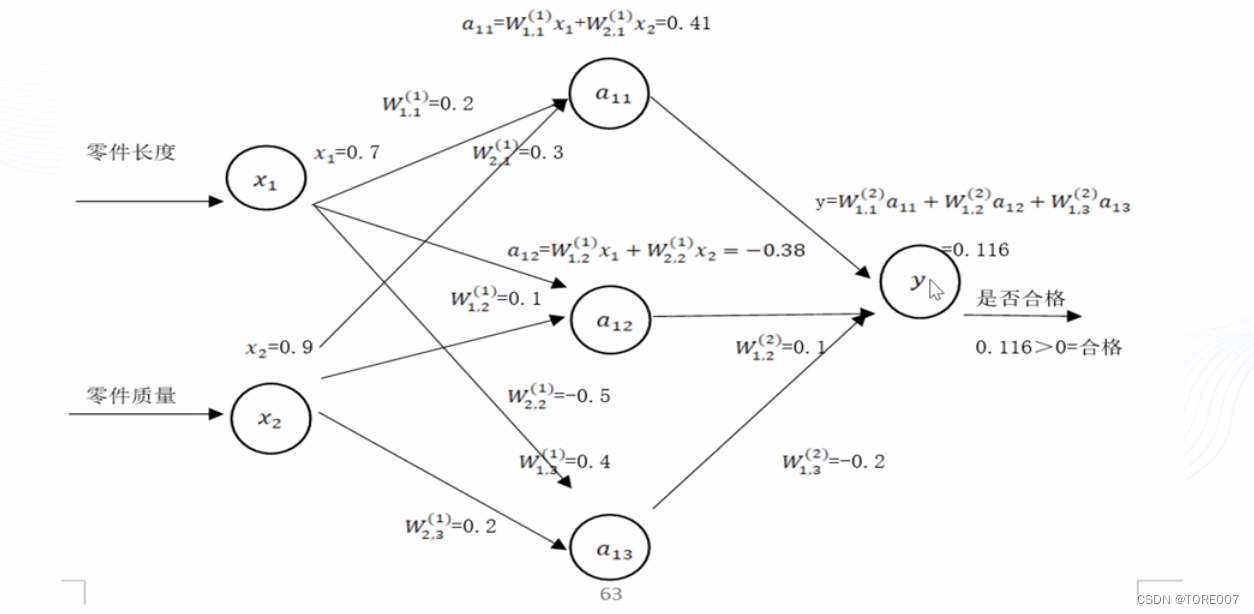
4. BP神经网络向前推导
神经网络向前传播过程需要三部分信息:
- 神经网络的输入,这个输入就是从实体中提取的特征向量,有几个特征输入层就有几个节点数构成特征向量;
- 神经网络的连接结构,它给出不同神经元之间输入和输出的连接关系,隐藏层的节点数根据应用领域的实际问题而确定,找到最优的隐藏层的节点数;
- 最后一部分给出了神经元的参数,即对应的权重和偏置项的参数
如有一个判断零件是否合格的神经网络模型,输入零件的长度和质量,从而检测文件是否合格,如图所示
import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()
x = tf.constant([[0.7,0.9]])
w1 = tf.Variable(tf.random_normal([2,3],stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1, seed=1))
y1 = tf.matmul(x,w1)
y2 = tf.matmul(y1,w2)
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
print(sess.run(y2))
程序运行结果为:
[[3.9582856]]
5.BP神经网络训练过程
- 定义神经网络前向传播的结构、各个参数以及输出结果
- 定义损失函数以及选择反向传播优化的算法
- 生成会话并且在训练数据上反复进行反向传播优化算法
步骤一:定义神经网络前向传播的结构、各个参数以及输出结果
import tensorflow.compat.v1 as tf
tf.compat.v1.disable_eager_execution()
from numpy.random import RandomState
x = tf.placeholder(tf.float32) #用占位符定义输入参数
w1 = tf.Variable(tf.random_normal([2,3]), stddev=1, seed=1) #定义输入层到隐含层传播的权重
w2 = tf.Variable(tf.random_normal([3,1]), stddev=1, seed=1) #定义隐含层到输出层传播的权重
y1 = tf.matmul(x, w1)
y2 = tf.matmul(w2, y1) #定义的神经网络前向传播结构
y = tf.placeholder(tf.float32) #用占位符定义其输出结果
步骤二:定义损失函数以及选择反向传播优化的算法
loss = tf.reduce_mean(tf.square(y-y2)) #定义损失函数均方差
train_step = tf.train.AdamOptimizer(0.01).minimize(loss) #使用Adma优化器实现反向传播算法最小化损失函数
步骤三:生成会话并且在训练数据上反复进行反向传播优化算法
以下代码进行详细说明如下手稿推导过程:
X = rdm.rand(dataset_size, 2)
Y = [[int(x1 + x2 < 1)] for (x1, x2) in X]
for i in range(5000):
start = (i * batch_size) % dataset_size
end = min(start + batch_size, dataset_size)
#随机生成数据集,并自定义标签,生成的输入X维度为(128,2),标签Y的维度为(128,1),可以认为输入为产品两个属性值x1和x2,如果x1+x2<1则被认为是合格产品,标签为Y为1,否则标签Y为0
rdm = RandomState(1)
batch_size = 8
dataset_size = 128 #共设置128组数据
X = rdm.rand(dataset_size, 2)
Y = [[int(x1 + x2 < 1)] for (x1, x2) in X] #对X中的每一组元素(x1, x2)遍历一遍,当满足(x1+x2<1)时,就把这个布尔值[True]/[False]转换成int型(1或0),存放在[]里,作为Y的一个元素。
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op)
print("训练之前的初始权重w1:",sess.run(w1))
print("训练之前的初始权重w2:",sess.run(w2))
for i in range(5000):
start = (i * batch_size) % dataset_size
end = min(start + batch_size, dataset_size)
sess.run(train_step, feed_dict={x:X[start:end],y:Y[start:end]})
if i%1000 == 0:
print("epoch:",i,"loss:",sess.run(loss,feed_dict{x:X[start:end],y:Y[start:end]}))
print("训练之后的权重w1:",sess.run(w1))
print("训练之后的权重w2:",sess.run(w2))
训练之后的结果为:
训练之前的初始权重w1: [[-0.8113182 1.4845989 0.06532937]
[-2.4427042 0.0992484 0.5912243 ]]
训练之前的初始权重w2: [[-0.8113182 ]
[ 1.4845989 ]
[ 0.06532937]]
epoch: 0 loss: 6.248947
epoch: 1000 loss: 0.39603534
epoch: 2000 loss: 0.39598295
epoch: 3000 loss: 0.39611232
epoch: 4000 loss: 0.39599258
训练之后的权重w1: [[-0.18695419 0.79214305 1.1778173 ]
[-2.09508 -0.24159996 0.46650133]]
训练之后的权重w2: [[-0.42987412]
[ 0.75521606]
[-0.5841582 ]]
本文含有隐藏内容,请 开通VIP 后查看