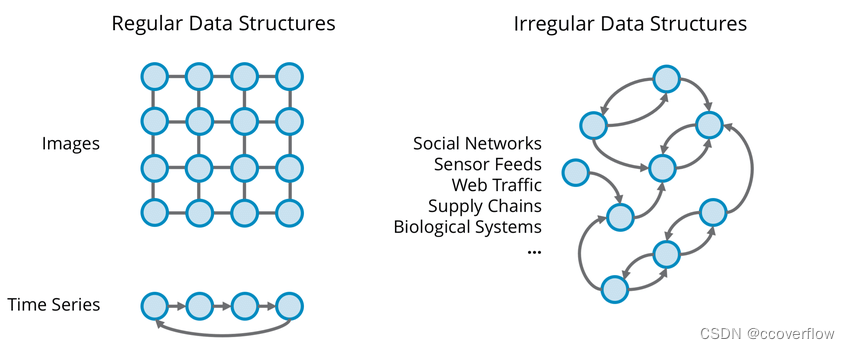
绝大多数深度学习是在 欧几里得数据（Euclidean Data） 上进行的。这包括1维和2维域中的数据类型。但我们并不存在于一维或二维世界。所有我们能观察到的都存在于3D中，我们的数据应该反映出这一点。

图像、文本、音频和许多其他都是欧几里得数据。

非欧几里得数据（Non-euclidean Data） 可以比一维或二维表示更精确地表示更复杂的东西和概念：

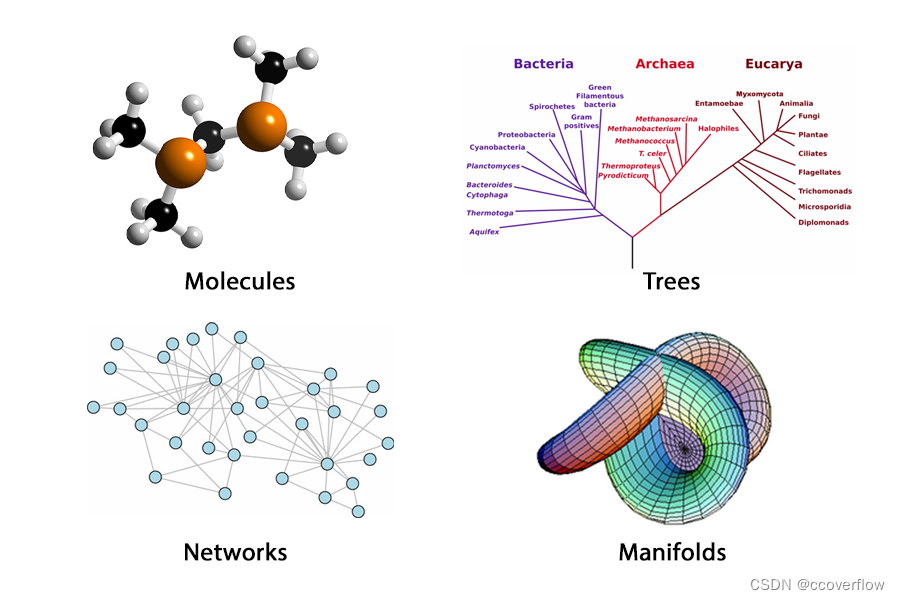
当我们用非欧几里得的方式来表示事物时，我们给了它一种归纳偏置（inductive bias）。这是基于这样一种直觉：给定任意类型、格式和大小的数据，可以通过更改数据的结构来确定模型的优先级，以了解特定的模式。

归纳偏置（英语：Inductive bias 也称为 Learning bias），指的是学习算法中，当学习器去预测其未遇到过的输入结果时，所做的一些假设的集合（Mitchell, 1980）。

机器学习试图去建造一个可以学习的算法，用来预测某个目标的结果。要达到此目的，要给于学习算法一些训练样本，样本说明输入与输出之间的预期关系。然后假设学习器在预测中逼近正确的结果，其中包括在训练中未出现的样本。既然未知状况可以是任意的结果，若没有其它额外的假设，这任务就无法解决。这种关于目标函数的必要假设就称为归纳偏置（Mitchell, 1980; desJardins and Gordon, 1995）。

维基百科：归纳偏置

基于这种直觉，几何深度学习（GDL） 是深度学习中的小众领域，旨在建立可以从非欧氏数据中学习的神经网络。

非欧几里得数据类型的主要例子是图。图是一种由节点（实体）组成的数据结构，这些节点（实体）与边（关系）相连。这个抽象的数据结构几乎可以用来建模任何东西。

我们希望能够从图表中学习，因为:

图能够表示个体的特征，同时提供了关系和结构的信息。

有各种类型的图，每一种都有一组规则、属性和可能的操作。图论是研究图以及我们可以从中学到什么。我们在本系列的下一部分中讨论。

几何深度学习的例子

这是文献中比较流行的两个应用和研究重点。它们经常被用作（非官方的）基准。

分子建模与学习

关于图学习如何改善现有机器学习任务的具体例子。

计算化学、生物学和物理学的瓶颈之一是表示概念、实体和相互作用。科学的本质是经验的，因此是许多外部因素和关系的结果。以下是一些最明显的例子:

• Protein interaction networks 蛋白质相互作用网络
• Neural networks 神经网络
• Molecules 分子
• Feynman diagrams 费曼图
• Cosmological maps 宇宙地图

我们目前通过计算来表示这些概念的方法可以被认为是“有损的”，因为我们会失去很多有价值的连接信息。例如，使用一个simplified-molecular-input-line-entry-system (SMILE) 字符串来表示分子很容易计算，但代价是失去了分子的结构信息。

通过把原子当作节点，把键当作边，我们可以保存结构信息，这些信息可以用于下游的预测或分类。

因此，我们可以使用分子图作为其几何等价的输入，而不是使用一个表示分子的字符串作为递归神经网络（RNN）的输入。

三维建模与学习

这是几何深度学习从未使用过的数据类型中学习的一个例子，考虑一个人对着相机摆姿势：

这个图像是二维的，尽管在我们的脑海中，我们知道它代表了一个三维的人。我们目前的算法，即卷积神经网络(CNN)，非常擅长预测标签，比如只给出2D图像的人的姿势和/或姿势类型。当姿势变得极端，角度不再固定时，困难就出现了。通常情况下，图像中可能会有衣服或物体阻碍算法的视线，这使得预测姿势变得困难。

现在想象一下这个人正在摆姿势的3D模型:

CNN现在可以在3D对象本身而不是对象的2D图像上运行。

与其从数据限制在单个透视角度的 2D 表示中学习，不如想象一下我们是否可以直接在对象本身上运行卷积。 与传统的 CNN 类似，kernel将通过表示为点云（基本上是环绕 3D 对象的图形）中节点的每个“像素”。3D模型上的每个角落和缝隙都将被覆盖，信息将被考虑。 简而言之，普通 CNN 模型与 Geometric 模型之间的区别在于，在给定图片的情况下预测 n 个对象的标签，而不是在给定对象的 3D 模型的情况下预测对象的标签。

随着我们 3D 建模、设计和打印技术的改进，人们可以想象这将如何产生更加准确和精确的结果。

维度（Dimensions）

传统意义上的维度

维度的概念在数据科学和机器学习中已经被广泛使用，其中 “维度”的数量与数据集中特征的数量 / 每个示例的属性数量 / 数据集中的数据点数量 相关。

一开始，机器学习算法的性能会突飞猛进，但经过一定数量的特征(维度)后，性能会趋于稳定。这就是众所周知的 “维度诅咒”。

几何深度学习不能解决这个问题。相反，图卷积这样的算法减少了使用具有大量特性的数据类型时产生的性能损失，因为 关系数据是通过归纳偏差来考虑的，而不是作为一个额外的特性 。

当我们谈论维度时，我们谈论的是什么

几何深度学习中的维数只是一个用于训练神经网络的数据的问题。欧几里得数据服从欧几里得几何规律，而非欧几里得数据服从非欧几里得几何规律。

非欧几里得几何可以用这样一句话来概括：

两点之间的最短路径不一定是直线（the shortest path between 2 points isn’t necessarily a straight line） —StackExchange A.I stream post

还有一些特殊规则包括:

• 三角形的内角和总是大于180度
• 平行线可以无限相交，也可以永不相交
• 四边形可以用曲线作为边

图像是最流行的欧几里得数据类型之一：

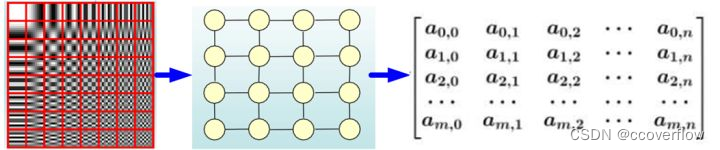
由像素组成的图像具有左、右、上和下的概念。可以通过递归地在图像上转换函数来遍历图像，这正是CNN的原理。

然而，在图上，没有左、右、上或下的概念。只有一个节点连接到任意数量的节点。节点甚至可以连接到自身。

在使用非欧几里得数据训练神经网络时，仍然存在机器和深度学习传统意义上的维度（Dimensions）。 例如，节点有多个特征，其中每个特征都是另一个“维度”。 但该术语在文献中很少使用来表示这一点。

标准 vs 全新的概念

机器学习以深度学习为中心，而深度学习本身围绕着一些流行的算法。 每个算法都粗略地专注于特定的数据类型。 正如 RNN 是为时间相关数据构建的，而 CNN 是为图像类型数据构建的一样，图神经网络 (GNN) 是一种为图和网络构建的几何深度学习算法。 正如 Expero 数据科学主管 Graham Ganssle 所说：

Graph convolutional networks are the best thing since sliced bread because they allow algos to analyze information in its native form rather than requiring an arbitrary representation of that same information in lower dimensional space which destroys the relationship between the data samples thus negating your conclusions. —
Graham Ganssle (in a Tweet)
翻译：Graph convolutional networks是自切片面包以来最好的东西，因为它们允许算法以原始形式分析信息，而不是要求在低维空间中任意表示相同的信息，这会破坏数据样本之间的关系，从而否定你的结论

图卷积网络或GCNs之于图神经网络就像cnn之于 Vanilla neural networks。

这种新方法的含义有很大的不同； 我们不再被迫在数据集中留下重要信息。 诸如结构、关系和连接之类的信息，对于一些最重要的数据提供任务和行业（如交通、社交媒体和蛋白质网络）来说是不可或缺的。

简而言之，几何深度学习领域有 3 个主要贡献：

• 我们可以利用非欧几里得数据
• 我们可以最大限度地利用我们收集的数据中的信息
• 我们可以使用这些数据来教授机器学习算法

在一篇论文中证明了图学习算法可以被推广并模块化以用于各种应用和增强，据说：

We argue for making generalization a top priority for AI, and advocate for embracing integrative approaches which draw on ideas from human cognition, traditional computer science, standard engineering practice, and modern deep learning. — DeepMind, Google Brain, MIT, and the University of Edinburgh
翻译：我们主张将generalization作为人工智能的重中之重，并提倡采用综合方法，这些方法借鉴了人类认知、传统计算机科学、标准工程实践和现代深度学习的思想

换句话说，我们对几何深度学习有很多期待。

回到本质

什么是几何深度学习（Geometric Deep Learning）？

Geometric Deep Learning is a niche in Deep Learning that aims to generalize neural network models to non-Euclidean domains such as graphs and manifolds.

字典中对niche的解释: a comfortable or suitable position in life or employment.

总结

• 欧几里得域和非欧几里得域遵循不同的规则；每个领域中的数据都专注于某些格式（图像、文本与图表、流形）并传达不同数量的信息
• 几何深度学习是一类可以在非欧几里得域上运行的深度学习，目的是教授模型如何对关系数据类型进行预测和分类
• 传统深度学习和几何深度学习之间的区别可以通过想象扫描人的图像与扫描人本身的表面之间的准确性来说明。
• 在传统的深度学习中，维度与数据中的特征数量直接相关，而在几何深度学习中，它指的是数据本身的类型，而不是它具有的特征数量。

自2019年以来，这个领域已经发生了很大的变化。

几何深度学习现在被用于Pinterest、Twitter、Uber、埃森哲等公司的前沿，而且这个列表还涵盖了几乎每一家涉足ML领域的公司。在学术界，从NeurIPS到ICML，图表示学习和相关术语不断成为会议讨论的主题。我们开始看到跨领域的比较和具有新颖应用的新颖模型。

仅仅几年的时间，对GDL进行总结就已经很困难了，所以学无止境啊…