天鹰优化算法(Aquila Optimizer)是一种元启发式优化算法发表在中科院SCI一区期刊(Computers & Industrial Engineering)上的文章:“Aquila Optimizer: A novel meta-heuristic optimization algorithm”

01.引言
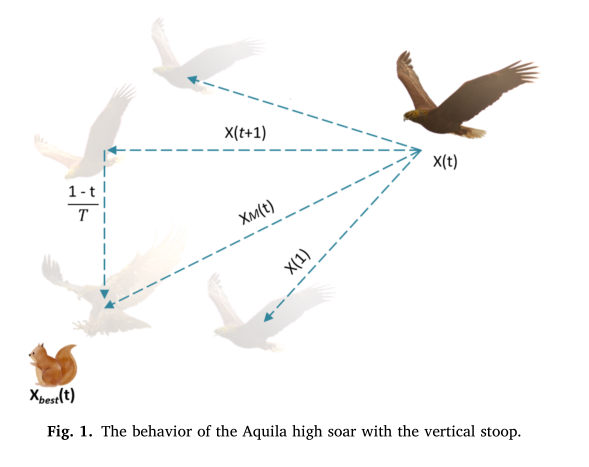
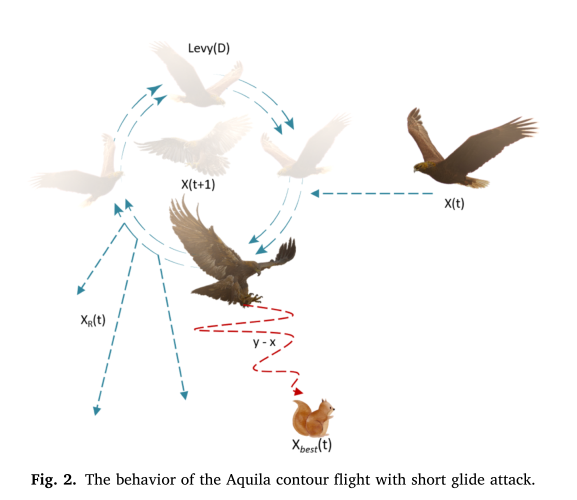
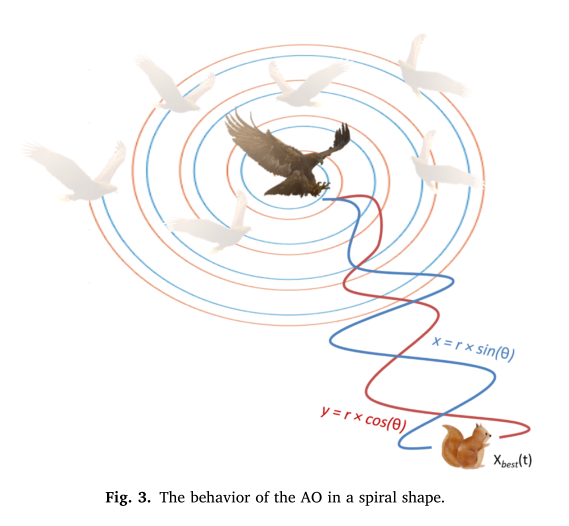
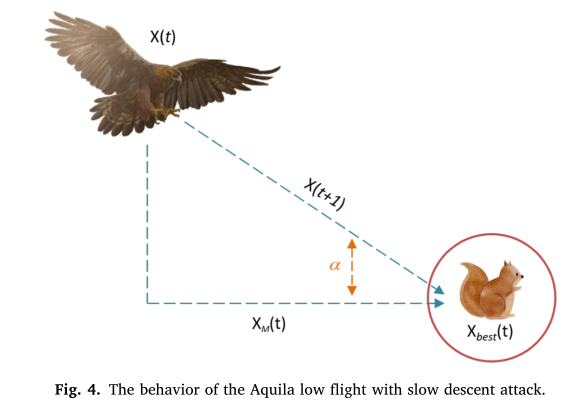
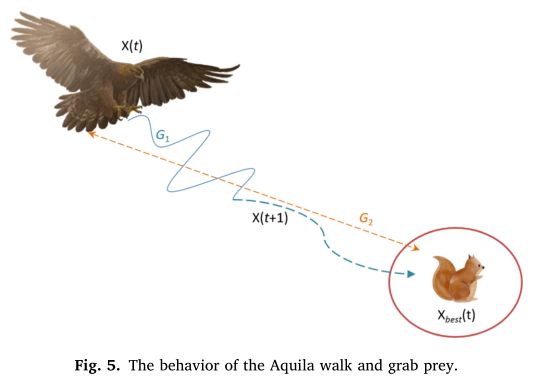
本文从自然界中Aquila捕食过程中的行为出发,提出了一种基于种群的优化方法——Aquila Optimizer (AO)。因此,本文提出的AO算法的优化过程分为四种方法;在发散搜索空间内,采用等高线飞行,采用短降攻击进行搜索;在收敛搜索空间内,采用低飞,采用慢降攻击进行搜索;为了验证新优化器对不同优化问题的寻优能力,进行了一系列的实验。例如,在第一个实验中,AO被应用于寻找众所周知的23个函数的解。第二个和第三个实验系列旨在评估AO的性能,以寻找更复杂问题的解决方案,例如分别使用30个CEC2017测试函数和10个CEC2019测试函数。最后,使用了一组七个实际工程问题。实验结果表明,该算法与常用的元启发式算法相比具有一定的优越性。
02.代码流程图

03.部分代码
%_______________________________________________________________________________________%
% Aquila Optimizer (AO) source codes (version 1.0) %
% %
% Developed in MATLAB R2015a (7.13) %
% Author and programmer: %
% Abualigah, L, Yousri, D, Abd Elaziz, M, Ewees, A, Al-qaness, M, Gandomi, A. %
% e-Mail: Aligah.2020@gmail.com (Laith Abualigah) %
% Homepage: %
% 1- https://scholar.google.com/citations?user=39g8fyoAAAAJ&hl=en %
% 2- https://www.researchgate.net/profile/Laith_Abualigah %
% %
% Main paper: %
%_____________Aquila Optimizer: A novel meta-heuristic optimization algorithm___________%
%_______________________________________________________________________________________%
% Abualigah, L, Yousri, D, Abd Elaziz, M, Ewees, A, Al-qaness, M, Gandomi, A. (2021).
% Aquila Optimizer: A novel meta-heuristic optimization algorithm.
% Computers & Industrial Engineering.
%_______________________________________________________________________________________%
function [Best_FF,Best_P,conv]=AO(N,T,LB,UB,Dim,F_obj)
Best_P=zeros(1,Dim);
Best_FF=inf;
X=initialization(N,Dim,UB,LB);
Xnew=X;
Ffun=zeros(1,size(X,1));
Ffun_new=zeros(1,size(Xnew,1));
t=1;
alpha=0.1;
delta=0.1;
while t<T+1
for i=1:size(X,1)
F_UB=X(i,:)>UB;
F_LB=X(i,:)<LB;
X(i,:)=(X(i,:).*(~(F_UB+F_LB)))+UB.*F_UB+LB.*F_LB;
Ffun(1,i)=F_obj(X(i,:));
if Ffun(1,i)<Best_FF
Best_FF=Ffun(1,i);
Best_P=X(i,:);
end
end
G2=2*rand()-1; % Eq. (16)
G1=2*(1-(t/T)); % Eq. (17)
to = 1:Dim;
u = .0265;
r0 = 10;
r = r0 +u*to;
omega = .005;
phi0 = 3*pi/2;
phi = -omega*to+phi0;
x = r .* sin(phi); % Eq. (9)
y = r .* cos(phi); % Eq. (10)
QF=t^((2*rand()-1)/(1-T)^2); % Eq. (15)
%-------------------------------------------------------------------------------------
for i=1:size(X,1)
%-------------------------------------------------------------------------------------
if t<=(2/3)*T
if rand <0.5
Xnew(i,:)=Best_P(1,:)*(1-t/T)+(mean(X(i,:))-Best_P(1,:))*rand(); % Eq. (3) and Eq. (4)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
else
%-------------------------------------------------------------------------------------
Xnew(i,:)=Best_P(1,:).*Levy(Dim)+X((floor(N*rand()+1)),:)+(y-x)*rand; % Eq. (5)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
end
%-------------------------------------------------------------------------------------
else
if rand<0.5
Xnew(i,:)=(Best_P(1,:)-mean(X))*alpha-rand+((UB-LB)*rand+LB)*delta; % Eq. (13)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
else
%-------------------------------------------------------------------------------------
Xnew(i,:)=QF*Best_P(1,:)-(G2*X(i,:)*rand)-G1.*Levy(Dim)+rand*G2; % Eq. (14)
Ffun_new(1,i)=F_obj(Xnew(i,:));
if Ffun_new(1,i)<Ffun(1,i)
X(i,:)=Xnew(i,:);
Ffun(1,i)=Ffun_new(1,i);
end
end
end
end
%-------------------------------------------------------------------------------------
if mod(t,100)==0
display(['At iteration ', num2str(t), ' the best solution fitness is ', num2str(Best_FF)]);
end
conv(t)=Best_FF;
t=t+1;
end
end
function o=Levy(d)
beta=1.5;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
o=step;
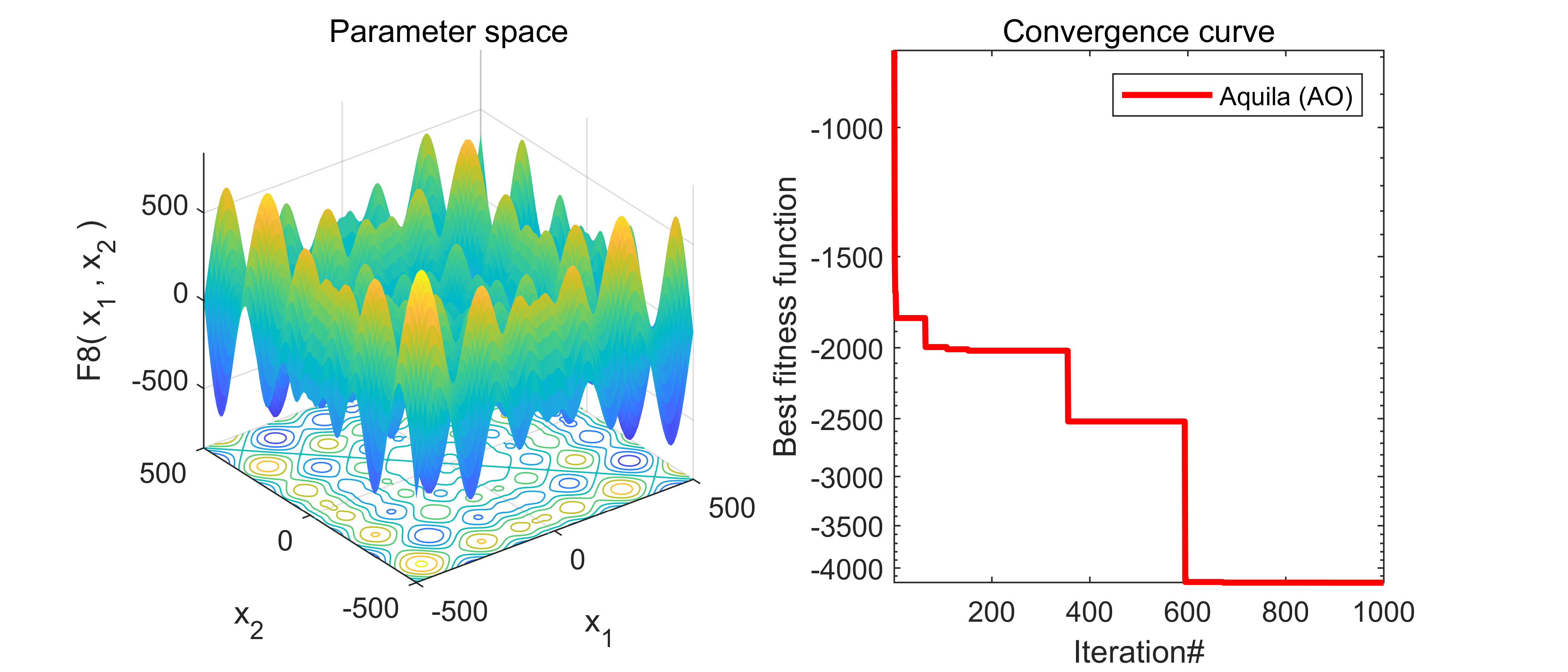
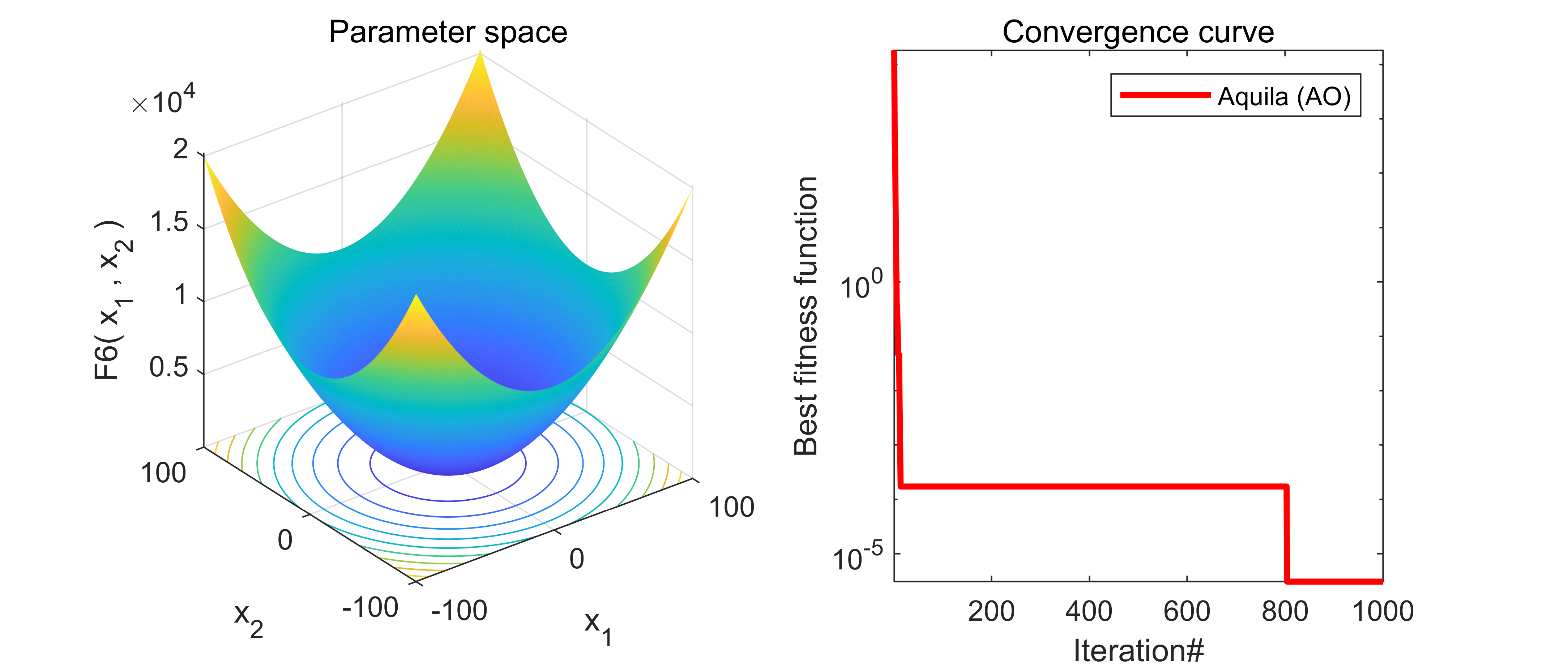
end04.代码效果图
获取代码请关注MATLAB科研小白的个人公众号(即文章下方二维码),并回复:智能优化算法本公众号致力于解决找代码难,写代码怵。各位有什么急需的代码,欢迎后台留言~不定时更新科研技巧类推文,可以一起探讨科研,写作,文献,代码等诸多学术问题,我们一起进步。