顺序统计树在红黑树基础上的扩展与应用：OS-SELECT过程详解-EW帮帮网

一、背景

在计算机科学领域，数据结构和算法是构建高效软件系统的基础。红黑树作为一种高效的自平衡二叉查找树，广泛应用于各种场景，如内存管理、数据库索引和调度算法等。红黑树之所以受到青睐，是因为它能够在最坏情况下保证对数据的查找、插入和删除操作都保持对数复杂度，这对于处理大量数据的系统来说是至关重要的。

然而，红黑树的标准定义并不包括对顺序统计问题的直接支持。顺序统计问题涉及到快速确定集合中第k小的元素或计算元素的排名，这类问题在统计分析、数据挖掘和机器学习等领域中非常常见。为了解决这类问题，研究者们提出了顺序统计树这一概念，它在红黑树的基础上增加了额外的size属性，使得我们可以在O(log n)的时间内回答顺序统计查询。

本文的背景建立在这样的需求之上：我们希望在保持红黑树所有优秀特性的同时，扩展其功能以支持顺序统计操作。为此，我们将深入探讨顺序统计树的原理和实现，并通过具体的示例来阐释如何使用OS-SELECT过程在顺序统计树中查找具有特定排名的元素。此外，我们还将展示如何将OS-SELECT过程从递归形式转换为非递归形式，以适应不同的应用场景和避免潜在的栈溢出问题。

通过本文的阅读，读者将能够理解顺序统计树的设计哲学，掌握OS-SELECT过程的工作原理，并学会如何实现和使用这一过程来解决实际问题。我们将通过丰富的示例和清晰的解释，使读者对这一高级数据结构有一个全面的认识，并能够在自己的项目中有效地应用它。
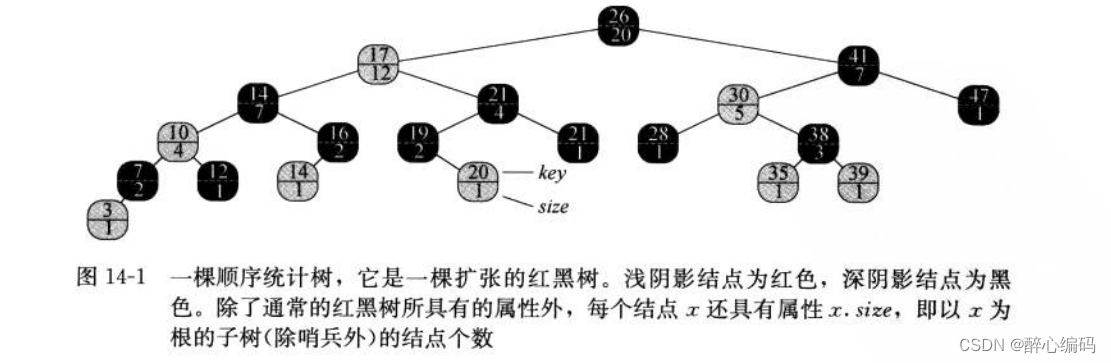
在深入探讨图14-1中的红黑树T执行OS-SELECT(T.root,10)的过程以及编写OS-SELECT的非递归版本之前，让我们首先对红黑树和顺序统计树的概念有一个清晰的认识。
在这里插入图片描述

二、红黑树基础

红黑树是一种自平衡的二叉查找树，它在计算机科学中被广泛应用于数据结构和算法设计中。一棵红黑树具有以下特性：

每个节点要么是红色，要么是黑色。
根节点和叶子节点（NIL节点）都是黑色。
每个红色节点的两个子节点都是黑色（也就是说，红色节点不能连续）。
对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

红黑树的这些特性确保了最坏情况下的查找、插入和删除操作的时间复杂度为O(log n)，其中n是树中节点的数量。

三、顺序统计树

顺序统计树是一种特殊的红黑树，它在每个节点上存储了额外的属性size。这个属性表示以该节点为根的子树中的节点数量（包括节点本身）。利用size属性，顺序统计树可以快速地回答关于动态集合中元素的顺序统计查询，例如找到第k小的元素或计算元素在集合中的排名。

四、OS-SELECT过程

OS-SELECT是顺序统计树中用于查找具有特定排名的元素的过程。给定一个红黑树T和一个整数i，OS-SELECT(T.root, i)将返回树T中排名为i的元素。排名是指元素在树的中序遍历中的顺序位置。

现在，让我们通过图14-1中的红黑树T来详细说明执行OS-SELECT(T.root, 10)的过程：

从根节点开始，计算当前节点x的排名r，r = x.left.size + 1。
如果i等于r，那么当前节点x就是我们要找的第10名元素，返回x。
如果i小于r，说明第10名元素在x的左子树中，递归调用OS-SELECT(x.left, i)。
如果i大于r，说明第10名元素在x的右子树中，递归调用OS-SELECT(x.right, i - r)。

在图14-1中，假设根节点的左子树大小为5，那么根节点的排名为6。因为10小于6，我们知道第10名元素在根节点的左子树中。我们继续在左子树中查找，直到找到排名为10的元素。

五、OS-SELECT的非递归版本

递归版本的OS-SELECT易于理解和实现，但在某些情况下可能会导致栈溢出。因此，非递归版本可以是一个更好的选择。以下是OS-SELECT的非递归版本的伪代码实现：

function OS-SELECT-ITERATIVE(T, i)
  while T ≠ NIL
    if i == 1
      return T
    if i <= T.left.size + 1
      T = T.left
    else
      i = i - (T.left.size + 1)
      T = T.right
  return NIL // 如果没有找到排名为i的元素

在这个非递归版本中，我们使用一个循环来遍历红黑树。我们检查当前节点的左子树大小和排名，然后根据这些信息决定是向左还是向右移动。如果当前节点的排名等于i，我们就找到了目标元素并返回它。如果i小于当前节点的左子树大小加1，我们进入左子树；否则，我们从i中减去左子树的大小加1，并进入右子树。

六、代码示例

为了更好地理解顺序统计树中的OS-SELECT过程，我们将首先提供伪代码，然后给出C语言的实现。这将有助于读者理解如何在实际编程中应用这一过程。

6.1 OS-SELECT伪代码

Function OS-SELECT(Node x, Integer i)
    Rank = x.left.size + 1
    If i == Rank
        Return x
    ElseIf i < Rank
        // The i-th ranked element is in the left subtree
        Return OS-SELECT(x.left, i)
    Else
        // The i-th ranked element is in the right subtree
        Return OS-SELECT(x.right, i - Rank)

6.2 OS-SELECT的非递归版本伪代码

Function OS-SELECT-ITERATIVE(T, i)
    Current = T.root
    While Current ≠ NIL
        If i == 1
            Return Current
        EndIf
        Rank = Current.left.size + 1
        If i <= Rank
            // The i-th ranked element is in the left subtree
            Current = Current.left
        Else
            // The i-th ranked element is in the right subtree
            i = i - Rank
            Current = Current.right
        EndIf
    EndWhile
    Return NIL // If no element is found with the given rank

6.3 OS-SELECT的C语言实现

在C语言中，我们需要定义红黑树节点的结构体，并实现OS-SELECT过程。以下是一个简化的示例，它不包括完整的红黑树实现，但提供了OS-SELECT过程的核心逻辑。

#include <stdio.h>
#include <stdlib.h>

// 假设我们有一个红黑树节点的结构体定义如下：
typedef struct Node {
    int key; // 节点的关键字
    int size; // 以该节点为根的子树的大小
    int color; // 节点的颜色（红或黑）
    struct Node *left, *right, *parent;
} Node;

// 假设我们有一个红黑树的根节点指针
Node* T_root = NULL;

// OS-SELECT过程的C语言实现
Node* OS_SELECT(Node* x, int i) {
    int rank = x->left->size + 1;
    if (i == rank) {
        return x;
    } else if (i < rank) {
        // 在左子树中递归查找
        return OS_SELECT(x->left, i);
    } else {
        // 在右子树中查找
        return OS_SELECT(x->right, i - rank);
    }
}

// 非递归版本的OS-SELECT过程的C语言实现
Node* OS_SELECT_ITERATIVE(Node* T, int i) {
    Node* current = T;
    while (current != NULL) {
        int rank = current->left->size + 1;
        if (i == rank) {
            return current;
        } else if (i <= rank) {
            // 在左子树中查找
            current = current->left;
        } else {
            // 在右子树中查找
            i = i - rank;
            current = current->right;
        }
    }
    return NULL; // 如果没有找到元素，则返回NULL
}

// 主函数，用于测试OS-SELECT过程
int main() {
    // 这里应该包含红黑树的构建和初始化代码
    // ...

    // 假设我们要找到排名为10的元素
    Node* selected_node = OS_SELECT(T_root, 10);
    if (selected_node != NULL) {
        printf("The 10th ranked element is %d\n", selected_node->key);
    } else {
        printf("No element found with rank 10\n");
    }

    return 0;
}

请注意，上述C代码是一个简化的示例，它没有包括红黑树的完整实现，也没有处理红黑树插入和删除操作中的自平衡逻辑。在实际应用中，你需要一个完整的红黑树实现，包括节点的插入、删除、左旋、右旋以及颜色变更等操作，以确保树的平衡性。此外，上述代码也没有进行错误检查，例如检查输入的排名是否有效。在生产代码中，这些检查是必要的。

七、结论

顺序统计树通过在红黑树的每个节点上增加size属性，扩展了红黑树的功能，使其能够快速地处理顺序统计查询。OS-SELECT过程是一个高效的方法，用于在O(log n)的时间内找到排名为i的元素。非递归版本的OS-SELECT提供了一个递归方法的替代方案，可以在某些情况下避免栈溢出的问题。通过这些方法，我们可以有效地处理动态集合上的顺序统计操作，这在许多实际应用中是非常有用的。

顺序统计树在红黑树基础上的扩展与应用：OS-SELECT过程详解