一、几个概念
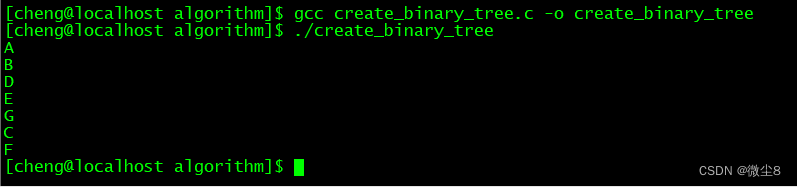
二叉树(binary tree):是 n(n >= 0)个结点(每个结点最多只有2棵子树)的有限集合,该集合可为空集(称为空二叉树),或由一个根节点和两颗互不相交的,称为根节点的左子树和右子树的二叉树组成。
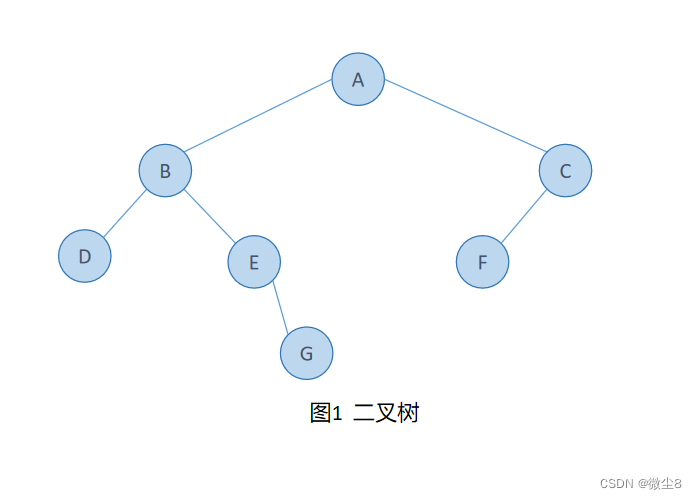
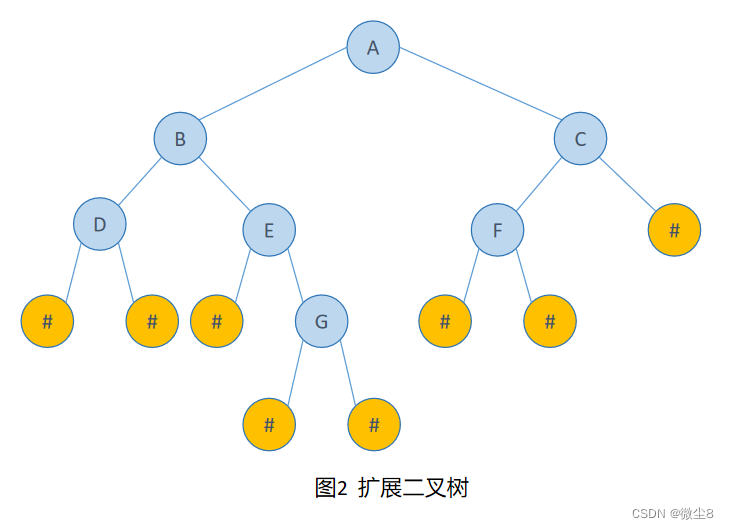
扩展二叉树:将二叉树中的每个结点的空子结点用一个虚拟结点表示,其值为一特定的值,比如"#",这样每个结点都有两个子结点,这种处理后的二叉树为原二叉树的扩展树。扩展二叉树就可以做到一个遍历序列确定一颗二叉树。
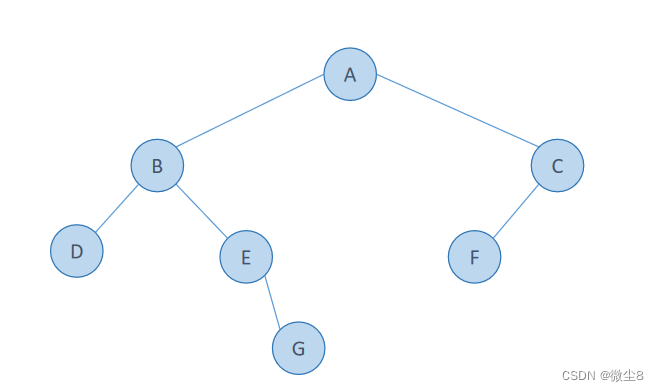
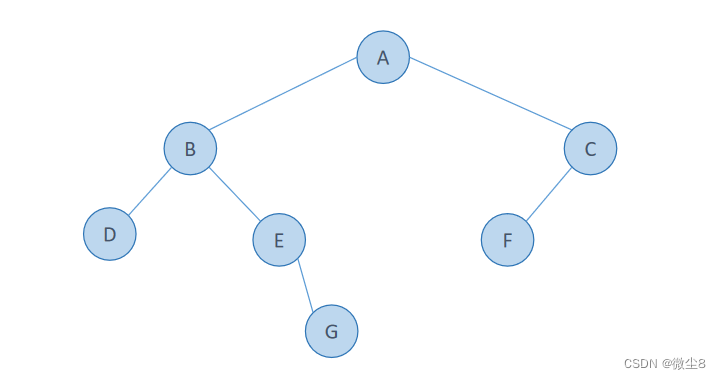
例如:图1为一颗二叉树,图2为这颗二叉树的扩展二叉树
前序遍历二叉树:先访问根结点,然后遍历左子树,最后遍历右子树
所以,图1这颗二叉树的前序遍历顺序为:ABDEGCF
这颗二叉树的扩展二叉树前序遍历序列为:ABD##E#G##CF###
二叉链表:是二叉树的一种链式存储结构,其中每个结点包含三个字段:一个数据字段(data)和两个指针字段(lchild、rchild),分别指向该结点的左孩子和右孩子。如果某个结点没有左孩子或右孩子,那么对应的指针字段为NULL。
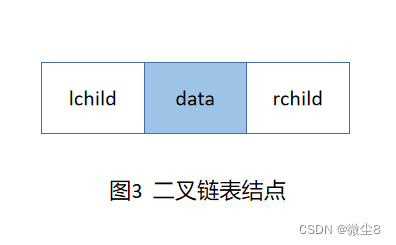
用 C 语言可以表述为:
typedef struct binary_node {
char data;
struct binary_node *lchild, *rchild;
}binary_tree;二、算法思路
扩展二叉树前序遍历序列创建二叉树过程:
(1)如果该结点为虚拟结点(即值 = '#'),则该结点为空
(2)如果该结点存在,则创建该结点,并把值赋给 data 字段,然后创建左子树,最后创建右子树
所以,这是一个递归的过程。
那么对于图2的扩展二叉树前序遍历序列:ABD##E#G##CF###
调用创建二叉树函数图解整个创建二叉树过程为:
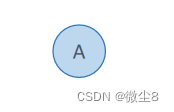
(1)调用创建二叉树函数,因为根结点的值为A,则创建该节点,并赋值该节点的 data = 'A'

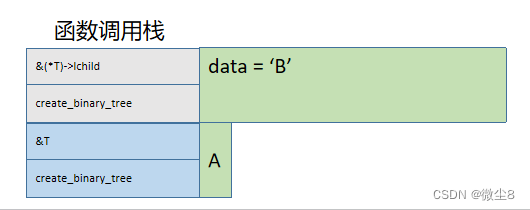
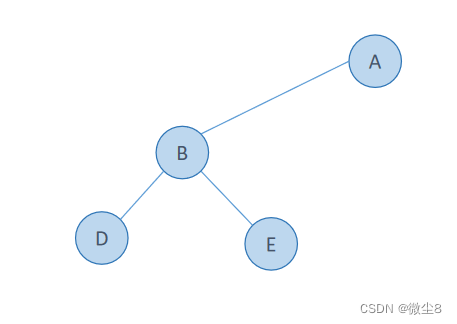
(2)调用创建二叉树函数创建A结点的左子树,因为该结点的值为B,则创建该结点,并赋值该结点的 data = 'B'

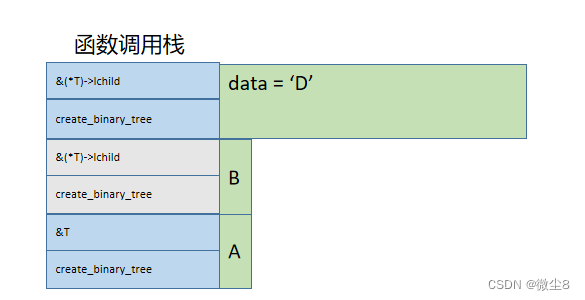
(3)调用创建二叉树函数创建B结点的左子树,因为该结点的值为D,则创建该结点,并赋值该结点的 data = 'D'

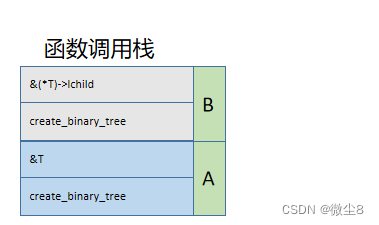
(4)调用创建二叉树函数创建D结点的左子树,因为该结点的值为#,则该结点为空,并赋值 lchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出


(5)调用创建二叉树函数创建D结点的右子树,因为该结点的值为#,则该结点为空,并赋值 rchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出


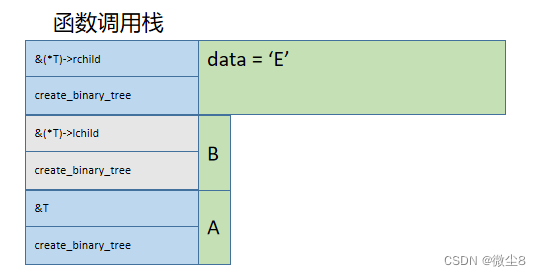
(6)此时创建结点D的 create_binary_tree 函数访问结点D和创建D结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出,然后,执行调用 create_binary_tree 函数创建结点B的右子树,因为该结点的值为E,则创建该结点,并赋值该结点的 data = 'E'
(7)调用创建二叉树函数创建E结点的左子树,因为该结点的值为#,则该结点为空,并赋值 lchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出

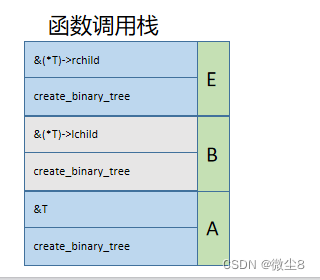
(8)调用创建二叉树函数创建E结点的右子树,因为该结点的值为G,则创建该结点,并赋值该结点的 data = 'G'
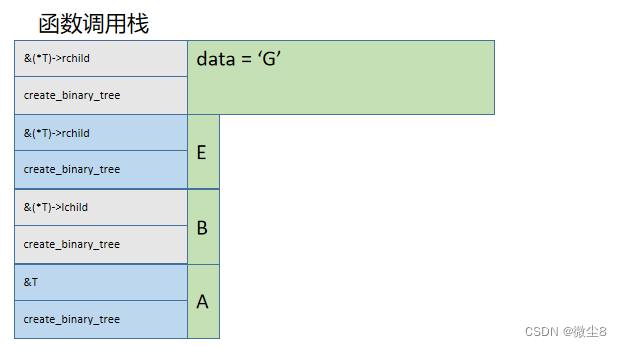
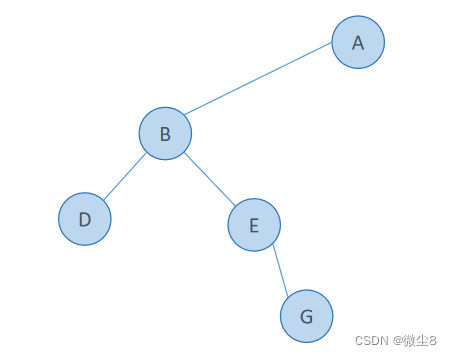
(9)调用创建二叉树函数创建G结点的左子树,因为该结点的值为#,则该结点为空,并赋值 lchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出

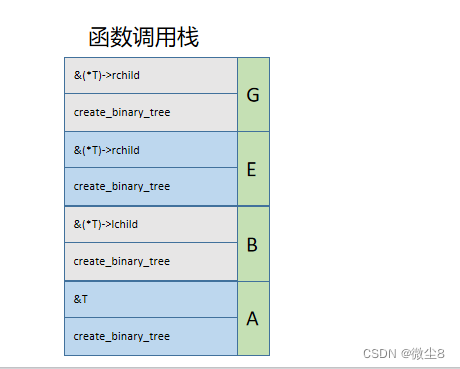
(10)调用创建二叉树函数创建G结点的右子树,因为该结点的值为#,则该结点为空,并赋值 rchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出
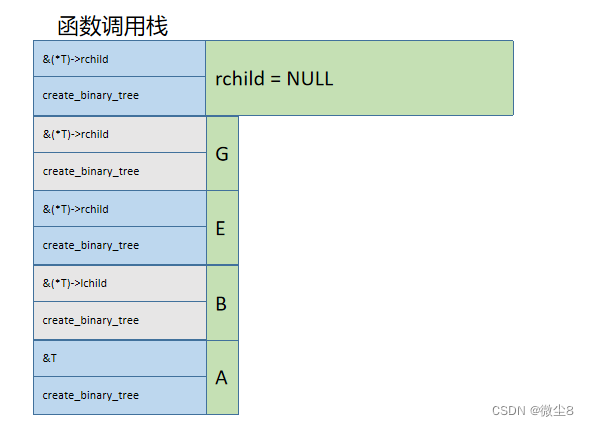

(11)此时创建结点G的 create_binary_tree 函数访问结点G和创建G结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。
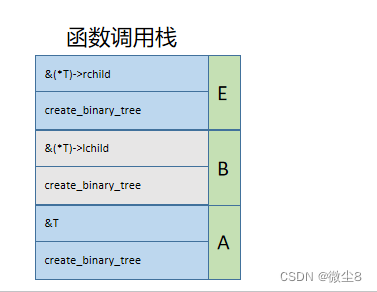
(12)此时创建结点E的 create_binary_tree 函数访问结点E和创建E结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。
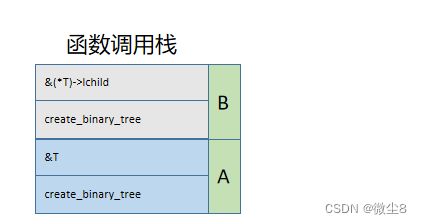
(13)此时创建结点B的 create_binary_tree 函数访问结点B和创建B结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。
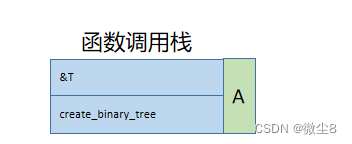
(14)调用创建二叉树函数创建A结点的右子树,因为该结点的值为C,则创建该结点,并赋值该结点的 data = 'C'
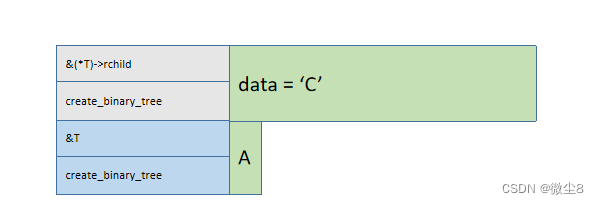

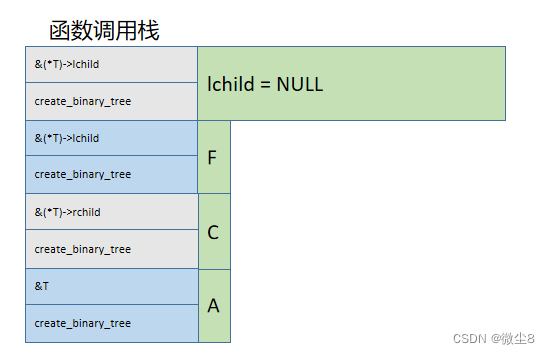
(15)调用创建二叉树函数创建C结点的左子树,因为该结点的值为F,则创建该结点,并赋值该结点的 data = 'F'
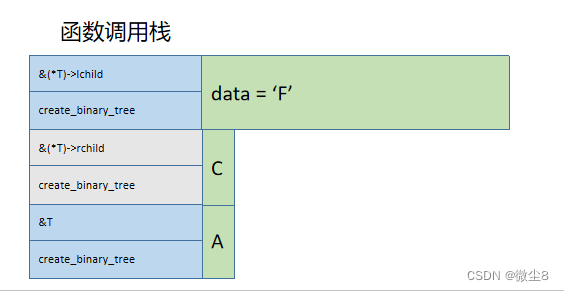
(16)调用创建二叉树函数创建F结点的左子树,因为该结点的值为#,则该结点为空,并赋值 lchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出
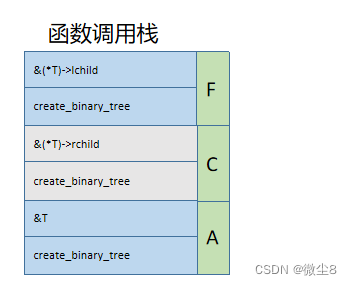
(16)调用创建二叉树函数创建F结点的右子树,因为该结点的值为#,则该结点为空,并赋值 rchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出


(17)此时创建结点F的 create_binary_tree 函数访问结点F和创建F结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。

(18)调用创建二叉树函数创建C结点的右子树,因为该结点的值为#,则该结点为空,并赋值 rchild = NULL,然后,栈顶的 create_binary_tree 函数执行完毕,从栈顶弹出
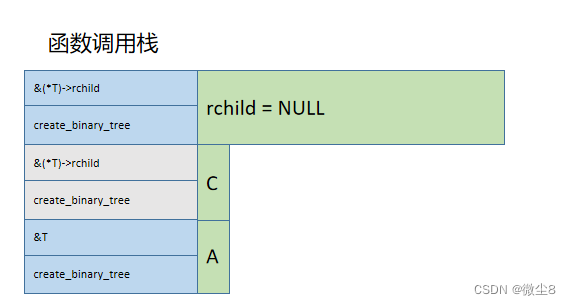

(19)此时创建结点C的 create_binary_tree 函数访问结点C和创建C结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。

(20)此时创建结点A的 create_binary_tree 函数访问结点A和创建A结点的左子树、右子树逻辑都已执行完毕,从栈顶弹出。至此,调用 create_binary_tree 函数创建二叉树函数逻辑都已执行完毕,整个函数返回,我们成功的用二叉树的扩展二叉树前序遍历序列构建二叉树如下所示
三、实现代码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct binary_node {
char data;
struct binary_node *lchild, *rchild;
}binary_tree;
//前序遍历扩展二叉树
char *g_str = "ABD##E#G##CF###";
int g_index = 0;
void create_binary_tree(binary_tree **T) {
if (strlen(g_str) == 0)
return;
if (g_str[g_index] == '#') {
T = NULL;
++g_index;
}
else {
*T = malloc(sizeof(**T));
(*T)->data = g_str[g_index];
(*T)->lchild = NULL;
(*T)->rchild = NULL;
++g_index;
create_binary_tree(&(*T)->lchild);
create_binary_tree(&(*T)->rchild);
}
}
void visit_node(binary_tree *T) {
printf("%c\n", T->data);
}
void pre_order_tree(binary_tree *T) {
if (!T)
return;
visit_node(T);
pre_order_tree(T->lchild);
pre_order_tree(T->rchild);
}
int main(int argc, char *argv[]) {
binary_tree *T = NULL;
create_binary_tree(&T);
pre_order_tree(T);
return 0;
}