大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述:
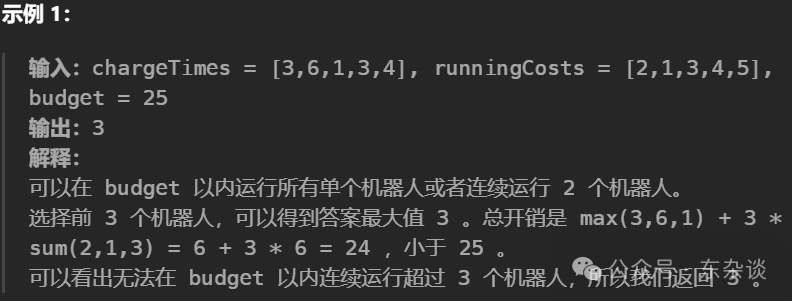
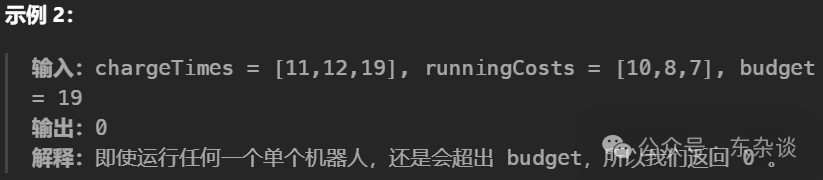
你有 n 个机器人,给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ,两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间,花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。
运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ,其中 max(chargeTimes) 是这 k 个机器人中最大充电时间,sum(runningCosts) 是这 k 个机器人的运行时间之和。
请你返回在 不超过 budget 的前提下,你 最多 可以 连续 运行的机器人数目为多少。
解题思路:
此问题的核心点在于求最多可以连续运行的机器人数目,也就是说要求最大连续子数组,明白这点之后我们就可以很快速的进行解题了
采用滑动窗口法(双指针)
滑动窗口:
-
使用双指针(滑动窗口)技巧来维护一个可以选择的机器人区间 [j, i]。j 是窗口的左边界,i 是窗口的右边界。
通过不断扩展右边界 i 来加入新的机器人,同时调整左边界 j 以确保在当前的区间内总成本不超过预算。
维护充电时间的最大值:
-
q:数组,用于存储当前窗口内的机器人的充电时间的索引,这些索引由 qb 和 qf 控制。
qb(Queue Back):队列的后指针,指向队列中下一个要插入新元素的位置(即下一个索引)。
qf(Queue Front):队列的前指针,指向队列中第一个元素的位置(即当前窗口的最大充电时间索引)。
使用一个双端队列(用数组模拟,q)来实时维护当前窗口内最大的充电时间。具体来说,在添加新的机器人时,队列中存储的是当前在窗口内机器人的索引,确保其对应的充电时间是单调递减的。
参考代码如下:
int maximumRobots(int* chargeTimes, int chargeTimesSize, int* runningCosts, int runningCostsSize, long long budget) {
int res = 0, n = chargeTimesSize;
long long runningCostSum = 0;
int* q = (int*)malloc(sizeof(int) * n), qf = 0, qb = 0;
for (int i = 0, j = 0; i < n; i++) {
runningCostSum += runningCosts[i];
while (qb > qf && chargeTimes[q[qb - 1]] <= chargeTimes[i]) {
qb--;
}
q[qb++] = i;
while (j <= i && (i - j + 1) * runningCostSum + chargeTimes[q[qf]] > budget) {
if (qb > qf && q[qf] == j) {
qf++;
}
runningCostSum -= runningCosts[j];
j++;
}
res = fmax(res, i - j + 1);
}
free(q);
return res;
}时间复杂度:
代码总体时间复杂度主要受到两个循环的影响:
1. 外层循环 (`for (int i = 0, j = 0; i < n; i++)`):
- 该循环遍历所有机器人,因此它的时间复杂度为 O(n),其中 n 是 `chargeTimes` 的大小。
2. 内层循环:
- 第一个内层循环 `while (qb > qf && chargeTimes[q[qb - 1]] <= chargeTimes[i])`:
- 此循环用于维护存储充电时间索引的队列 `q`,确保队列中的元素是单调递减的。在最坏情况下,每个元素在这个队列中可能会被添加和移除一次,因此这个循环的时间复杂度是 O(1),因为对于每个 `i`,这段代码最多只会遍历它当时有效的 `qb`。
- 第二个内层循环 `while (j <= i && (i - j + 1) * runningCostSum + chargeTimes[q[qf]] > budget)`:
- 该循环用于调整窗口的左边界 `j`,以确保当前窗口内的开销不超过预算。
- 在这个过程中,随着 `j` 的每次增加,`runningCostSum` 会减少。因此,对于每个外层的 `i`,`j` 也最多只遍历一次整个数组,总体来说这个循环的时间复杂度也是 O(n)。
综上所述,两个循环的合并可以在最坏情况下产生 O(n) 的复杂度。因此,代码的总的时间复杂度为 O(n)。
空间复杂度:
代码中的空间复杂度主要由以下几个因素组成:
1. 空间用于存储队列 `q`:
- `q` 是一个整数数组,包含最多 `n` 个索引,因此使用 O(n) 的空间。
2. 其他变量:
- 变量 `res`、`n`、`runningCostSum`、`qf` 和 `qb` 均为常量大小,使用 O(1) 的空间。
综上所述,空间复杂度主要是由于 `q` 的存在,整体空间复杂度为 O(n)。
结论
- 时间复杂度:O(n)
- 空间复杂度:O(n)