前缀和与差分

发布于：2025-02-10 ⋅ 阅读:(99) ⋅ 点赞:(0)

一.前缀和

为什么需要前缀和，假设你现在让你计算在任意区间【l，r】m次

暴力做法：

时间复杂度o(m*n)

那现在我们就来介绍前缀和

1.原理和特点

presum表示前缀和，前缀和由一个用户输入的数组生成。

用一个presum数组预处理记录每一段a数组的值

对于一个数组a[](下标从1开始)，定义一个前缀和数组presum[],满足： $presum[i]=\sum_{j=1}^{i}a[j]$

presum有一个重要特征，可用于快速生成presum：

$presum[i]=\sum_{j=1}^{i-1}a[j]+a[i]=presum[i-1]+a[i]$

2.求区间和

presum可以o（1）的求某一段区间和：

sum[l,r]=presum[r]-presum[l-1]

3.适用范围

presum只适合a为静态数组的情况下，即a数组元素在查询过程中不会进行修改

4.实现

4.1前缀和数组实现

for (int i = 1; i <= n; i++)
{
	presum[i] = presum[i - 1] + a[i];//尽量把a[]和presum[]写为全局变量 因为前缀和默认a[0]和presum[0]为0
}

4.2区间和实现

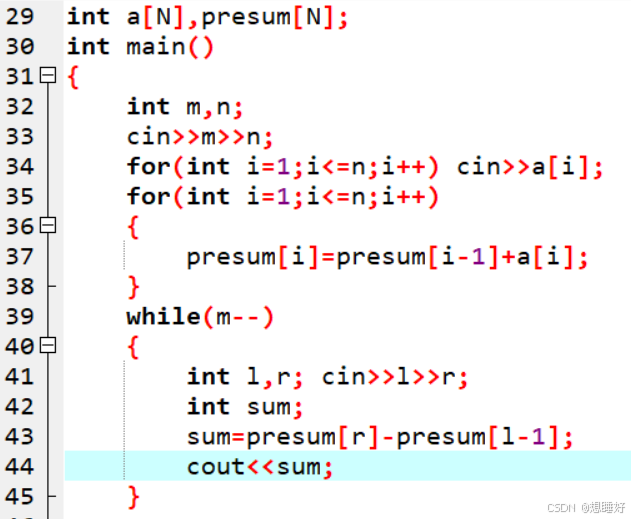
可以明显看到时间复杂度变为O（m+n）

二.例题

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
char s[N];
int presum[N];
int main()
{
  cin>>s+1;//前缀和从s[1]开始
  int n=strlen(s+1);//长度从1开始计算
  for(int i=1;i<=n;i++)
  presum[i]=presum[i-1]+(s[i]=='L'?1:-1);//笔记第一步
  int maxcount=0;
  for(int i=1;i<=n;i++)
  for(int j=i;j<=n;j++)
  if(presum[j]-presum[i-1]==0) maxcount=max(maxcount,j-i+1);//笔记第二步
  cout<<maxcount;
}