目录
七、累积分布函数图(Cumulative Distribution Function,CDF图)
一、直方图(Histogram)
1.定义
直方图是一种用于展示数据分布的柱状图。它将数据划分为若干个连续、不重叠的区间(称为“桶”或“bin”),并统计每个区间内的数据点数量。直方图通过柱状的高度来表示每个区间内的数据频数,从而直观地展示数据的分布情况。
2.特点
直观性:通过柱状图的形式,可以直观地展示数据的集中趋势、分散程度和偏态情况。
灵活性:可以通过调整bin的宽度和数量,更细致或更宏观地观察数据分布。
多用途:适用于单变量数据的分布分析,能够帮助识别数据中的异常值或分布的异常情况。
3.局限性
依赖bin的划分:bin的宽度和数量的选择会影响直方图的形状,可能导致对数据分布的误解。如果bin太宽,可能会掩盖数据的细节;如果bin太窄,可能会引入噪声。
不适用于小数据集:数据量较小时,直方图可能无法准确反映数据的真实分布。
无法展示连续分布:直方图只能展示数据在各个区间的频数,无法展示数据的连续分布情况。
4.类型
简单直方图:最基本的直方图,展示数据在各个区间的频数。
堆叠直方图:用于展示多个数据集的分布情况,通过堆叠的方式将不同数据集的柱状图叠加在一起。
并排直方图:用于展示多个数据集的分布情况,通过并排的方式将不同数据集的柱状图并排放置。
频率直方图:展示每个区间的频率(相对频数),而不是频数。
累积直方图:展示每个区间的累积频数或累积频率。
5.应用场景
数据分析:用于分析单变量数据的分布情况,例如考试成绩分布、商品价格分布、用户年龄分布等。
数据预处理:帮助识别数据中的异常值或数据分布的异常情况,为后续的数据处理提供依据。
质量控制:在生产过程中,用于分析产品质量指标的分布情况,判断生产过程是否稳定。
市场研究:分析消费者行为数据的分布情况,例如购买金额、购买频率等。
6.使用Python实现
使用Matplotlib绘制直方图。
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data = np.random.randn(1000) # 生成1000个正态分布的随机数
# 绘制简单直方图
plt.hist(data, bins=30, edgecolor='black', alpha=0.7, color='blue')
plt.title('Simple Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
结果:生成一个简单直方图,展示数据的分布情况,柱状图的高度表示每个bin内的数据点数量。
绘制堆叠直方图。堆叠直方图用于展示多个数据集的分布情况,通过堆叠的方式将不同数据集的柱状图叠加在一起。
#堆叠直方图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2 # 偏移2个单位
# 绘制堆叠直方图
plt.hist([data1, data2], bins=30, stacked=True, edgecolor='black', label=['Data 1', 'Data 2'])
plt.title('Stacked Histogram')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.legend()
plt.show()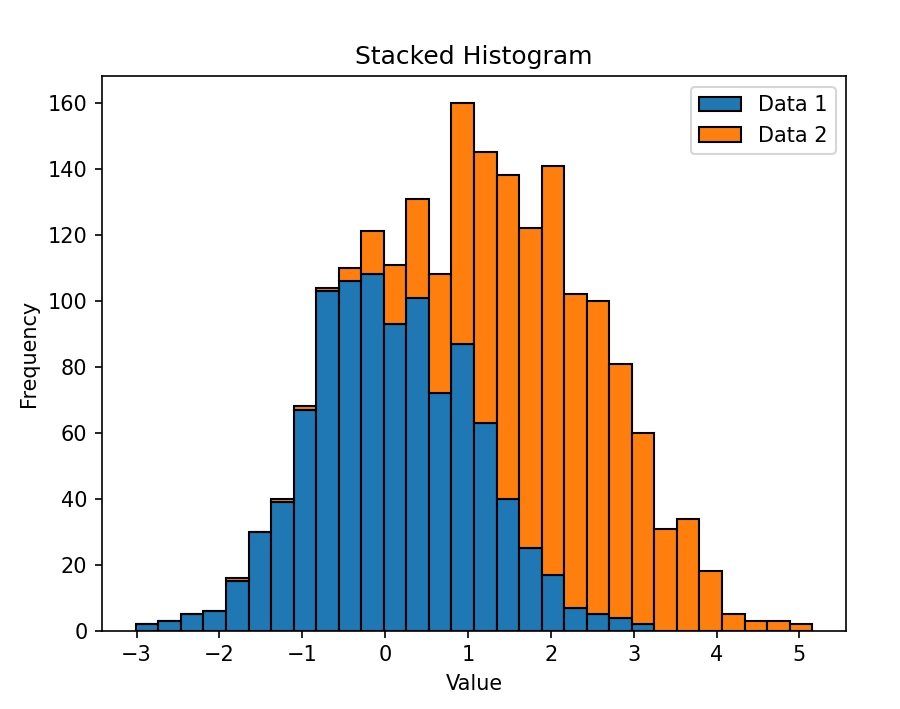
结果:生成一个堆叠直方图,展示两个数据集的分布情况,不同数据集的柱状图通过堆叠的方式叠加在一起。
二、密度图(Density Plot)
1.定义
密度图是一种基于核密度估计(Kernel Density Estimation, KDE)的可视化方法,用于展示数据的概率密度分布。它通过平滑处理数据点,生成一条连续的曲线,从而更直观地展示数据的分布特征。密度图的核心思想是将每个数据点视为一个“核”,并通过核函数对数据点进行平滑处理,最终得到一个连续的概率密度函数。
2.特点
平滑性:相比直方图,密度图更加平滑,能够更直观地展示数据的连续分布情况。
灵活性:可以通过调整核函数和带宽参数来优化密度曲线的形状,以更好地适应数据的分布特征。
直观性:能够清晰地展示数据的集中趋势、分散程度和偏态情况。
多用途:适用于展示连续数据的概率分布,尤其适用于数据点较多且分布较为复杂的情况。
3.局限性
依赖参数选择:核函数和带宽参数的选择会影响密度曲线的形状,可能导致对数据分布的误解。如果带宽过大,可能会掩盖数据的真实分布;如果带宽过小,可能会引入噪声。
计算复杂度:对于大数据集,核密度估计的计算复杂度较高,可能会影响性能。
不适用于离散数据:密度图主要用于展示连续数据的分布,对于离散数据可能不太适用。
4.类型
单变量密度图:用于展示单个变量的概率密度分布。
多变量密度图:用于展示多个变量的概率密度分布,可以通过堆叠或并排的方式展示不同变量的密度曲线。
二维密度图:用于展示两个变量的联合概率密度分布,通常通过等高线图或热力图来表示。
5.应用场景
数据分析:用于展示连续数据的概率分布,帮助识别数据的集中趋势、分散程度和偏态情况。
数据比较:可以用于比较不同组数据的分布差异,例如不同性别或不同年龄段的收入分布。
机器学习:在数据预处理阶段,帮助理解数据的分布特征,为后续的建模提供依据。
统计分析:用于展示数据的分布情况,辅助进行假设检验和模型拟合。
6.使用Python实现
使用Matplotlib绘制单变量密度图
#密度图
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
# 示例数据
data = np.random.randn(1000) # 生成1000个正态分布的随机数
# 计算核密度估计
kde = gaussian_kde(data)
x = np.linspace(min(data), max(data), 1000)
density = kde(x)
# 绘制密度图
plt.plot(x, density, color='blue', label='Density')
plt.title('Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show() 结果:生成一条平滑的密度曲线,展示数据的概率密度分布。
结果:生成一条平滑的密度曲线,展示数据的概率密度分布。
使用Seaborn绘制多变量密度图。Seaborn的kdeplot函数支持多变量数据,可以通过堆叠或并排的方式展示不同变量的密度曲线。
#多变量密度图
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt # 添加这行导入
# 示例数据
data1 = np.random.randn(1000) # 生成1000个正态分布的随机数
data2 = np.random.randn(1000) + 2 # 偏移2个单位
# 绘制多变量密度图
sns.kdeplot(data1, fill=True, color='blue', label='Data 1')
sns.kdeplot(data2, fill=True, color='orange', label='Data 2')
plt.title('Multi - variable Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()
结果:生成两条平滑的密度曲线,分别展示两个数据集的概率密度分布,并填充曲线下的区域。
三、箱线图(Box Plot)
1.定义
箱线图(Box Plot),也称为箱须图(Box-and-Whisker Plot),是一种用于展示一组数据的五数概括(最小值、第一四分位数、中位数、第三四分位数和最大值)的可视化方法。它通过一个矩形框(箱体)和若干条线(须线)来表示数据的分布范围和集中趋势。箱线图能够直观地展示数据的中位数、四分位数范围(IQR)、异常值以及数据的偏态情况。
2.特点
五数概括:清晰地展示数据的最小值、第一四分位数(Q1)、中位数(Q2)、第三四分位数(Q3)和最大值。
直观性:通过箱体的大小和位置,可以直观地比较不同组数据的分布差异。
异常值检测:能够识别数据中的异常值(通常定义为超出1.5倍四分位距范围的点)。
偏态展示:通过箱体和须线的不对称性,可以直观地判断数据的偏态情况。
3.局限性
信息有限:仅展示五数概括,无法反映数据的详细分布情况,例如双峰分布等。
依赖数据量:对于小数据集,箱线图可能无法准确反映数据的真实分布。
异常值定义主观性:异常值的定义(通常是1.5倍IQR)是主观的,可能不适用于所有数据集。
4.类型
简单箱线图:展示单组数据的五数概括。
分组箱线图:用于展示多组数据的分布情况,通过并排的方式展示不同组的箱线图。
带点箱线图:在箱线图的基础上,展示原始数据点,便于更直观地观察数据分布。
5.应用场景
数据分析:用于分析数据的分布特征,尤其是数据的集中趋势和离散程度。
数据比较:在多组数据的比较中,能够快速识别出异常值和数据分布的偏态情况。
质量控制:在生产过程中,用于分析产品质量指标的分布情况,判断生产过程是否稳定。
统计分析:用于展示数据的分布情况,辅助进行假设检验和模型拟合。
6.使用Python实现
使用Matplotlib绘制简单箱线图
 结果:生成一个简单箱线图,展示数据的五数概括,箱体表示四分位数范围,须线表示数据的分布范围,点表示异常值。
结果:生成一个简单箱线图,展示数据的五数概括,箱体表示四分位数范围,须线表示数据的分布范围,点表示异常值。
使用Seaborn绘制分组箱线图
import seaborn as sns
import numpy as np
import pandas as pd
# 示例数据
data1 = np.random.randn(100)
data2 = np.random.randn(100) + 2 # 偏移2个单位
df = pd.DataFrame({'Value': np.concatenate([data1, data2]),
'Group': ['Group 1'] * 100 + ['Group 2'] * 100})
# 绘制分组箱线图
sns.boxplot(x='Group', y='Value', data=df, palette='Set2')
plt.title('Grouped Box Plot')
plt.ylabel('Value')
plt.show()
结果:生成一个分组箱线图,展示两组数据的分布情况,通过并排的方式展示不同组的箱线图。
四、小提琴图(Violin Plot)
1.定义
小提琴图是一种结合了箱线图(Box Plot)和密度图(Density Plot)的可视化工具。它在箱线图的基础上,增加了两侧的密度曲线,用于展示数据的概率密度分布。小提琴图通过箱线图展示数据的五数概括(最小值、第一四分位数、中位数、第三四分位数和最大值),并通过密度曲线展示数据的连续分布情况。
2.特点
综合展示:结合了箱线图和密度图的优点,既能展示数据的五数概括,又能展示数据的连续分布情况。
直观性:通过小提琴的宽度,可以直观地看出数据在不同值范围内的密度大小,帮助识别数据的集中趋势和离散程度。
异常值检测:与箱线图类似,小提琴图也可以展示异常值。
多组数据比较:可以并排展示多组数据的小提琴图,便于比较不同组数据的分布差异。
3.局限性
依赖参数选择:密度曲线的形状依赖于核函数和带宽参数的选择,可能导致对数据分布的误解。
信息过载:在展示多组数据时,小提琴图可能会显得过于拥挤,尤其是当数据组数较多时。
4.类型
简单小提琴图:展示单组数据的分布情况。
分组小提琴图:并排展示多组数据的分布情况,便于比较不同组之间的差异。
堆叠小提琴图:将多组数据的小提琴图堆叠在一起,展示数据的层次结构。
5.应用场景
数据分析:用于展示复杂数据的分布情况,尤其适用于数据分布不均匀或存在多个峰值的情况。
数据比较:在多组数据的比较中,能够更全面地展示数据的分布特征和差异。
统计分析:用于展示数据的分布情况,辅助进行假设检验和模型拟合。
机器学习:在数据预处理阶段,帮助理解数据的分布特征,为后续的建模提供依据。
6.使用Python实现
使用Matplotlib绘制简单小提琴图
#小提琴图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data = np.random.randn(100) # 生成100个正态分布的随机数
# 绘制简单小提琴图
plt.violinplot(data, showmeans=True, showmedians=True)
plt.title('Simple Violin Plot')
plt.ylabel('Value')
plt.show()
结果:生成一个简单小提琴图,展示数据的五数概括和密度分布情况。
使用Matplotlib绘制分组小提琴图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data1 = np.random.randn(100)
data2 = np.random.randn(100) + 2 # 偏移2个单位
data = [data1, data2]
# 绘制分组小提琴图
plt.violinplot(data, showmeans=True, showmedians=True)
plt.title('Grouped Violin Plot')
plt.ylabel('Value')
plt.xticks([1, 2], ['Group 1', 'Group 2'])
plt.show()
结果:生成一个分组小提琴图,展示两组数据的分布情况,通过并排的方式展示不同组的小提琴图。
五、热力图(Heatmap)
1.定义
热力图是一种用于展示二维数据分布的可视化方法,通过颜色的变化来表示数据的大小或密度。它通常用于展示矩阵数据或二维表格数据,例如相关性矩阵、地理数据分布、时间序列数据等。热力图的核心思想是将数据映射到颜色的渐变上,从而直观地展示数据的分布模式和相关性。
2.特点
直观性:通过颜色的渐变,可以快速识别数据的高低和聚集区域。
多用途:适用于展示相关性矩阵、地理数据分布、时间序列数据等多种二维数据。
灵活性:可以通过调整颜色映射、添加注释等方式增强可视化效果。
数据比较:可以同时展示多个变量之间的关系,便于比较和分析。
3.局限性
信息过载:当数据量较大或变量较多时,热力图可能会显得过于拥挤,难以清晰地展示细节。
依赖颜色选择:颜色映射的选择会影响热力图的可读性,不恰当的颜色选择可能导致误解。
不适合展示非矩阵数据:热力图主要用于展示矩阵数据,对于非矩阵数据可能不太适用。
4.类型
相关性热力图:用于展示变量之间的相关性,通常用于统计分析。
地理热力图:用于展示地理数据的分布情况,例如人口密度、温度分布等。
时间序列热力图:用于展示时间序列数据的变化趋势,例如每日温度、股票价格等。
矩阵热力图:用于展示任意二维矩阵数据,例如用户行为数据、基因表达数据等。
5.应用场景
地理分析:用于展示地理数据的分布情况,例如人口密度、温度分布等。
时间序列分析:用于展示时间序列数据的变化趋势,帮助识别周期性和异常点。
用户行为分析:用于展示用户行为数据的分布情况,例如网站访问量、用户点击率等。
6.使用Python实现
使用Matplotlib绘制相关性热力图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据:生成一个相关性矩阵
data = np.random.randn(10, 10)
corr_matrix = np.corrcoef(data)
# 绘制热力图
plt.imshow(corr_matrix, cmap='coolwarm', interpolation='nearest')
plt.colorbar(label='Correlation')
plt.title('Correlation Heatmap')
plt.xlabel('Variable Index')
plt.ylabel('Variable Index')
plt.show()结果:生成一个相关性热力图,展示变量之间的相关性。颜色的深浅表示相关性的强弱。
使用Seaborn绘制地理热力图
import seaborn as sns
import numpy as np
import pandas as pd
# 示例数据:生成一个地理数据矩阵
data = np.random.rand(10, 10) * 100 # 假设数据范围为0到100
df = pd.DataFrame(data, columns=[f"Long {i}" for i in range(10)],
index=[f"Lat {i}" for i in range(10)])
# 绘制地理热力图
sns.heatmap(df, annot=True, fmt=".1f", cmap='viridis', linewidths=0.5)
plt.title('Geographical Heatmap')
plt.show()
结果:生成一个地理热力图,展示地理数据的分布情况。颜色的深浅表示数据的大小。
六、蜂群图
1.定义
蜂群图是一种点图的变体,它通过将数据点沿着一个轴排列,并在另一个轴上进行微小的偏移,以避免重叠。这种排列方式使得每个数据点都能清晰地展示出来,同时保留了数据的分布信息。蜂群图特别适合展示具有多个类别的数据分布情况。
2.特点
清晰展示数据点:通过微小的偏移,避免了数据点的重叠,使得每个数据点都能清晰地展示出来。
保留分布信息:与箱线图或小提琴图相比,蜂群图保留了每个数据点的具体信息,而不是仅仅展示统计量。
适用于小数据集:对于数据量较小的数据集,蜂群图能够有效地展示数据的分布情况。
灵活性:可以通过调整点的大小、颜色和形状,增强可视化效果。
3.局限性
不适用于大数据集:当数据量较大时,蜂群图可能会显得过于拥挤,难以清晰地展示每个数据点。
依赖数据分布:如果数据分布过于密集,蜂群图可能会失去其优势,甚至导致视觉上的混乱。
信息有限:虽然蜂群图能够展示每个数据点,但它无法像箱线图或小提琴图那样直接展示数据的统计量(如中位数、四分位数等)。
4.类型
简单蜂群图:展示单组数据的分布情况。
分组蜂群图:并排展示多组数据的分布情况,便于比较不同组之间的差异。
堆叠蜂群图:将多组数据的蜂群图堆叠在一起,展示数据的层次结构。
5.应用场景
数据分析:用于展示数据的分布情况,特别适合小数据集。
数据比较:在多组数据的比较中,能够清晰地展示每个数据点的位置,便于识别差异。
统计分析:用于展示数据的分布情况,辅助进行假设检验和模型拟合。
机器学习:在数据预处理阶段,帮助理解数据的分布特征,为后续的建模提供依据。
6.使用Python实现
使用Matplotlib绘制简单蜂群图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data = np.random.randn(500) # 生成500个正态分布的随机数
# 计算偏移量
jitter = np.random.uniform(-0.1, 0.1, size=len(data))
# 绘制蜂群图
plt.scatter(jitter, data, alpha=0.7, color='blue')
plt.title('Simple Beeswarm Plot')
plt.xlabel('Category')
plt.ylabel('Value')
plt.show()
结果:生成一个简单蜂群图,展示数据的分布情况,每个数据点通过微小的偏移避免重叠。
使用Seaborn绘制分组蜂群图
import seaborn as sns
import matplotlib.pyplot as plt
# 加载Seaborn自带的tips数据集
tips = sns.load_dataset('tips')
# 绘制蜂群图,按' day'(星期几)分组,展示'tip'(小费金额),并根据'smoker'(是否吸烟)进行颜色区分
sns.swarmplot(x='day', y='tip', hue='smoker', data=tips)
plt.title('Grouped Beeswarm Plot of Tips')
plt.xlabel('Day of the Week')
plt.ylabel('Tip Amount')
plt.legend(title='Smoker')
plt.show()
结果:生成一个分组蜂群图,展示四组数据的分布情况,通过并排的方式展示不同组的蜂群图。
七、累积分布函数图(Cumulative Distribution Function,CDF图)
1.定义
累计分布图(CDF)是一种用于展示数据分布的函数图,它表示数据值小于或等于某个特定值的概率。CDF是一个单调递增的函数,其值域在0,1之间。对于一个随机变量X,其累计分布函数F(x)定义为: F(x)=P(X≤x) CDF图通过绘制x值与对应的F(x)值,直观地展示了数据的分布情况。
2.特点
直观性:CDF图能够直观地展示数据值的累积概率,帮助理解数据的分布范围和集中程度。
单调性:CDF图是一个单调递增的函数,其值域在0,1之间,便于比较不同数据集的分布。
灵活性:可以通过调整数据的分组或分段,展示不同粒度的累积分布情况。
3.局限性
信息有限:CDF图主要展示累积概率,无法像直方图或密度图那样直观地展示数据的具体分布形状。
依赖数据量:对于小数据集,CDF图可能不够平滑,难以准确反映数据的真实分布。
不适用于多变量比较:CDF图主要用于单变量数据的分析,对于多变量数据的比较,可能需要绘制多个CDF图,导致信息过载。
4.类型
简单CDF图:展示单个数据集的累积分布情况。
分组CDF图:并排或堆叠展示多个数据集的累积分布情况,便于比较不同组之间的差异。
经验CDF图:基于实际数据计算的CDF图,通常用于展示样本数据的分布情况。
5.应用场景
数据分析:用于展示数据的分布范围和累积概率,帮助识别数据的集中趋势和离散程度。
统计分析:用于计算分位数(如中位数、四分位数等),评估数据的偏态和离散程度。
质量控制:在生产过程中,用于分析产品质量指标的分布情况,判断生产过程是否稳定。
6.使用Python实现
使用Matplotlib绘制简单CDF图
import matplotlib.pyplot as plt
import numpy as np
# 示例数据
data = np.random.randn(1000) # 生成1000个正态分布的随机数
# 计算累积分布函数
counts, bin_edges = np.histogram(data, bins=30)
cdf = np.cumsum(counts) / np.sum(counts)
# 绘制CDF图
plt.plot(bin_edges[1:], cdf, marker='.', linestyle='-', color='b')
plt.title('Cumulative Distribution Function (CDF)')
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.grid(True)
plt.show() 结果:生成一个简单的CDF图,展示数据的累积分布情况
结果:生成一个简单的CDF图,展示数据的累积分布情况
使用Seaborn绘制分组经验CDF图
import seaborn as sns
import numpy as np
import pandas as pd
# 示例数据
data1 = np.random.randn(1000)
data2 = np.random.randn(1000) + 2 # 偏移2个单位
df = pd.DataFrame({'Value': np.concatenate([data1, data2]),
'Group': ['Group 1'] * 1000 + ['Group 2'] * 1000})
# 绘制分组经验CDF图
sns.ecdfplot(data=df, x='Value', hue='Group', palette='Set2')
plt.title('Grouped Empirical Cumulative Distribution Function (ECDF)')
plt.xlabel('Value')
plt.ylabel('Cumulative Probability')
plt.grid(True)
plt.show()
结果:生成一个分组经验CDF图,展示两组数据的累积分布情况。Seaborn会自动处理数据的分组和累积概率的计算。
八、总结
图表 类型 |
特点 | 适用场景 | 局限性 |
|---|---|---|---|
| 直方图 | 直观呈现数据频数分布,可看出数据集中和分散情况 | 展示单变量数据分布,如学生成绩区间分布、产品尺寸分布 | 分组方式影响展示效果,对数据变化趋势展示不足 |
| 密度图 | 平滑展示数据分布,可对比多组数据分布形状,不受分组影响 | 分析连续型数据分布,如不同地区气温分布对比 | 难以精确读取具体数值,对数据量小的情况可能不准确 |
| 箱线图 | 可直观展示数据分布范围、偏态、离散程度及异常值,便于多组数据比较 | 比较多组数据分布,如不同班级成绩分布对比 | 不能详细展示数据分布形状,对分布细节展示有限 |
| 小提琴图 | 兼具箱线图和密度图优势,全面展示数据分布特征,如中心位置、离散程度、分布形状 | 展示多组数据分布特征,对比不同类别数据分布 | 绘制相对复杂,数据量过大时可能视觉上较杂乱 |
| 热力图 | 能快速展示数据间差异和相似性,直观呈现数据分布模式 | 展示矩阵数据(如相关性矩阵、时间序列数据矩阵)、地理空间数据分布,如店铺在不同区域的热度分布 | 颜色映射可能造成视觉误差,难以展示数据具体数值 |
| 蜂群图 | 可展示大量数据点分布,能清晰看到每个数据点位置,体现数据实际取值 | 展示分组数据分布,查看组内数据离散情况,如不同部门员工绩效得分分布 | 数据点过多时可能重叠,影响观察,不适合展示数据整体分布趋势 |
| 累积分布图 | 可直观了解数据在某个值以下的累积概率,判断数据分布特征,如是否符合某种理论分布 | 检验数据分布类型,分析数据累积概率,如判断产品寿命是否符合指数分布 | 不能展示数据分布细节,如峰值位置等 |
