目录
1.算法运行效果图预览
(完整程序运行后无水印)
2.算法运行软件版本
matlab2024b
3.部分核心程序
(完整版代码包含详细中文注释和操作步骤视频)
.......................................................................
for loop = 1:length(YTest(1, :))
disp(loop); % 显示当前循环次数
temp = classify(net, XTest(:,:,:,:,loop)); % 对测试数据进行分类
for n = 1:length(temp)
if YTest(n, loop) == 'ON'
if temp(n) ~= YTest(n, loop)
FDR(loop) = FDR(loop) + 1; % 误检次数加 1
end
cnt1 = cnt1 + 1; % ON 状态计数器加 1
else
if temp(n) ~= YTest(n, loop)
MDR(loop) = MDR(loop) + 1; % 漏检次数加 1
end
cnt2 = cnt2 + 1; % OFF 状态计数器加 1
end
end
FDR(loop) = FDR(loop) / cnt1; % 计算误检率
MDR(loop) = MDR(loop) / cnt2; % 计算漏检率
ACC(loop) = 1 - sum(temp ~= YTest(:, loop)) / length(temp); % 计算准确率
end
SNR = -20:2:6; % 信噪比范围
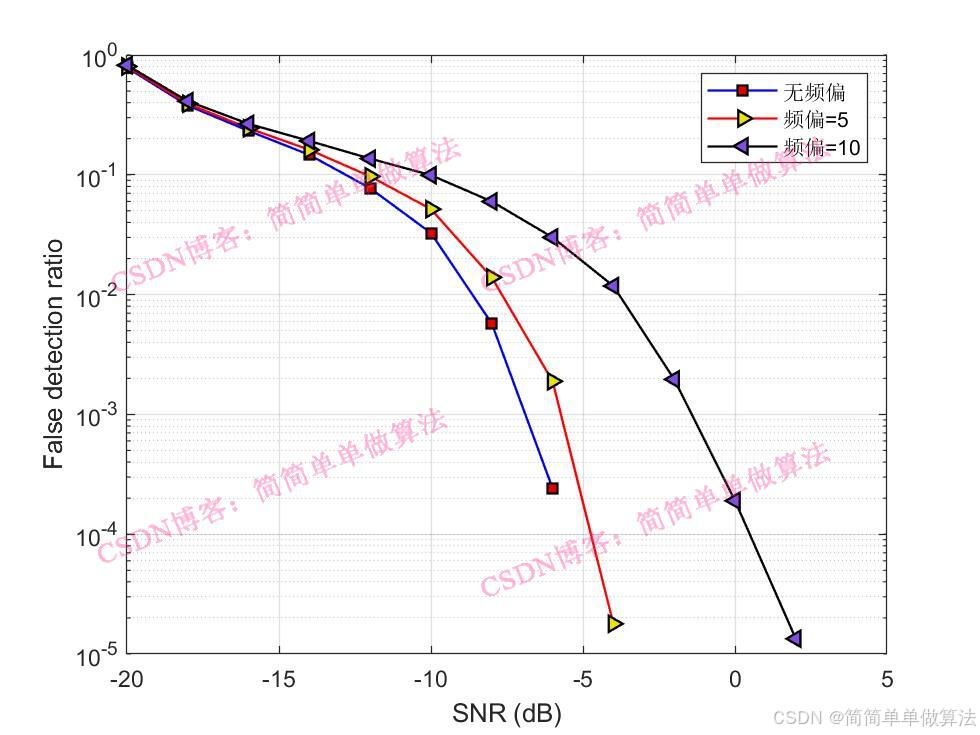
% 绘制误检率和漏检率图
figure;
semilogy(SNR, FDR, 'bo-', 'LineWidth', 2); % 绘制误检率曲线
hold on;
grid on;
title('Miss & False'); % 图标题
xlabel('SNR (dB)'); % x 轴标签
ylabel('Probability'); % y 轴标签
legend('False detection ratio'); % 图例
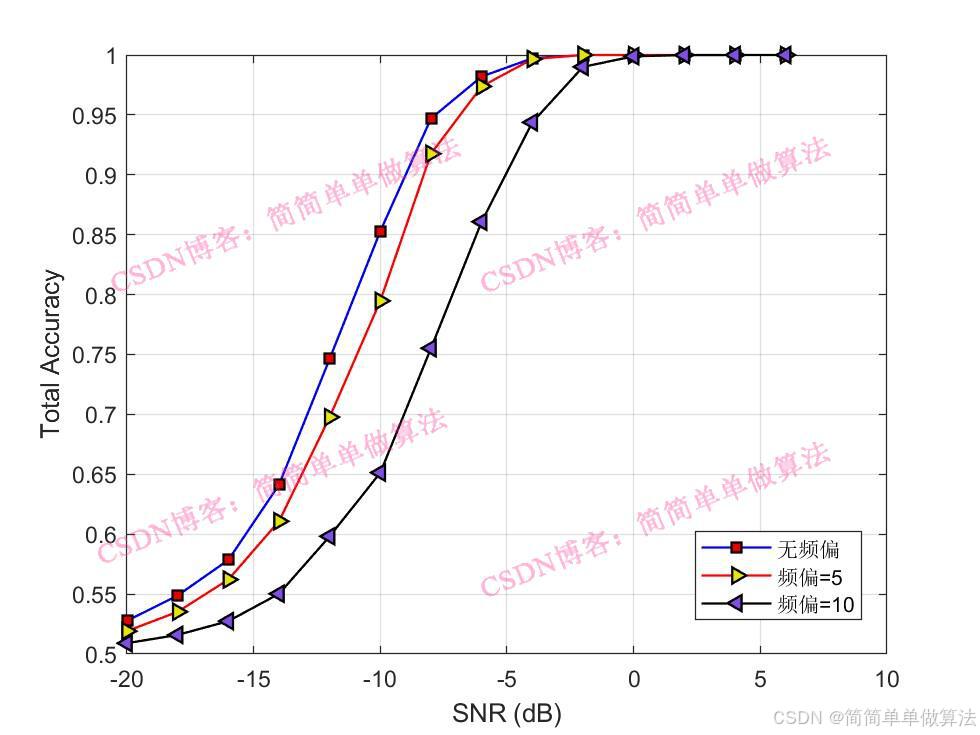
% 绘制准确率图
figure;
plot(SNR, ACC, 'bo-', 'LineWidth', 2); % 绘制准确率曲线
grid on;
xlabel('SNR (dB)'); % x 轴标签
ylabel('Total Accuracy'); % y 轴标签
% 保存结果
if sel==1
save R1.mat FDR ACC SNR; % 保存 QPSK 的结果
end
if sel==2
save R2.mat FDR ACC SNR; % 保存 QPSK 的结果
end
if sel==3
save R3.mat FDR ACC SNR; % 保存 QPSK 的结果
end
2174.算法理论概述
QPSK 调制原理:QPSK(四相相移键控)是一种常用的数字调制方式。它将输入的二进制比特流分成两路,分别进行正交调制。具体来说,设输入的二进制比特流为b(t),将其分为两路I(t)和Q(t),每路的比特速率是原比特流的一半。然后,用这两路信号分别对载波的同相分量和正交分量进行调制。数学表达式为:

在实际通信中,由于收发两端的载波频率可能存在偏差,会导致接收到的 QPSK 信号产生频偏。设频偏为Δω,则接收到的带频偏 QPSK 信号可以表示为:

其中n(t)是加性高斯白噪声。频偏会使 QPSK信号的相位发生线性变化,从而影响信号的检测和识别。
卷积神经网络(CNN)在图像处理和信号处理领域有着广泛的应用。对于带频偏QPSK调制信号检测识别,CNN可以自动学习信号的特征,通过卷积层提取信号的局部特征,池化层对特征进行压缩和降维,全连接层将提取的特征进行分类。CNN能够自适应地处理频偏带来的相位变化,通过大量的训练数据学习到不同频偏下QPSK信号的特征模式,从而实现准确的检测和识别。
将预处理后的数据分为训练集和验证集,使用训练集对 CNN 模型进行训练。在每次迭代中,将一批训练数据输入到模型中,计算损失函数并通过优化算法更新模型的参数。同时,在验证集上评估模型的性能,根据验证集的损失和准确率等指标来调整模型的超参数,如学习率、卷积核大小、层数等,直到模型收敛或达到预设的训练轮数。
5.算法完整程序工程
OOOOO
OOO
O