Java二叉树题目练习

相同的树

二叉树的题目大多数时候就可以采用递归的方法写
因为二叉树是由根左子树和右子树组成，每一棵左子树和右子树又可以被看成一颗完整的树，因此大事化小，小事化了

目的：就是判断两个树是完全相同
思路：采用递归的方法，因为在二叉树中树是由根、左子树和右子树组成，每一个左子树和右子树又可以被看成一颗完整的树，因此这里重要的是找好递归的截止条件就行

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //都为空的话就返回true
        if(p==null&&q==null){
            return true;
        }
        //一个为空，一个不为空的话就返回false
        if(p==null&&q!=null||p!=null&&q==null){
            return false;
        }
        //值不相同返回false
        if(p.val!=q.val){
            return false;
        }

        //两个不为空且值相同的话就继续递归
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
}

对称二叉树

class Solution {
    public boolean isSymmetric(TreeNode root) {
        //为空的话就返回true
        if(root==null){
            return true;
        }
        //利用判断是否相同的方法
        return isSymmetrichild(root.left,root.right);
    }
    public boolean isSymmetrichild(TreeNode left,TreeNode right){
        if(left==null&&right!=null||left!=null&&right==null){
            return false;
        }
        if(left==null&&right==null){
            return true;
        }
        if(left.val!=right.val){
            return false;
        }
        return isSymmetrichild(left.left,right.right)&&isSymmetrichild(left.right,right.left);
    }
}

平衡二叉树

目的：一棵树左右深度差不大于1就是平衡二叉树
这里从底到顶进行向上返回
思路：函数Height(root)来求其左子树和右子树深度差
返回值：
如果其深度差<=1：返回当前深度，
如果深度差>1就返回-1
中止条件：
root为空时候，说明找完了，返回当前高度为0
左子树/右子树深度为-1，或者深度差>1就返回-1，说明不是平衡二叉树

class Solution {
    public boolean isBalanced(TreeNode root) {
       if(root==null){
        return true;
       }
       
       return Height(root)!=-1;      
    }
    //求树的深度差
    public int Height(TreeNode root){
        if(root==null){
            return 0;
        }
        //求出左子树和右子树
        int left = Height(root.left);
        if(left<0){
            return -1;
        }
        int right = Height(root.right);
        if(right<0){
            return -1;
        }
        if(left>=0&&right>=0&&Math.abs(left-right)<=1){
             return left>right? left+1:right+1;
        }else{
            return -1;
        }
       
    }
}

如果这里不是平衡二叉树，Height函数返回-1，如果是就返回其长度
所有子在isBalanced,只要判断其返回是否是-1就行

二叉树的最近公共祖先

目的：就是一棵二叉树中的两个节点p和q，找这两个节点最近相同的公共祖先
思路：就是在root树的左子树和右子树中找p和q,注意每一颗左子树和右子树又分别是一颗完整的树
截止：找到节点或者root为null
返回值：如果left和right都不为null，那他们的祖先就是root节点
如果left != null ，返回left节点
如果right != null，返回right节点

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //1.判断是否为空
        if(root==null){
            return null;
        }
        //2.是否找到p或者q
        if(root==q||root == p){
            return root;
        }
        //3.递归左子树和右子树进行判断
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);

        if(left!=null&&right!=null){
            return root;
        }else if(left!=null){
            return left;
        }else{
            return right;
        }
    }
}

二叉树的层序遍历

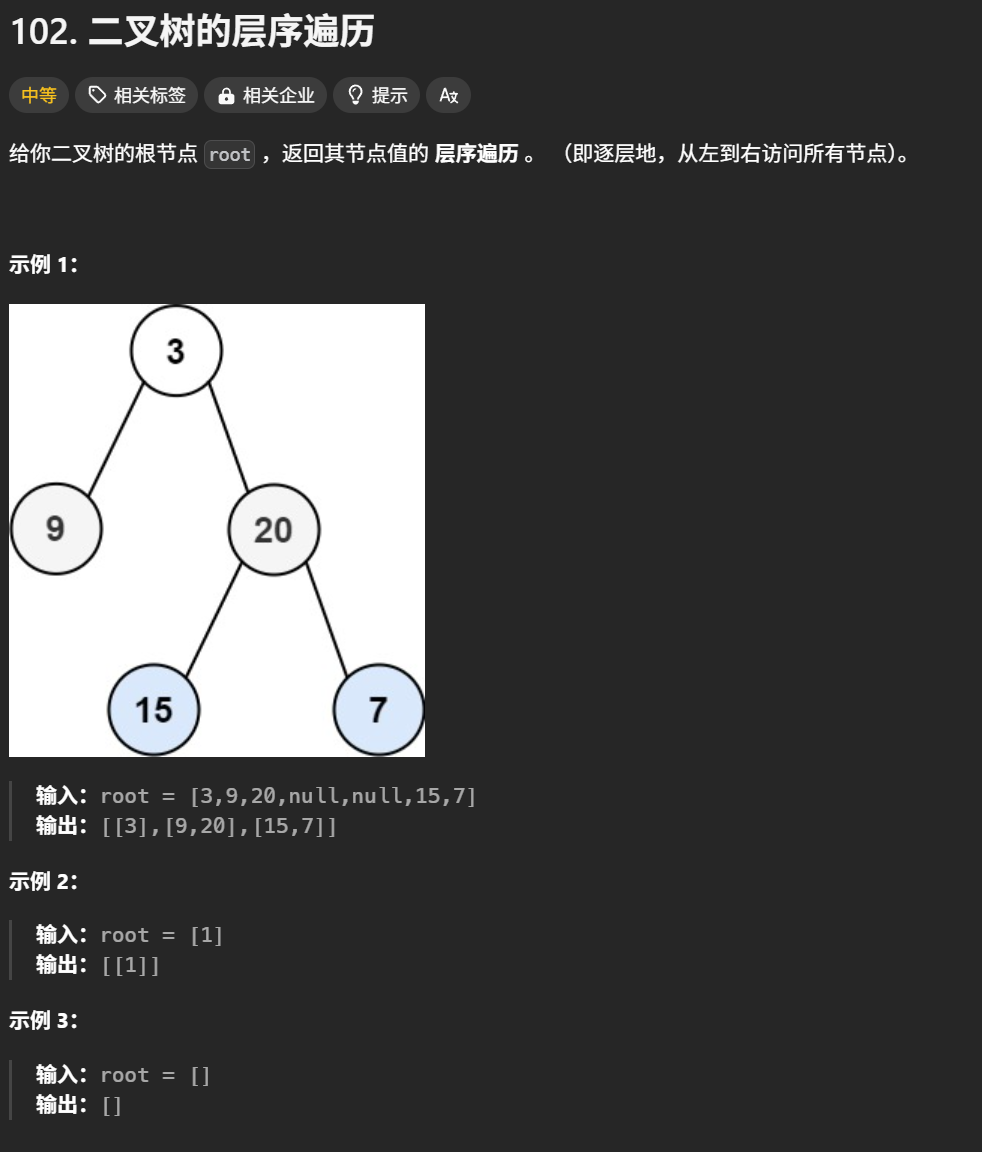
目的：就是层序输出从上到下每一层的节点，这里返回List<List< Integer >>这个二维列表
思路：二维链表就是由许多一维列表组成，确定每一行的一维链表放入二维链表中就行
这里使用Queue队列来完成存放，知道队列先入先出的原则
1.先把root节点放入队列中
2.求出队列长度，确定每一行要出多少数放入一维队列中，出队列
3.判断这个出去的节点左右子树是否为空，不为空的入队列
4.最后将一链表表放入二维链表中
5.当对列为空的时候就结束了

注意每次出队列的时候要计算其此时队列长度，这个长度就代表自己这一次要出队列元素个数

class Solution {
    public  levelOrder(TreeNode root) {
         //将其层序遍历分开行就行
        List<List<Integer>> ret = new ArrayList();
        if(root==null){
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        //先把头节点放进去
        queue.offer(root);
        while (!queue.isEmpty()){
            List<Integer> curRow = new ArrayList();
            //求队列长度确定出多少队列元素
            int size = queue.size();
           while(size!=0){
             //出队列
            TreeNode cur = queue.poll();
            curRow.add(cur.val);
            //判断出栈的这个左子树和右子树是否为空
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
            size--;
           }
           ret.add(curRow);
        }
        return ret;
    }
}

二叉树层序遍历 ||

目的：从下到上层序遍历
思路：和上面从上到下的层序遍历思路一样，就是最后一步的将一位链表放入二维链表中采用头插法，这样就会将其反过来了

class Solution {
    public  levelOrder(TreeNode root) {
         //将其层序遍历分开行就行
        List<List<Integer>> ret = new ArrayList();
        if(root==null){
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        //先把头节点放进去
        queue.offer(root);
        while (!queue.isEmpty()){
            List<Integer> curRow = new ArrayList();
            int size = queue.size();
           while(size!=0){
             //出队列
            TreeNode cur = queue.poll();
            curRow.add(cur.val);
            //判断出栈的这个左子树和右子树是否为空
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
            size--;
           }
           ret.add(curRow);
        }
        return ret;
    }
}

二叉树遍历

目的：就是给你一个前序遍历字符串(由字母和‘#’构成)，’ # '表示的是空格，并中序打印
思路：1.先输入一个字符串
2.创建这棵树
3.中序遍历打印
已知先序遍历：根-》左子树-》右子树
中序遍历：左子树-》根-》右子树

这里注意要先写构造树的类，这里创建树采用递归
因为每一棵树的左子树和右子树分别可以看成一颗完整的树
这里再递归的时候，每个节点的左子树和右子树回递归，回归的时候回将回归这两个节点链接起来

import java.util.Scanner;
//树的构造方法类
class TreeNode{
    public char val;
    public TreeNode left;
    public TreeNode right;
    
    //构造方法给其val赋值
    public TreeNode(char val){
        this.val = val;
    }
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 注意 while 处理多个 case
            //1.输入字符串
            String str = in.nextLine();
            //2.构建二叉树
            TreeNode root = creatTree(str);
            //3.中序遍历打印二叉树
            inorder(root);
        }
    }
    //确定遍历到那个字符
    public static int i = 0;
    public static TreeNode creatTree(String str){
        char ch = str.charAt(i);
        TreeNode root = null;
        if(ch!='#'){
           //将这个放入树中
           root = new TreeNode(ch);
           i++;//指向下一个
           root.left = creatTree(str);
           root.right = creatTree(str);
        }else{
            i++;
        }
        return root;
    }
    //打印
    public static void inorder(TreeNode root){
        if(root == null){
            return;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }
}