【漫话机器学习系列】266.雅可比矩阵（Jacobian Matrix）-EW帮帮网

雅可比矩阵（Jacobian Matrix）详解 | 多变量函数微积分的基石

在深度学习、计算图、优化算法、机器人控制、流形学习等众多领域中，“雅可比矩阵（Jacobian Matrix）”是一个非常核心的数学工具。

这篇文章将结合一张视觉化图示，帮助大家从零理解什么是雅可比矩阵、它的数学形式、几何含义以及实际应用场景。

一、什么是雅可比矩阵？

雅可比矩阵（Jacobian Matrix）是描述多变量向量函数的一阶偏导数矩阵。

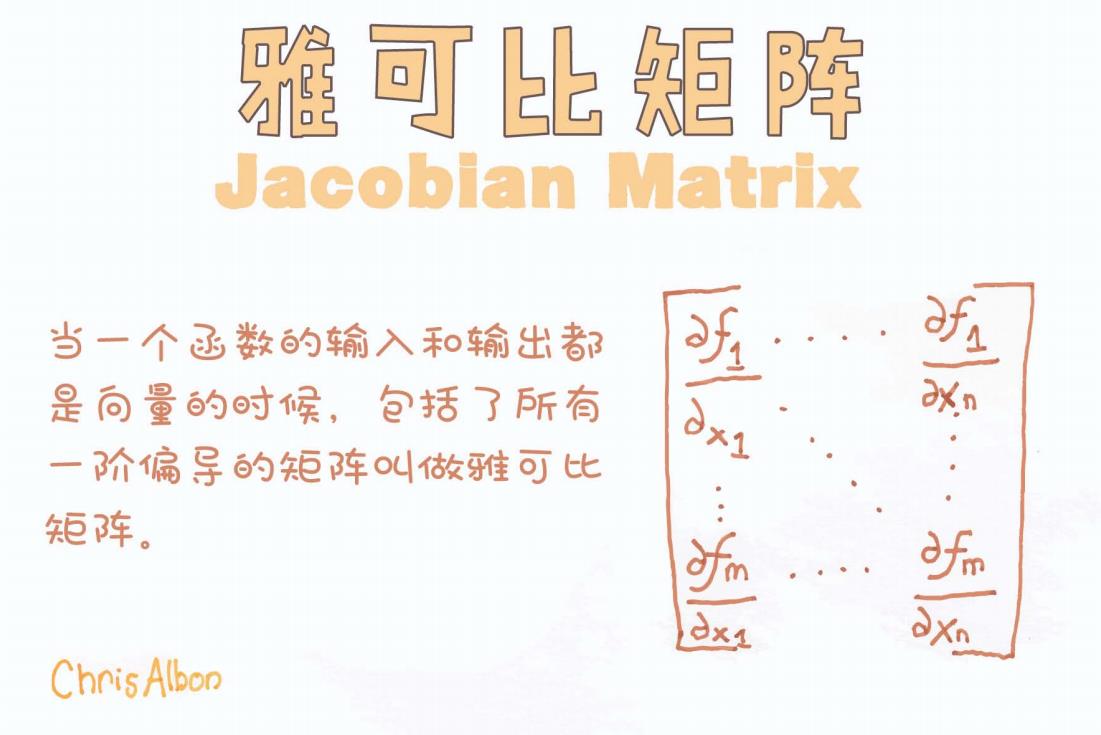
图示定义（来自 Chris Albon）：

“当一个函数的输入和输出都是向量的时候，
包括了所有一阶偏导的矩阵叫做雅可比矩阵。”

数学定义：

假设一个向量函数：

$\mathbf{f}(\mathbf{x}) = \begin{bmatrix} f_1(x_1, \dots, x_n) \\ f_2(x_1, \dots, x_n) \\ \vdots \\ f_m(x_1, \dots, x_n) \end{bmatrix}, \quad \mathbf{x} \in \mathbb{R}^n, \quad \mathbf{f} \in \mathbb{R}^m$

那么它的雅可比矩阵 $J \in \mathbb{R}^{m \times n}$ 为：

$J = \frac{\partial \mathbf{f}}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}$

二、雅可比矩阵的几何含义

雅可比矩阵可以被理解为多变量函数在某一点附近的线性近似。

在一元函数中，我们用导数表示变化率；在多元函数中，雅可比矩阵就像是“变化率”的推广：它描述了输入变量微小变化如何影响输出变量的每一维度。

举例：

在二维到二维的函数中，Jacobian 矩阵是一个 2×2 矩阵。这个矩阵可以看作是一个局部线性变换：比如一个向量场的“旋转 + 缩放”。

三、与其他微分工具的关系

工具名称	输入	输出	含义/作用
导数 (scalar)	f(x)	$\frac{df}{dx}$	单变量函数的变化率
梯度 (gradient)	f(x) $f(\mathbf{x})$	$f \in \mathbb{R}^n$	多元标量函数的一阶导数向量
雅可比矩阵 (Jacobian)	$\mathbf{f}(\mathbf{x})$	$J \in \mathbb{R}^{m \times n}$	多元向量函数的偏导数矩阵
海森矩阵 (Hessian)	$f(\mathbf{x})$	$H \in \mathbb{R}^{n \times n}$	二阶偏导矩阵（对梯度再求导）

四、应用场景

1. 神经网络中的反向传播

在反向传播过程中，我们需要计算误差函数对每一层的输入的偏导数，涉及到大量的雅可比矩阵链式相乘。

2. 自动微分（Autograd）

如 PyTorch、TensorFlow、JAX 等框架，自动微分系统内部使用雅可比矩阵或者其稀疏结构进行高效求导。

3. 非线性最小二乘优化（如 Levenberg-Marquardt 算法）

优化目标函数通常是向量形式，求解过程中需要用到雅可比矩阵作为局部线性化的基础。

4. 机器人动力学

描述机器人关节角度变化如何影响末端执行器位置（即正运动学）的函数，其一阶导数矩阵就是雅可比矩阵。

五、示意图解读（图中矩阵结构）

从图中我们可以看出，雅可比矩阵按如下结构排列：

$J = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}$

每一行对应一个输出维度（即 $f_i$ ）
每一列对应一个输入变量（即 $x_j$ ）
整个矩阵提供了对所有输入变量的灵敏度信息

六、总结

雅可比矩阵是数学、工程和 AI 世界中非常基础且强大的工具。它就像是连接输入输出之间变化关系的桥梁。

本文小结：

雅可比矩阵是多变量向量函数的一阶偏导矩阵；
它刻画了输入微小变化如何影响输出；
在神经网络、机器人、优化、微分方程中广泛使用；
它的几何含义是局部线性变换。

推荐进一步阅读：

《Numerical Optimization》—— Jorge Nocedal
《Matrix Calculus》—— Magnus & Neudecker
PyTorch 教程中关于 autograd 和 Jacobian 的介绍
Scipy 的 optimize.least_squares 官方文档

如你觉得这篇文章对你有帮助，欢迎点赞 + 收藏 + 留言讨论！
后续我将继续更新更多数学与 AI 相关的可视化知识解析。

【漫话机器学习系列】266.雅可比矩阵（Jacobian Matrix）