完整内容请看文章最下面的推广群
已更新全部思路、模型+问题一代码
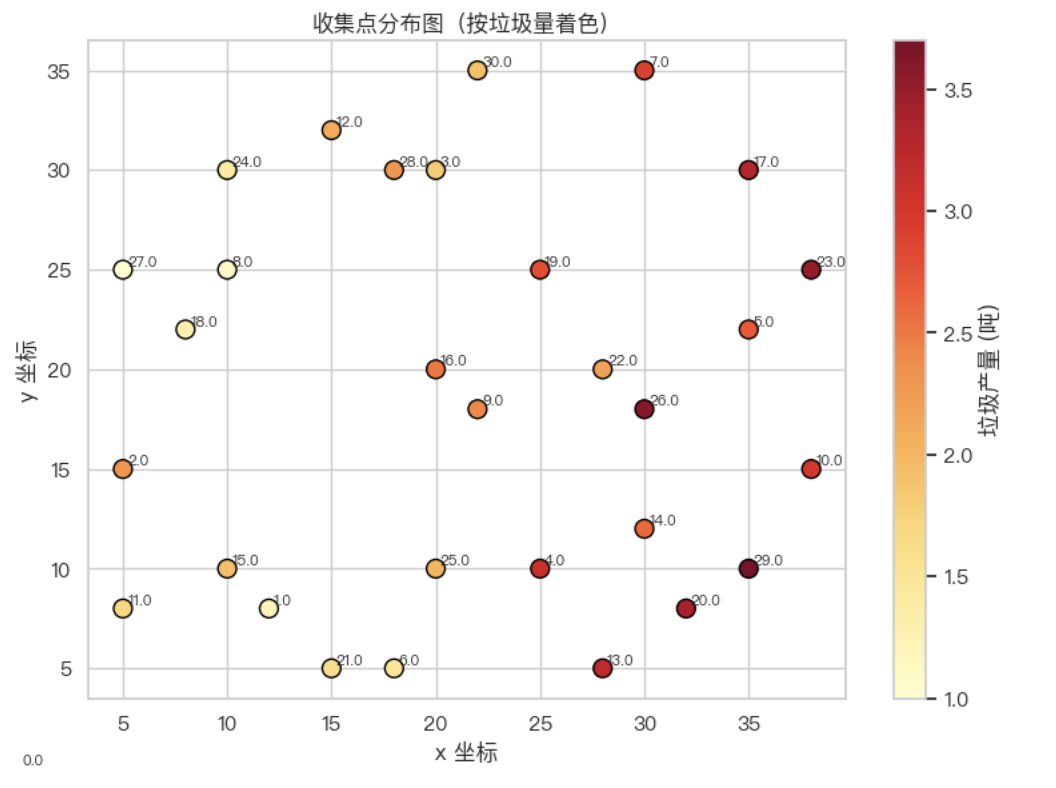


问题一:单一车辆类型下的基础路径优化与调度
本问题聚焦于最简化的垃圾运输场景:单一垃圾类型(如厨余垃圾)、单一车辆类型、单一出发/返回点(垃圾处理厂)。题目给出若干个收集点的位置坐标与每日产生垃圾的重量,同时规定运输车辆的最大载重。运输任务允许车辆多次往返,目标是在满足所有垃圾运输的前提下,使总行驶距离最小化。
建模上,这是一个带容量约束的多旅行商问题(CVRP)。决策变量包括车辆的数量、每辆车的服务路线(即访问的收集点次序)以及每趟装载的垃圾总量。模型的主要约束为:每个收集点必须被服务一次且仅一次,每趟运输不得超过车辆最大载重,所有车辆均从垃圾处理厂出发并返回。目标函数为所有车辆行驶路径的总长度最小。该问题可使用整数线性规划进行精确建模,但在实际求解中,由于问题为NP难,建议采用启发式或元启发式方法,如遗传算法、模拟退火或禁忌搜索等。模型的时间复杂度主要受车辆数与收集点数增长的组合路径影响,属于组合优化中的难解问题。

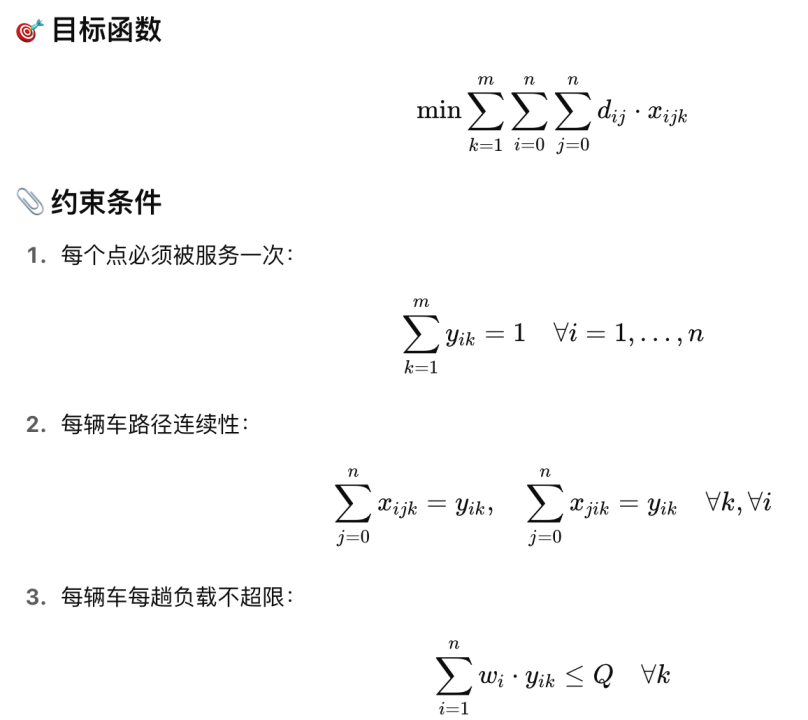
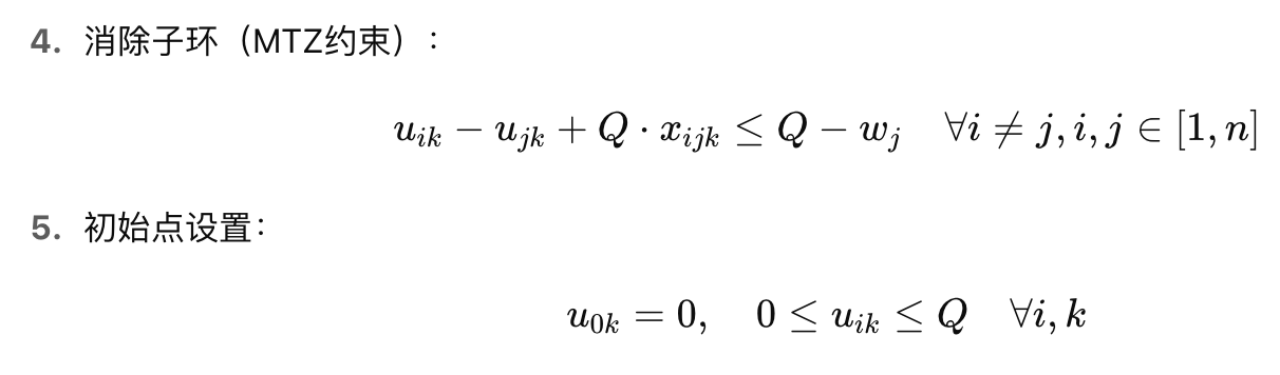
问题二:多车辆协同与载重约束下的优化
在问题一的基础上,问题二引入现实中存在的垃圾分类需求。每个收集点可能产生四种类型的垃圾(厨余、可回收、有害、其他),而每种垃圾需由专用车辆运输。不同类型车辆具有不同的载重上限、容积限制和单位运输成本。因此,调度需考虑多车辆协同、多物料分流、多目标优化的问题。
本问题可建模为多类型车辆的多旅行商路径优化问题(MTVRP),其中每类垃圾与其对应车辆类型构成一个子问题,各子问题互相独立但共享全局资源(如路径、处理厂)。每类车辆需在保证容量与容积限制的前提下收集对应垃圾类型,目标函数为每日总运输成本最小。模型中需增加变量以表示每辆车收集哪类垃圾、访问哪些收集点、运载多少垃圾等,并对运输距离与车辆使用情况加权计算运输成本。
模型还可扩展引入时间约束:若每辆车每天最多行驶一定时间(例如12小时),则必须将最大行驶距离控制在车辆速度与时间的乘积之内。这可能导致部分任务需拆分至不同车辆或不同趟次完成,对路径分配与任务调度提出新的挑战。


问题三:含中转站选址与时间窗口的综合优化
问题三进一步引入城市垃圾处理中常见的中转站机制。中转站可以分担处理厂负担、缩短路径,但带来额外的选址成本、容量限制和时间窗口约束。车辆在运输垃圾时可选择先送至中转站,后由其他车辆或批次继续送至处理厂,从而形成两级运输路径。同时,问题还引入碳排放限制,其排放量与车辆载重和行驶距离线性相关。
建模时,可构建两阶段的综合优化模型。第一阶段为中转站选址问题(Facility Location Problem),决策哪些中转站启用,以使总运输成本与建设成本之和最小。第二阶段为基于中转站的垃圾运输路径优化,可采用类似问题二的模型,需增加中转站容量约束与时间窗限制。时间窗通过限制车辆在中转站的服务时间控制收发调度,而碳排放作为辅助目标可加入多目标优化框架,或转化为约束纳入模型。
此外,中转站的选址直接影响运输路径长度与可行性,而路径规划又反过来反馈中转站的负载和使用效率,因此两个阶段需协同联动优化。例如可采用“中转站启发式 + 路径局部优化”的策略反复迭代至收敛。该问题涉及设施规划、路径优化、时间调度与碳减排多重因素,是典型的复杂城市物流问题。


本问题关注城市实际路网中存在的非对称性,如单行道、限时禁行、交通方向管制等,使得从点i到点j的距离不再等于从j到i的距离。此类路网导致原先对称假设下可用的路径优化算法(如对称TSP)失效,模型必须更新为有向图路径优化问题。
建模时需调整原始的距离矩阵,将其改为不对称的二维矩阵d(i,j) ≠ d(j,i)。此改动虽不影响基本的CVRP或MTVRP建模框架,但在算法实现上,路径搜索策略、剪枝机制和可行性判断方式必须更新,不能再依赖对称性优化。非对称网络下,路径选择变得更复杂,可能出现某些路径单向可行、反向不可行的情况,对整体运输调度策略影响较大。
在对比对称与非对称网络的路径优化复杂度时,可以发现后者路径组合更丰富、搜索空间更大,求解难度显著上升。为应对这一挑战,可采用图预处理算法(如Floyd-Warshall计算所有对最短路径),配合启发式路径构造方法(如最近插入法、路径重接)提升算法效率。
